Learning Objectives
By the end of this section, you will be able to:
- Describe energy transformations and conversions in general terms
- Explain what it means for an energy source to be renewable or nonrenewable
In this chapter, we have studied energy. We learned that energy can take different forms and can be transferred from one form to another. You will find that energy is discussed in many everyday, as well as scientific, contexts, because it is involved in all physical processes. It will also become apparent that many situations are best understood, or most easily conceptualized, by considering energy. So far, no experimental results have contradicted the conservation of energy. In fact, whenever measurements have appeared to conflict with energy conservation, new forms of energy have been discovered or recognized in accordance with this principle.
What are some other forms of energy? Many of these are covered in later chapters (also see (Figure)), but let’s detail a few here:
- Atoms and molecules inside all objects are in random motion. The internal kinetic energy from these random motions is called thermal energy, because it is related to the temperature of the object. Note that thermal energy can also be transferred from one place to another, not transformed or converted, by the familiar processes of conduction, convection, and radiation. In this case, the energy is known as heat energy.
- Electrical energy is a common form that is converted to many other forms and does work in a wide range of practical situations.
- Fuels, such as gasoline and food, have chemical energy, which is potential energy arising from their molecular structure. Chemical energy can be converted into thermal energy by reactions like oxidation. Chemical reactions can also produce electrical energy, such as in batteries. Electrical energy can, in turn, produce thermal energy and light, such as in an electric heater or a light bulb.
- Light is just one kind of electromagnetic radiation, or radiant energy, which also includes radio, infrared, ultraviolet, X-rays, and gamma rays. All bodies with thermal energy can radiate energy in electromagnetic waves.
- Nuclear energy comes from reactions and processes that convert measurable amounts of mass into energy. Nuclear energy is transformed into radiant energy in the Sun, into thermal energy in the boilers of nuclear power plants, and then into electrical energy in the generators of power plants. These and all other forms of energy can be transformed into one another and, to a certain degree, can be converted into mechanical work.
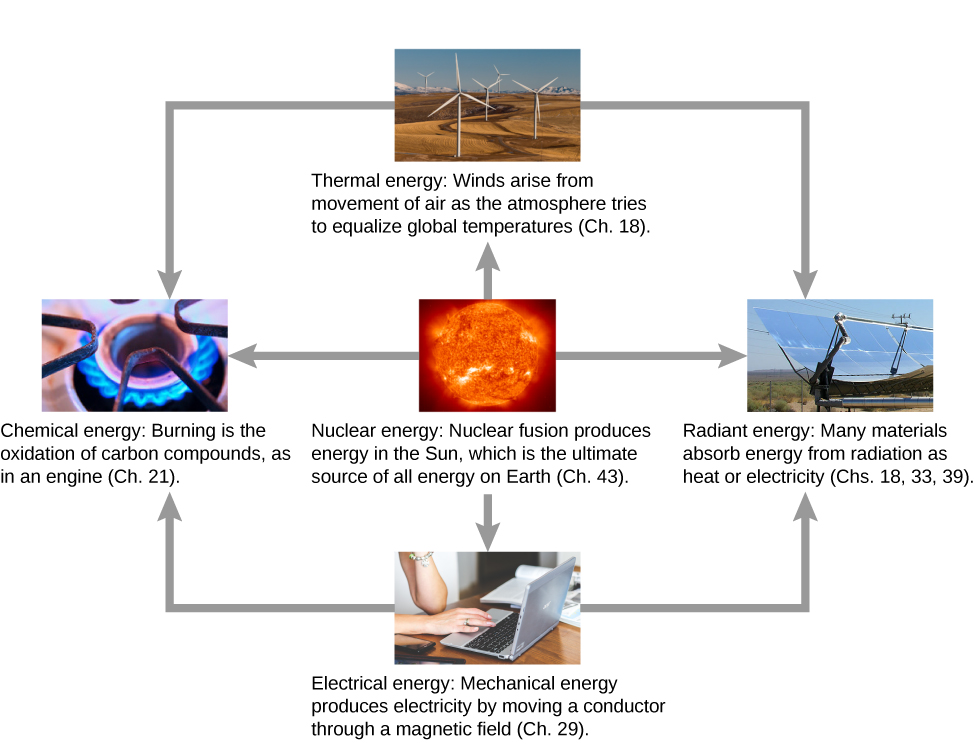
Figure 8.13 Energy that we use in society takes many forms, which be converted from one into another depending on the process involved. We will study many of these forms of energy in later chapters in this text. (credit “sun”: EIT SOHO Consortium, ESA, NASA; credit “solar panels”: “kjkolb”/Wikimedia Commons; credit “gas burner”: Steven Depolo)
The transformation of energy from one form into another happens all the time. The chemical energy in food is converted into thermal energy through metabolism; light energy is converted into chemical energy through photosynthesis. Another example of energy conversion occurs in a solar cell. Sunlight impinging on a solar cell produces electricity, which can be used to run electric motors or heat water. In an example encompassing many steps, the chemical energy contained in coal is converted into thermal energy as it burns in a furnace, to transform water into steam, in a boiler. Some of the thermal energy in the steam is then converted into mechanical energy as it expands and spins a turbine, which is connected to a generator to produce electrical energy. In these examples, not all of the initial energy is converted into the forms mentioned, because some energy is always transferred to the environment.
Energy is an important element at all levels of society. We live in a very interdependent world, and access to adequate and reliable energy resources is crucial for economic growth and for maintaining the quality of our lives. The principal energy resources used in the world are shown in (Figure). The figure distinguishes between two major types of energy sources: renewable and non-renewable, and further divides each type into a few more specific kinds. Renewable sources are energy sources that are replenished through naturally occurring, ongoing processes, on a time scale that is much shorter than the anticipated lifetime of the civilization using the source. Non-renewable sources are depleted once some of the energy they contain is extracted and converted into other kinds of energy. The natural processes by which non-renewable sources are formed typically take place over geological time scales.

Figure 8.14 World energy consumption by source; the percentage of renewables is increasing, accounting for 19% in 2012.
Our most important non-renewable energy sources are fossil fuels, such as coal, petroleum, and natural gas. These account for about 81% of the world’s energy consumption, as shown in the figure. Burning fossil fuels creates chemical reactions that transform potential energy, in the molecular structures of the reactants, into thermal energy and products. This thermal energy can be used to heat buildings or to operate steam-driven machinery. Internal combustion and jet engines convert some of the energy of rapidly expanding gases, released from burning gasoline, into mechanical work. Electrical power generation is mostly derived from transferring energy in expanding steam, via turbines, into mechanical work, which rotates coils of wire in magnetic fields to generate electricity. Nuclear energy is the other non-renewable source shown in (Figure) and supplies about 3% of the world’s consumption. Nuclear reactions release energy by transforming potential energy, in the structure of nuclei, into thermal energy, analogous to energy release in chemical reactions. The thermal energy obtained from nuclear reactions can be transferred and converted into other forms in the same ways that energy from fossil fuels are used.
An unfortunate byproduct of relying on energy produced from the combustion of fossil fuels is the release of carbon dioxide into the atmosphere and its contribution to global warming. Nuclear energy poses environmental problems as well, including the safety and disposal of nuclear waste. Besides these important consequences, reserves of non-renewable sources of energy are limited and, given the rapidly growing rate of world energy consumption, may not last for more than a few hundred years. Considerable effort is going on to develop and expand the use of renewable sources of energy, involving a significant percentage of the world’s physicists and engineers.
Four of the renewable energy sources listed in (Figure)—those using material from plants as fuel (biomass heat, ethanol, biodiesel, and biomass electricity)—involve the same types of energy transformations and conversions as just discussed for fossil and nuclear fuels. The other major types of renewable energy sources are hydropower, wind power, geothermal power, and solar power.
Hydropower is produced by converting the gravitational potential energy of falling or flowing water into kinetic energy and then into work to run electric generators or machinery. Converting the mechanical energy in ocean surface waves and tides is in development. Wind power also converts kinetic energy into work, which can be used directly to generate electricity, operate mills, and propel sailboats.
The interior of Earth has a great deal of thermal energy, part of which is left over from its original formation (gravitational potential energy converted into thermal energy) and part of which is released from radioactive minerals (a form of natural nuclear energy). It will take a very long time for this geothermal energy to escape into space, so people generally regard it as a renewable source, when actually, it’s just inexhaustible on human time scales.
The source of solar power is energy carried by the electromagnetic waves radiated by the Sun. Most of this energy is carried by visible light and infrared (heat) radiation. When suitable materials absorb electromagnetic waves, radiant energy is converted into thermal energy, which can be used to heat water, or when concentrated, to make steam and generate electricity ((Figure)). However, in another important physical process, known as the photoelectric effect, energetic radiation impinging on certain materials is directly converted into electricity. Materials that do this are called photovoltaics (PV in (Figure)). Some solar power systems use lenses or mirrors to concentrate the Sun’s rays, before converting their energy through photovoltaics, and these are qualified as CSP in (Figure).

Figure 8.15 Solar cell arrays found in a sunny area converting the solar energy into stored electrical energy. (credit: Sarah Swenty)
As we finish this chapter on energy and work, it is relevant to draw some distinctions between two sometimes misunderstood terms in the area of energy use. As we mentioned earlier, the “law of conservation of energy” is a very useful principle in analyzing physical processes. It cannot be proven from basic principles but is a very good bookkeeping device, and no exceptions have ever been found. It states that the total amount of energy in an isolated system always remains constant. Related to this principle, but remarkably different from it, is the important philosophy of energy conservation. This concept has to do with seeking to decrease the amount of energy used by an individual or group through reducing activities (e.g., turning down thermostats, diving fewer kilometers) and/or increasing conversion efficiencies in the performance of a particular task, such as developing and using more efficient room heaters, cars that have greater miles-per-gallon ratings, energy-efficient compact fluorescent lights, etc.
Since energy in an isolated system is not destroyed, created, or generated, you might wonder why we need to be concerned about our energy resources, since energy is a conserved quantity. The problem is that the final result of most energy transformations is waste heat, that is, work that has been “degraded” in the energy transformation. We will discuss this idea in more detail in the chapters on thermodynamics.
Summary
- Energy can be transferred from one system to another and transformed or converted from one type into another. Some of the basic types of energy are kinetic, potential, thermal, and electromagnetic.
- Renewable energy sources are those that are replenished by ongoing natural processes, over human time scales. Examples are wind, water, geothermal, and solar power.
- Non-renewable energy sources are those that are depleted by consumption, over human time scales. Examples are fossil fuel and nuclear power.
Key Equations
| Difference of potential energy | $$\text{Δ}{U}_{AB}={U}_{B}-{U}_{A}=\text{−}{W}_{AB}$$ |
| Potential energy with respect to zero of
potential energy at |
$${\overset{\to }{r}}_{0}\text{Δ}U=U(\overset{\to }{r})-U({\overset{\to }{r}}_{0})$$ |
| Gravitational potential energy near Earth’s surface | $$U(y)=mgy+\text{const}.$$ |
| Potential energy for an ideal spring | $$U(x)=\frac{1}{2}k{x}^{2}+\text{const}.$$ |
| Work done by conservative force over a closed path | $${W}_{\text{closed path}}=\oint {\overset{\to }{E}}_{\text{cons}}·d\overset{\to }{r}=0$$ |
| Condition for conservative force in two dimensions | $$(\frac{d{F}_{x}}{dy})=(\frac{d{F}_{y}}{dx})$$ |
| Conservative force is the negative derivative of potential energy | $${F}_{l}=-\frac{dU}{dl}$$ |
| Conservation of energy with no
non-conservative forces |
$$0={W}_{nc,AB}=\text{Δ}{(K+U)}_{AB}=\text{Δ}{E}_{AB}.$$ |
Problems
In the cartoon movie Pocahontas, Pocahontas runs to the edge of a cliff and jumps off, showcasing the fun side of her personality. (a) If she is running at 3.0 m/s before jumping off the cliff and she hits the water at the bottom of the cliff at 20.0 m/s, how high is the cliff? Assume negligible air drag in this cartoon. (b) If she jumped off the same cliff from a standstill, how fast would she be falling right before she hit the water?
In the reality television show “Amazing Race”, a contestant is firing 12-kg watermelons from a slingshot to hit targets down the field. The slingshot is pulled back 1.5 m and the watermelon is considered to be at ground level. The launch point is 0.3 m from the ground and the targets are 10 m horizontally away. Calculate the spring constant of the slingshot.
In the Back to the Future movies, a DeLorean car of mass 1230 kg travels at 88 miles per hour to venture back to the future. (a) What is the kinetic energy of the DeLorian? (b) What spring constant would be needed to stop this DeLorean in a distance of 0.1m?
In the Hunger Games movie, Katniss Everdeen fires a 0.0200-kg arrow from ground level to pierce an apple up on a stage. The spring constant of the bow is 330 N/m and she pulls the arrow back a distance of 0.55 m. The apple on the stage is 5.00 m higher than the launching point of the arrow. At what speed does the arrow (a) leave the bow? (b) strike the apple?
In a “Top Fail” video, two women run at each other and collide by hitting exercise balls together. If each woman has a mass of 50 kg, which includes the exercise ball, and one woman runs to the right at 2.0 m/s and the other is running toward her at 1.0 m/s, (a) how much total kinetic energy is there in the system? (b) If energy is conserved after the collision and each exercise ball has a mass of 2.0 kg, how fast would the balls fly off toward the camera?
In a Coyote/Road Runner cartoon clip, a spring expands quickly and sends the coyote into a rock. If the spring extended 5 m and sent the coyote of mass 20 kg to a speed of 15 m/s, (a) what is the spring constant of this spring? (b) If the coyote were sent vertically into the air with the energy given to him by the spring, how high could he go if there were no non-conservative forces?
In an iconic movie scene, Forrest Gump runs around the country. If he is running at a constant speed of 3 m/s, would it take him more or less energy to run uphill or downhill and why?
In the movie Monty Python and the Holy Grail a cow is catapulted from the top of a castle wall over to the people down below. The gravitational potential energy is set to zero at ground level. The cow is launched from a spring of spring constant $$ 1.1\,×\,{10}^{4}\,\text{N/m} $$ that is expanded 0.5 m from equilibrium. If the castle is 9.1 m tall and the mass of the cow is 110 kg, (a) what is the gravitational potential energy of the cow at the top of the castle? (b) What is the elastic spring energy of the cow before the catapult is released? (c) What is the speed of the cow right before it lands on the ground?
A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m high rise as shown. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.80.

(a) How high a hill can a car coast up (engines disengaged) if work done by friction is negligible and its initial speed is 110 km/h? (b) If, in actuality, a 750-kg car with an initial speed of 110 km/h is observed to coast up a hill to a height 22.0 m above its starting point, how much thermal energy was generated by friction? (c) What is the average force of friction if the hill has a slope of $$ 2.5\text{°} $$ above the horizontal?
A $$ 5.00\,×\,{10}^{5}\,\text{-kg} $$ subway train is brought to a stop from a speed of 0.500 m/s in 0.400 m by a large spring bumper at the end of its track. What is the spring constant k of the spring?
A pogo stick has a spring with a spring constant of $$ 2.5\,×\,{10}^{4}\,\text{N/m,} $$ which can be compressed 12.0 cm. To what maximum height from the uncompressed spring can a child jump on the stick using only the energy in the spring, if the child and stick have a total mass of 40 kg?
A block of mass 500 g is attached to a spring of spring constant 80 N/m (see the following figure). The other end of the spring is attached to a support while the mass rests on a rough surface with a coefficient of friction of 0.20 that is inclined at angle of $$ 30\text{°}. $$ The block is pushed along the surface till the spring compresses by 10 cm and is then released from rest. (a) How much potential energy was stored in the block-spring-support system when the block was just released? (b) Determine the speed of the block when it crosses the point when the spring is neither compressed nor stretched. (c) Determine the position of the block where it just comes to rest on its way up the incline.

A block of mass 200 g is attached at the end of a massless spring of spring constant 50 N/m. The other end of the spring is attached to the ceiling and the mass is released at a height considered to be where the gravitational potential energy is zero. (a) What is the net potential energy of the block at the instant the block is at the lowest point? (b) What is the net potential energy of the block at the midpoint of its descent? (c) What is the speed of the block at the midpoint of its descent?
A T-shirt cannon launches a shirt at 5.00 m/s from a platform height of 3.00 m from ground level. How fast will the shirt be traveling if it is caught by someone whose hands are (a) 1.00 m from ground level? (b) 4.00 m from ground level? Neglect air drag.
A child (32 kg) jumps up and down on a trampoline. The trampoline exerts a spring restoring force on the child with a constant of 5000 N/m. At the highest point of the bounce, the child is 1.0 m above the level surface of the trampoline. What is the compression distance of the trampoline? Neglect the bending of the legs or any transfer of energy of the child into the trampoline while jumping.
Shown below is a box of mass $$ {m}_{1} $$ that sits on a frictionless incline at an angle above the horizontal $$ \theta $$. This box is connected by a relatively massless string, over a frictionless pulley, and finally connected to a box at rest over the ledge, labeled $$ {m}_{2}$$. If $$ {m}_{1} $$ and $$ {m}_{2} $$ are a height h above the ground and $$ {m}_{2}>>{m}_{1}$$: (a) What is the initial gravitational potential energy of the system? (b) What is the final kinetic energy of the system?

Additional Problems
A massless spring with force constant $$ k=200\,\text{N/m} $$ hangs from the ceiling. A 2.0-kg block is attached to the free end of the spring and released. If the block falls 17 cm before starting back upwards, how much work is done by friction during its descent?
A particle of mass 2.0 kg moves under the influence of the force $$ F(x)=(-5{x}^{2}+7x)\,\text{N}. $$ Suppose a frictional force also acts on the particle. If the particle’s speed when it starts at $$ x=-4.0\,\text{m} $$ is 0.0 m/s and when it arrives at $$ x=4.0\,\text{m} $$ is 9.0 m/s, how much work is done on it by the frictional force between $$ x=-4.0\,\text{m} $$ and $$ x=4.0\,\text{m?}$$
Block 2 shown below slides along a frictionless table as block 1 falls. Both blocks are attached by a frictionless pulley. Find the speed of the blocks after they have each moved 2.0 m. Assume that they start at rest and that the pulley has negligible mass. Use $$ {m}_{1}=2.0\,\text{kg} $$ and $$ {m}_{2}=4.0\,\text{kg}.$$

A body of mass m and negligible size starts from rest and slides down the surface of a frictionless solid sphere of radius R. (See below.) Prove that the body leaves the sphere when $$ \theta ={\text{cos}}^{-1}(2\text{/}3).$$

A mysterious force acts on all particles along a particular line and always points towards a particular point P on the line. The magnitude of the force on a particle increases as the cube of the distance from that point; that is $$ F\infty {r}^{3}$$, if the distance from P to the position of the particle is r. Let b be the proportionality constant, and write the magnitude of the force as $$ F=b{r}^{3}$$. Find the potential energy of a particle subjected to this force when the particle is at a distance D from P, assuming the potential energy to be zero when the particle is at P.
An object of mass 10 kg is released at point A, slides to the bottom of the $$ 30\text{°} $$ incline, then collides with a horizontal massless spring, compressing it a maximum distance of 0.75 m. (See below.) The spring constant is 500 M/m, the height of the incline is 2.0 m, and the horizontal surface is frictionless. (a) What is the speed of the object at the bottom of the incline? (b) What is the work of friction on the object while it is on the incline? (c) The spring recoils and sends the object back toward the incline. What is the speed of the object when it reaches the base of the incline? (d) What vertical distance does it move back up the incline?

Shown below is a small ball of mass m attached to a string of length a. A small peg is located a distance h below the point where the string is supported. If the ball is released when the string is horizontal, show that h must be greater than 3a/5 if the ball is to swing completely around the peg.

A block leaves a frictionless inclined surfarce horizontally after dropping off by a height h. Find the horizontal distance D where it will land on the floor, in terms of h, H, and g.

A block of mass m, after sliding down a frictionless incline, strikes another block of mass M that is attached to a spring of spring constant k (see below). The blocks stick together upon impact and travel together. (a) Find the compression of the spring in terms of m, M, h, g, and k when the combination comes to rest.
Hint: The speed of the combined blocks $$ m+M\,({v}_{2}) $$ is based on the speed of block m just prior to the collision with the block M (v1) based on the equation $$ {v}_{2}=(m/m)+M\,({v}_{1})$$. This will be discussed further in the chapter on Linear Momentum and Collisions. (b) The loss of kinetic energy as a result of the bonding of the two masses upon impact is stored in the so-called binding energy of the two masses. Calculate the binding energy.

A block of mass 300 g is attached to a spring of spring constant 100 N/m. The other end of the spring is attached to a support while the block rests on a smooth horizontal table and can slide freely without any friction. The block is pushed horizontally till the spring compresses by 12 cm, and then the block is released from rest. (a) How much potential energy was stored in the block-spring support system when the block was just released? (b) Determine the speed of the block when it crosses the point when the spring is neither compressed nor stretched. (c) Determine the speed of the block when it has traveled a distance of 20 cm from where it was released.
Consider a block of mass 0.200 kg attached to a spring of spring constant 100 N/m. The block is placed on a frictionless table, and the other end of the spring is attached to the wall so that the spring is level with the table. The block is then pushed in so that the spring is compressed by 10.0 cm. Find the speed of the block as it crosses (a) the point when the spring is not stretched, (b) 5.00 cm to the left of point in (a), and (c) 5.00 cm to the right of point in (a).
A skier starts from rest and slides downhill. What will be the speed of the skier if he drops by 20 meters in vertical height? Ignore any air resistance (which will, in reality, be quite a lot), and any friction between the skis and the snow.
Repeat the preceding problem, but this time, suppose that the work done by air resistance cannot be ignored. Let the work done by the air resistance when the skier goes from A to B along the given hilly path be −2000 J. The work done by air resistance is negative since the air resistance acts in the opposite direction to the displacement. Supposing the mass of the skier is 50 kg, what is the speed of the skier at point B?
Two bodies are interacting by a conservative force. Show that the mechanical energy of an isolated system consisting of two bodies interacting with a conservative force is conserved. (Hint: Start by using Newton’s third law and the definition of work to find the work done on each body by the conservative force.)
In an amusement park, a car rolls in a track as shown below. Find the speed of the car at A, B, and C. Note that the work done by the rolling friction is zero since the displacement of the point at which the rolling friction acts on the tires is momentarily at rest and therefore has a zero displacement.

A 200-g steel ball is tied to a 2.00-m “massless” string and hung from the ceiling to make a pendulum, and then, the ball is brought to a position making a $$ 30\text{°} $$ angle with the vertical direction and released from rest. Ignoring the effects of the air resistance, find the speed of the ball when the string (a) is vertically down, (b) makes an angle of $$ 20\text{°} $$ with the vertical and (c) makes an angle of $$ 10\text{°} $$ with the vertical.
A hockey puck is shot across an ice-covered pond. Before the hockey puck was hit, the puck was at rest. After the hit, the puck has a speed of 40 m/s. The puck comes to rest after going a distance of 30 m. (a) Describe how the energy of the puck changes over time, giving the numerical values of any work or energy involved. (b) Find the magnitude of the net friction force.
A projectile of mass 2 kg is fired with a speed of 20 m/s at an angle of $$ 30\text{°} $$ with respect to the horizontal. (a) Calculate the initial total energy of the projectile given that the reference point of zero gravitational potential energy at the launch position. (b) Calculate the kinetic energy at the highest vertical position of the projectile. (c) Calculate the gravitational potential energy at the highest vertical position. (d) Calculate the maximum height that the projectile reaches. Compare this result by solving the same problem using your knowledge of projectile motion.
An artillery shell is fired at a target 200 m above the ground. When the shell is 100 m in the air, it has a speed of 100 m/s. What is its speed when it hits its target? Neglect air friction.
How much energy is lost to a dissipative drag force if a 60-kg person falls at a constant speed for 15 meters?
A box slides on a frictionless surface with a total energy of 50 J. It hits a spring and compresses the spring a distance of 25 cm from equilibrium. If the same box with the same initial energy slides on a rough surface, it only compresses the spring a distance of 15 cm, how much energy must have been lost by sliding on the rough surface?
Glossary
- non-renewable
- energy source that is not renewable, but is depleted by human consumption
- renewable
- energy source that is replenished by natural processes, over human time scales
Candela Citations
- OpenStax University Physics. Authored by: OpenStax CNX. Located at: https://cnx.org/contents/1Q9uMg_a@10.16:Gofkr9Oy@15. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.16
