5.3. Reaction coordinate diagrams

You may recall from general chemistry that it is often convenient to describe chemical reactions with energy diagrams. In an energy diagram, the vertical axis represents the overall energy of the reactants, while the horizontal axis is the ‘reaction coordinate’, tracing from left to right the progress of the reaction from starting compounds to final products. 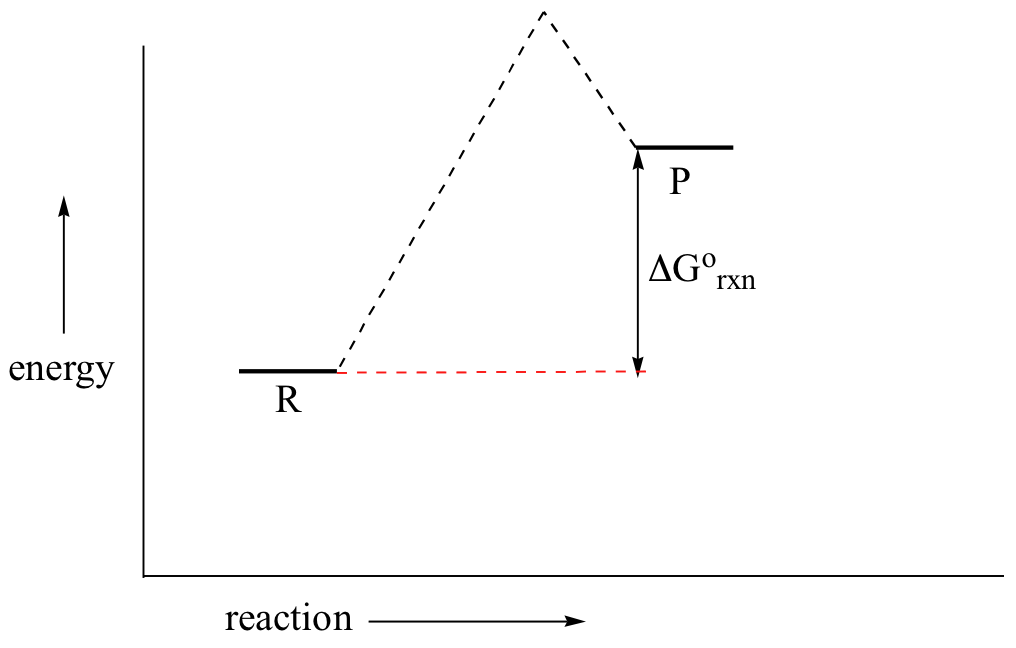The energy diagram for a typical SN2 reaction might look like this:image028.pngDespite its apparent simplicity, this energy diagram conveys some very important ideas about the thermodynamics and kinetics of the reaction. Recall that when we talk about the thermodynamics of a reaction, we are concerned with the difference in energy between reactants and products, and whether a reaction is ‘downhill’ (exergonic, energy releasing) or ‘uphill (endergonic, energy absorbing). When we talk about kinetics, on the other hand, we are concerned with the rate of the reaction, regardless of whether it is uphill or downhill thermodynamically.First,  let’s review what this energy diagram tells us about the thermodynamics of the reaction illustrated by the energy diagram above.  The energy level of the products is lower than that of the reactants. This tells us that the change in standard Gibbs Free Energy for the reaction (ΔG˚rxn) is negative.  In other words, the reaction is exergonic, or ‘downhill’. Recall that the ΔG˚rxn term encapsulates both ΔH˚rxn, the change in enthalpy (heat) and ΔS˚rxn , the change in entropy (disorder):ΔG˚ = ΔH˚- TΔS˚where T is the absolute temperature in Kelvin. For chemical processes where the entropy change is small (~0), the enthalpy change is essentially the same as the change in Gibbs Free Energy.  Energy diagrams for these processes will often plot the enthalpy (H) instead of Free Energy for simplicity.The standard Gibbs Free Energy change for a reaction can be related to the reaction’s equilibrium constant (Keq) by a simple equation:ΔG˚ = -RT ln Keq where:

  • Keq = [product] / [reactant] at equilibrium
  • R = 8.314 J×K-1×mol-1 or 1.987 cal× K-1×mol-1
  • T = temperature in Kelvin (K)

If you do the math, you see that a negative value for ΔG˚rxn (an exergonic reaction) corresponds – as it should by intuition – to Keq being greater than 1, an equilibrium constant which favors product formation.

In a hypothetical endergonic (energy-absorbing) reaction the products would have a higher energy than reactants and thus ΔG˚rxn would be positive and Keq would be less than 1, favoring reactants.

image030.png

Here is one more interesting and useful expression. Consider a simple reaction where the reactants are A and B, and the product is AB. If we know the rate constant k for the forward reaction and the rate constant kreverse for the reverse reaction (where AB splits apart into A and B), we can simply take the quotient to find our equilibrium constant Keq:

image036.png

This too should make some intuitive sense; if the forward rate constant is higher than the reverse rate constant, equilibrium should lie towards products.