Learning Outcomes
- Solve applications of percent
Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we’ll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.
Let’s start by looking at a common application of percent—tips to a server at a restaurant—to see how to set up a basic percent application.
When Aolani and her friends ate dinner at a restaurant, the bill came to [latex]\text{\$80}[/latex]. They wanted to leave a [latex]\text{20%}[/latex] tip. What amount would the tip be?
To solve this, we want to find what amount is [latex]\text{20%}[/latex] of [latex]\text{\$80}[/latex]. The [latex]\text{\$80}[/latex] is called the base. The amount of the tip would be [latex]0.20\left(80\right)[/latex], or [latex]\text{\$16}[/latex] See the image below. To find the amount of the tip, we multiplied the percent by the base.
A [latex]\text{20%}[/latex] tip for an [latex]\text{\$80}[/latex] restaurant bill comes out to [latex]\text{\$16}[/latex].
We will update the strategy we used in our earlier applications to include equations now. Notice that we will translate a sentence into an equation.
Solve an application
- Identify what you are asked to find and choose a variable to represent it.
- Write a sentence that gives the information to find it.
- Translate the sentence into an equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Write a complete sentence that answers the question.
Now that we have the strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we’ll solve involve everyday situations, you can rely on your own experience.
example
Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was [latex]\text{\$68.50}[/latex]. They want to leave an [latex]\text{18%}[/latex] tip. If the tip will be [latex]\text{18%}[/latex] of the total bill, how much should the tip be?
Solution
| What are you asked to find? | the amount of the tip |
| Choose a variable to represent it. | Let [latex]t=[/latex] amount of tip. |
| Write a sentence that give the information to find it. | The tip is 18% of the total bill. |
| Translate the sentence into an equation. |  |
| Multiply. | [latex]t=12.33[/latex] |
| Check. Is this answer reasonable? | |
| If we approximate the bill to [latex]\text{\$70}[/latex] and the percent to [latex]20\text{%}[/latex], we would have a tip of [latex]\text{\$14}[/latex].
So a tip of [latex]\text{\$12.33}[/latex] seems reasonable. |
|
| Write a complete sentence that answers the question. | The couple should leave a tip of [latex]\text{\$12.33}[/latex]. |
try it
In the next video we show another example of finding how much tip to give based on percent.
example
The label on Masao’s breakfast cereal said that one serving of cereal provides [latex]85[/latex] milligrams (mg) of potassium, which is [latex]\text{2%}[/latex] of the recommended daily amount. What is the total recommended daily amount of potassium?
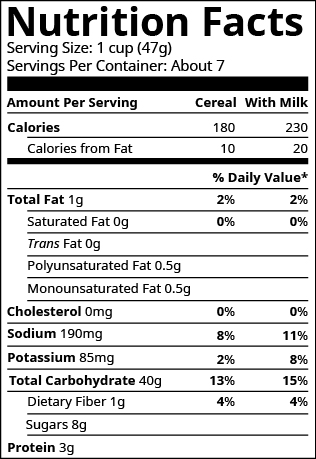
try it
example
Mitzi received some gourmet brownies as a gift. The wrapper said each brownie was [latex]480[/latex] calories, and had [latex]240[/latex] calories of fat. What percent of the total calories in each brownie comes from fat?
try it
The following video show another example of how to solve an application that involves percent.
Candela Citations
- Question ID 146703, 146702, 146701, 146697. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Percent Application - Tipping. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/yFaa2CMx9rk. License: CC BY: Attribution
- Example 1: Percent Application Problem. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/mRekG7LsUys. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757



