Learning Objectives
- Introduction to polynomial functions
- Identify polynomial functions
- Identify the degree and leading coefficient of a polynomial function
- Algebra of Polynomial Functions
-
- Add and subtract polynomial functions
- Multiply and divide polynomial functions
Identify polynomial functions
We have introduced polynomials and functions, so now we will combine these ideas to describe polynomial functions. Polynomials are algebraic expressions that are created by summing monomial terms, such as [latex]-3x^2[/latex], where the exponents are only integers. Functions are a specific type of relation in which each input value has one and only one output value. Polynomial functions have all of these characteristics as well as a domain and range, and corresponding graphs. In this section we will identify and evaluate polynomial functions. Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable.
When we introduced polynomials, we presented the following: [latex]4x^3-9x^2+6x[/latex]. We can turn this into a polynomial function by using function notation:
[latex]f(x)=4x^3-9x^2+6x[/latex]
Polynomial functions are written with the leading term first, and all other terms in descending order as a matter of convention. In the first example, we will identify some basic characteristics of polynomial functions.
Example
Which of the following are polynomial functions?
In the following video you will see additional examples of how to identify a polynomial function using the definition.
Define the degree and leading coefficient of a polynomial function
Just as we identified the degree of a polynomial, we can identify the degree of a polynomial function. To review: the degree of the polynomial is the highest power of the variable that occurs in the polynomial; the leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.
Example
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
For the function [latex]f\left(x\right)[/latex], the highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, –4.
For the function [latex]g\left(t\right)[/latex], the highest power of t is 5, so the degree is 5. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, 5.
For the function [latex]h\left(p\right)[/latex], the highest power of p is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex]; the leading coefficient is the coefficient of that term, –1.
In the next video we will show more examples of how to identify the degree, leading term and leading coefficient of a polynomial function.
Graphs of Polynomial Functions
Plotting polynomial functions using tables of values can be misleading because of some of the inherent characteristics of polynomials. Additionally, the algebra of finding points like x-intercepts for higher degree polynomials can get very messy and oftentimes impossible to find by hand. We have therefore developed some techniques for describing the general behavior of polynomial graphs.
Polynomial functions of degree 2 or more have graphs that do not have sharp corners these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. The figure below shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.
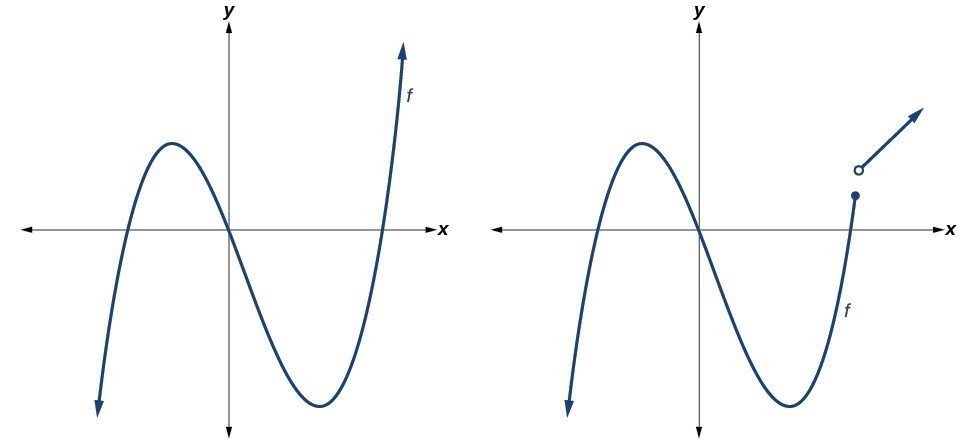
Now you try it.
Example
Which of the graphs below represents a polynomial function?
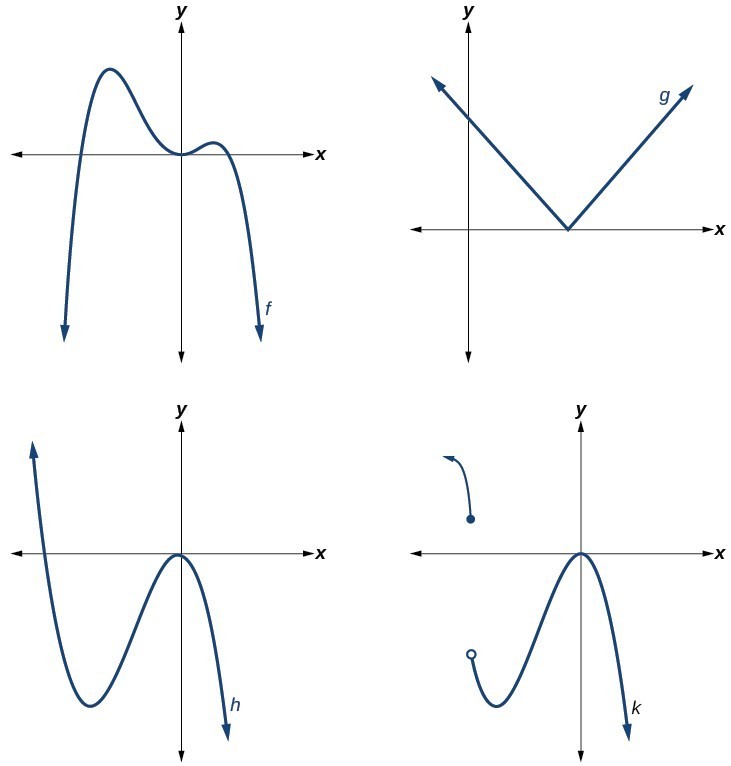
Q & A
Do all polynomial functions have as their domain all real numbers?
Yes. Any real number is a valid input for a polynomial function.
Identifying the shape of the graph of a polynomial function
Knowing the degree of a polynomial function is useful in helping us predict what it’s graph will look like. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the graph of the polynomial will match the end behavior of the term of highest degree.
As an example we compare the outputs of a degree 2 polynomial and a degree 5 polynomial in the following table.
| x | [latex]f(x)=2x^2-2x+4[/latex] | [latex]g(x)=x^5+2x^3-12x+3[/latex] |
| 1 | 4 | 8 |
| 10 | 184 | 98117 |
| 100 | 19804 | 9998001197 |
| 1000 | 1998004 | 9999980000000000 |
As the inputs for both functions get larger, the degree 5 polynomial outputs get much larger than the degree 2 polynomial outputs. This is why we use the leading term to get a rough idea of the behavior of polynomial graphs.
There are two other important features of polynomials that influence the shape of it’s graph. The first is whether the degree is even or odd, and the second is whether the leading term is negative.
Even degree polynomials
In the figure below, we show the graphs of [latex]f\left(x\right)={x}^{2},g\left(x\right)={x}^{4}[/latex] and [latex]\text{and}h\left(x\right)={x}^{6}[/latex], which are all have even degrees. Notice that these graphs have similar shapes, very much like that of a quadratic function. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.

Odd degree polynomials
The next figure shows the graphs of [latex]f\left(x\right)={x}^{3},g\left(x\right)={x}^{5},\text{and}h\left(x\right)={x}^{7}[/latex], which are all odd degree functions. 
Notice that one arm of the graph points down and the other points up. This is because when your input is negative, you will get a negative output if the degree is odd. The following table of values shows this.
| x | [latex]f(x)=x^4[/latex] | [latex]h(x)=x^5[/latex] |
| -1 | 1 | -1 |
| -2 | 16 | -32 |
| -3 | 81 | -243 |
Now you try it.
Example
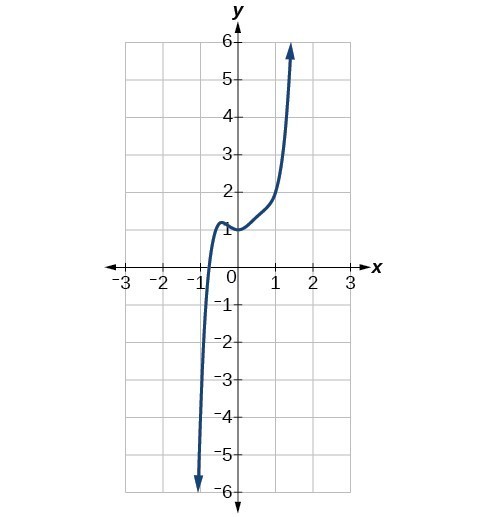
Identify whether graph represents a polynomial function that has a degree that is even or odd.
a)

b)
The sign of the leading term
What would happen if we change the sign of the leading term of an even degree polynomial? For example, let’s say that the leading term of a polynomial is [latex]-3x^4[/latex]. We will use a table of values to compare the outputs for a polynomial with leading term [latex]-3x^4[/latex], and [latex]3x^4[/latex].
| x | [latex]-3x^4[/latex] | [latex]3x^4[/latex] |
| -2 | -48 | 48 |
| -1 | -3 | 3 |
| 0 | 0 | 0 |
| 1 | -3 | 3 |
| 2 | -48 | 48 |
Plotting these points on a grid leads to this plot, the red points indicate a negative leading coefficient, and the blue points indicate a positive leading coefficient:

The negative sign creates a reflection of [latex]3x^4[/latex] across the x-axis. The arms of a polynomial with a leading term of [latex]-3x^4[/latex] will point down, whereas the arms of a polynomial with leading term [latex]3x^4[/latex] will point up.
Now you try it.
Example
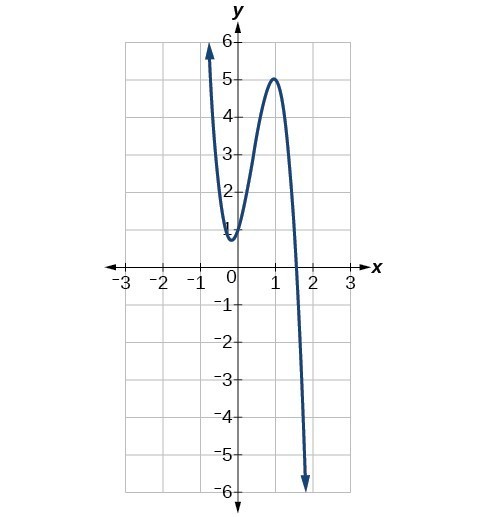
Identify whether the leading term is positive or negative and whether the degree is even or odd for the following graphs of polynomial functions.
a)

b)
Learning Objectives
- Add and subtract polynomial functions
- Multiply and divide polynomial functions
Just as we have performed algebraic operations on polynomials, we can do the same with polynomial functions. In this section we will show you how to perform algebraic operations on polynomial functions and introduce related notation.
The four basic operations on functions are adding, subtracting, multiplying, and dividing. The notation for these functions is as follows.
Addition [latex](f + g)(x) = f(x)+ g(x)[/latex]
Subtraction [latex](f − g)(x)= f(x) − g(x)[/latex]
Multiplication [latex](f · g)(x)= f(x)g(x)[/latex]
Division [latex]\frac{f}{ g} (x) = \frac{f(x)}{g(x)}[/latex]
We will focus on applying these operations to polynomial functions in this section.
Add and subtract polynomial functions
Adding and subtracting polynomial functions is the same as adding and subtracting polynomials. When you evaluate a sum or difference of functions, you can either evaluate first, or perform the operation on the functions first, as we will see. Our next examples describe the notation used to add and subtract polynomial functions.
Example
For [latex]f(x)=2x^3-5x+3[/latex] and [latex]h(x)=x-5[/latex],
Find the following:
[latex](f+h)(x)[/latex] and [latex](h-f)(x)[/latex]
In our next example we will evaluate a sum and difference of functions and show that you can get to the same result in one of two ways.
Example
For [latex]f(x)=2x^3-5x+3[/latex] and [latex]h(x)=x-5[/latex]
Evaluate: [latex](f+h)(2)[/latex]
Show that you get the same result by
1)evaluating the functions first, then performing the indicated operation on the result and
2) performing the operation on the functions first, then evaluating the result
Multiply and divide polynomial functions
We saw that multiplying polynomials often required the use of the distributive property, and that the algebra of dividing polynomials could get messy fast! The same techniques can be used to multiply and divide polynomial functions. Additionally, the same idea applies to evaluating a product or quotient of functions as we discovered in the previous example. We can either evaluate the function and then perform the indicated operation, or vice-versa. You may already be thinking – it will be a lot less work to evaluate the polynomials and then divide the results!
Example
Given: [latex]g(t)=2t^3-t^2+7[/latex] and [latex]f(t)=5t^2-3[/latex]
Find: [latex](g · f)(t)[/latex], and evaluate [latex](g · f)(-1)[/latex]
In the next example we will divide polynomial functions and then evaluate the new function.
Example
Given [latex]p(x)=2x^2+x-15[/latex] and [latex]r(x)=x+3[/latex]
Find [latex]\frac{p}{r}(x)[/latex] and evaluate [latex]\frac{p}{r}(2)[/latex]
Summary
Polynomial functions contain powers that are non-negative integers and the coefficients are real numbers. it is often helpful to know how to identify the degree and leading coefficient of a polynomial function. To do this, follow these suggestions:
- Find the highest power of x to determine the degree function.
- Identify the term containing the highest power of x to find the leading term.
- Identify the coefficient of the leading term.
Candela Citations
- Determine if a Function is a Polynomial Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/w02qTLrJYiQ. License: CC BY: Attribution
- Degree, Leading Term, and Leading Coefficient of a Polynomial Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/F_G_w82s0QA. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay, et al. Provided by: Open Stax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution. License Terms: Download fro free at : http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
