As attractive as the concept of sustainability may be as a means of framing our thoughts and goals, its definition is rather broad and difficult to work with when confronted with choices among specific courses of action. The Chapter Problem-Solving, Metrics, and Tools for Sustainability is devoted to various ways of measuring progress toward achieving sustainable goals, but here we introduce one general way to begin to apply sustainability concepts: the IPAT equation.
As is the case for any equation, IPAT expresses a balance among interacting factors. It can be stated as
where I represents the impacts of a given course of action on the environment, P is the relevant human population for the problem at hand, A is the level of consumption per person, and T is impact per unit of consumption. Impact per unit of consumption is a general term for technology, interpreted in its broadest sense as any human-created invention, system, or organization that serves to either worsen or uncouple consumption from impact. The equation is not meant to be mathematically rigorous; rather it provides a way of organizing information for a “first-order” analysis.
Suppose we wish to project future needs for maintaining global environmental quality at present day levels for the mid-twenty-first century. For this we need to have some projection of human population (P) and an idea of rates of growth in consumption (A).
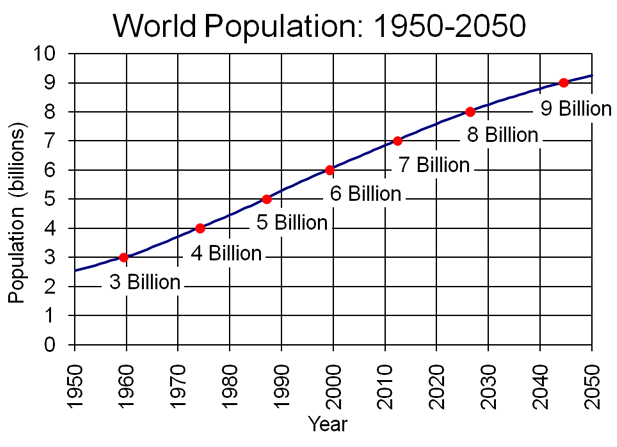
World Population Growth Source: U.S. Census Bureau, International Data Base, December 2010 Update
Figure World Population Growth suggests that global population in 2050 will grow from the current 6.8 billion to about 9.2 billion, an increase of 35%. Global GDP (Gross Domestic Product, one measure of consumption) varies from year to year but, using Figure Worldwide Growth of Gross Domestic Product as a guide, an annual growth rate of about 3.5% seems historically accurate (growth at 3.5%, when compounded for forty years, means that the global economy will be four times as large at mid-century as today).
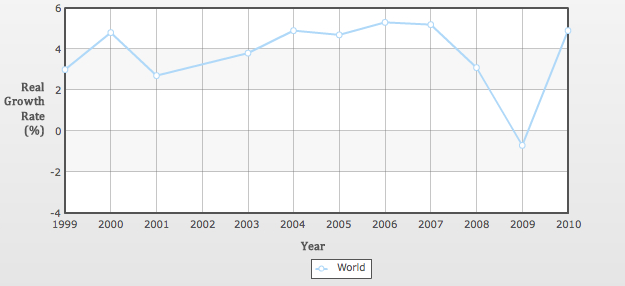
Worldwide Growth of Gross Domestic Product Source: CIA World Factbook, Graph from IndexMundi
Thus if we wish to maintain environmental impacts (I) at their current levels (i.e. I2050 = I2010), then
or
This means that just to maintain current environmental quality in the face of growing population and levels of affluence, our technological decoupling will need to reduce impacts by about a factor of five. So, for instance, many recently adopted “climate action plans” for local regions and municipalities, such as the Chicago Climate Action Plan, typically call for a reduction in greenhouse gas emissions (admittedly just one impact measure) of eighty percent by mid-century. The means to achieve such reductions, or even whether or not they are necessary, are matters of intense debate; where one group sees expensive remedies with little demonstrable return, another sees opportunities for investment in new technologies, businesses, and employment sectors, with collateral improvements in global and national well-being.
