Learning Objectives
- Introduction to Roots
- Define and evaluate principal square roots
- Define and evaluate nth roots
- Estimate roots that are not perfect
- Radical Expressions and Rational Exponents
- Define and identify a radical expression
- Convert radicals to expressions with rational exponents
- Convert expressions with rational exponents to their radical equivalent
- Simplify Radical Expressions
- Simplify radical expressions using factoring
- Simplify radical expressions using rational exponents and the laws of exponents
- Define [latex]\sqrt{x^2}=|x|[/latex], and apply it when simplifying radical expressions
Did you know that you can take the 6th root of a number? You have probably heard of a square root, written [latex]\sqrt{}[/latex], but you can also take a third, fourth and even a 5,000th root (if you really had to). In this lesson we will learn how a square root is defined and then we will build on that to form an understanding of nth roots. We will use factoring and rules for exponents to simplify mathematical expressions that contain roots.
The most common root is the square root. First, we will define what square roots are, and how you find the square root of a number. Then we will apply similar ideas to define and evaluate nth roots.
Roots are the inverse of exponents, much like multiplication is the inverse of division. Recall how exponents are defined, and written; with an exponent, as words, and as repeated multiplication.
Exponent: [latex]{{3}^{2}}[/latex], [latex]{{4}^{5}}[/latex], [latex]{{x}^{3}}[/latex], [latex]{{x}^{\text{n}}}[/latex]
Name: “Three squared” or “Three to the second power”, “Four to the fifth power”, “x cubed”, “x to the nth power”
Repeated Multiplication: [latex]3\cdot 3[/latex], [latex]4\cdot 4\cdot 4\cdot 4\cdot 4[/latex], [latex]x\cdot x\cdot x[/latex], [latex]\underbrace{x\cdot x\cdot x...\cdot x}_{n\text{ times}}[/latex].
Conversely, when you are trying to find the square root of a number (say, 25), you are trying to find a number that can be multiplied by itself to create that original number. In the case of 25, you can find that [latex]5\cdot5=25[/latex], so 5 must be the square root.
Square Roots
The symbol for the square root is called a radical symbol and looks like this: [latex]\sqrt{\,\,\,}[/latex]. The expression [latex]\sqrt{25}[/latex] is read “the square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand.
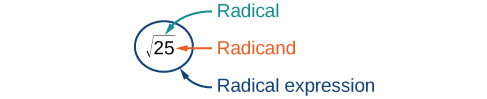
The following table shows different radicals and their equivalent written and simplified forms.
| Radical | Name | Simplified Form |
|---|---|---|
| [latex]\sqrt{36}[/latex] |
“Square root of thirty-six” “Radical thirty-six” |
[latex]\sqrt{36}=\sqrt{6\cdot 6}=6[/latex] |
| [latex]\sqrt{100}[/latex] |
“Square root of one hundred” “Radical one hundred” |
[latex]\sqrt{100}=\sqrt{10\cdot 10}=10[/latex] |
| [latex]\sqrt{225}[/latex] |
“Square root of two hundred twenty-five” “Radical two hundred twenty-five” |
[latex]\sqrt{225}=\sqrt{15\cdot 15}=15[/latex] |
Consider [latex]\sqrt{25}[/latex] again. You may realize that there is another value that, when multiplied by itself, also results in 25. That number is [latex]−5[/latex].
[latex]\begin{array}{r}5\cdot 5=25\\-5\cdot -5=25\end{array}[/latex]
By definition, the square root symbol always means to find the positive root, called the principal root. So while [latex]5\cdot5[/latex] and [latex]−5\cdot−5[/latex] both equal 25, only 5 is the principal root. You should also know that zero is special because it has only one square root: itself (since [latex]0\cdot0=0[/latex]).
In our first example we will show you how to use radical notation to evaluate principal square roots.
Example
Find the principal root of each expression.
- [latex]\sqrt{100}[/latex]
- [latex]\sqrt{16}[/latex]
- [latex]\sqrt{25+144}[/latex]
- [latex]\sqrt{49}-\sqrt{81}\\[/latex]
- [latex]-\sqrt{81}[/latex]
- [latex]\sqrt{-9}[/latex]
In the following video we present more examples of how to find a principle square root.
The last example we showed leads to an important characteristic of square roots. You can only take the square root of values that are nonnegative.
Domain of a Square Root
[latex]\sqrt{-a}[/latex] is not defined for all real numbers, a. Therefore, [latex]\sqrt{a}[/latex] is defined for [latex]a\ge0[/latex]
Think About It
Does [latex]\sqrt{25}=\pm 5[/latex]? Write your ideas and a sentence to defend them in the box below before you look at the answer.
Cube Roots
We know that [latex]5^2=25, \text{ and }\sqrt{25}=5[/latex] but what if we want to “undo” [latex]5^3=125, \text{ or }5^4=625[/latex]? We can use higher order roots to answer these questions.
Suppose we know that [latex]{a}^{3}=8[/latex]. We want to find what number raised to the 3rd power is equal to 8. Since [latex]{2}^{3}=8[/latex], we say that 2 is the cube root of 8. In the next example we will evaluate the cube roots of some perfect cubes.
Example
Evaluate the following:
- [latex]\sqrt[3]{125}[/latex]
- [latex]\sqrt[3]{-8}[/latex]
- [latex]\sqrt[3]{27}[/latex]
As we saw in the last example,there is one interesting fact about cube roots that is not true of square roots. Negative numbers can’t have real number square roots, but negative numbers can have real number cube roots! What is the cube root of [latex]−8[/latex]? [latex]\sqrt[3]{-8}=-2[/latex] because [latex]-2\cdot -2\cdot -2=-8[/latex]. Remember, when you are multiplying an odd number of negative numbers, the result is negative! Consider [latex]\sqrt[3]{{{(-1)}^{3}}}=-1[/latex].
In the following video we show more examples of finding a cube root.
Nth Roots
The cube root of a number is written with a small number 3, called the index, just outside and above the radical symbol. It looks like [latex]\sqrt[3]{{}}[/latex]. This little 3 distinguishes cube roots from square roots which are written without a small number outside and above the radical symbol.
We can apply the same idea to any exponent and it’s corresponding root. The nth root of [latex]a[/latex] is a number that, when raised to the nth power, gives [latex]a[/latex]. For example, [latex]3[/latex] is the 5th root of [latex]243[/latex] because [latex]{\left(3\right)}^{5}=243[/latex]. If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex] is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex].
The principal nth root of [latex]a[/latex] is written as [latex]\sqrt[n]{a}[/latex], where [latex]n[/latex] is a positive integer greater than or equal to 2. In the radical expression, [latex]n[/latex] is called the index of the radical.
Definition: Principal nth Root
If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex], written as [latex]\sqrt[n]{a}[/latex], is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex]. The index of the radical is [latex]n[/latex].
Example
Evaluate each of the following:
- [latex]\sqrt[5]{-32}[/latex]
- [latex]\sqrt[4]{81}[/latex]
- [latex]\sqrt[8]{-1}[/latex]
In the following video we show more examples of how to evaluate and nth root.
You can find the odd root of a negative number, but you cannot find the even root of a negative number. This means you can evaluate the radicals [latex]\sqrt[3]{-81},\ \sqrt[5]{-64}[/latex], and [latex]\sqrt[7]{-2187}[/latex], but you cannot evaluate the radicals [latex]\sqrt[{}]{-100},\ \sqrt[4]{-16}[/latex], or [latex]\sqrt[6]{-2,500}[/latex].
Estimate Roots
An approach to handling roots that are not perfect (squares, cubes, etc.) is to approximate them by comparing the values to perfect squares, cubes, or nth roots. Suppose you wanted to know the square root of 17. Let’s look at how you might approximate it.
Example
Estimate. [latex]\sqrt{17}[/latex]
This approximation is pretty close. If you kept using this trial and error strategy you could continue to find the square root to the thousandths, ten-thousandths, and hundred-thousandths places, but eventually it would become too tedious to do by hand.
For this reason, when you need to find a more precise approximation of a square root, you should use a calculator. Most calculators have a square root key [latex](\sqrt{{}})[/latex] that will give you the square root approximation quickly. On a simple 4-function calculator, you would likely key in the number that you want to take the square root of and then press the square root key.
Try to find [latex]\sqrt{17}[/latex] using your calculator. Note that you will not be able to get an “exact” answer because [latex]\sqrt{17}[/latex] is an irrational number, a number that cannot be expressed as a fraction, and the decimal never terminates or repeats. To nine decimal positions, [latex]\sqrt{17}[/latex] is approximated as 4.123105626. A calculator can save a lot of time and yield a more precise square root when you are dealing with numbers that aren’t perfect squares.
Example
Approximate [latex]\sqrt[3]{30}[/latex] and also find its value using a calculator.
The following video shows another example of how to estimate a square root.
Radical Expressions and Rational Exponents
Square roots are most often written using a radical sign, like this, [latex]\sqrt{4}[/latex]. But there is another way to represent them. You can use rational exponents instead of a radical. A rational exponent is an exponent that is a fraction. For example, [latex]\sqrt{4}[/latex] can be written as [latex]{{4}^{\tfrac{1}{2}}}[/latex].
Can’t imagine raising a number to a rational exponent? They may be hard to get used to, but rational exponents can actually help simplify some problems. Writing radicals with rational exponents will come in handy when we discuss techniques for simplifying more complex radical expressions.
Radical expressions are expressions that contain radicals. Radical expressions come in many forms, from simple and familiar, such as[latex]\sqrt{16}[/latex], to quite complicated, as in [latex]\sqrt[3]{250{{x}^{4}}y}[/latex]
Write an expression with a rational exponent as a radical
Radicals and fractional exponents are alternate ways of expressing the same thing. In the table below we show equivalent ways to express radicals: with a root, with a rational exponent, and as a principal root.
|
Radical Form |
Exponent Form |
Principal Root |
|---|---|---|
| [latex]\sqrt{16}[/latex] | [latex]{{16}^{\tfrac{1}{2}}}[/latex] | 4 |
| [latex]\sqrt{25}[/latex] | [latex]{{25}^{\tfrac{1}{2}}}[/latex] | 5 |
| [latex]\sqrt{100}[/latex] | [latex]{{100}^{\tfrac{1}{2}}}[/latex] | 10 |
Let’s look at some more examples, but this time with cube roots. Remember, cubing a number raises it to the power of three. Notice that in the examples in the table below, the denominator of the rational exponent is the number 3.
|
Radical Form |
Exponent Form |
Principal Root |
|---|---|---|
| [latex]\sqrt[3]{8}[/latex] | [latex]{{8}^{\tfrac{1}{3}}}[/latex] | 2 |
| [latex]\sqrt[3]{8}[/latex] | [latex]{{125}^{\tfrac{1}{3}}}[/latex] | 5 |
| [latex]\sqrt[3]{1000}[/latex] | [latex]{{1000}^{\tfrac{1}{3}}}[/latex] | 10 |
These examples help us model a relationship between radicals and rational exponents: namely, that the nth root of a number can be written as either [latex]\sqrt[n]{x}[/latex] or [latex]{{x}^{\frac{1}{n}}}[/latex].
|
Radical Form |
Exponent Form |
|---|---|
| [latex]\sqrt{x}[/latex] | [latex]{{x}^{\tfrac{1}{2}}}[/latex] |
| [latex]\sqrt[3]{x}[/latex] | [latex]{{x}^{\tfrac{1}{3}}}[/latex] |
| [latex]\sqrt[4]{x}[/latex] | [latex]{{x}^{\tfrac{1}{4}}}[/latex] |
| … | … |
| [latex]\sqrt[n]{x}[/latex] | [latex]{{x}^{\tfrac{1}{n}}}[/latex] |
In the table above, notice how the denominator of the rational exponent determines the index of the root. So, an exponent of [latex]\frac{1}{2}[/latex] translates to the square root, an exponent of [latex]\frac{1}{5}[/latex] translates to the fifth root or [latex]\sqrt[5]{{}}[/latex], and [latex]\frac{1}{8}[/latex] translates to the eighth root or [latex]\sqrt[8]{{}}[/latex].
Example
Express [latex]{{(2x)}^{^{\frac{1}{3}}}}[/latex] in radical form.
Remember that exponents only refer to the quantity immediately to their left unless a grouping symbol is used. The example below looks very similar to the previous example with one important difference—there are no parentheses! Look what happens.
Example
Express [latex]2{{x}^{^{\frac{1}{3}}}}[/latex] in radical form.
Write a radical expression as an expression with a rational exponent

Flexibility
We can write radicals with rational exponents, and as we will see when we simplify more complex radical expressions, this can make things easier. Having different ways to express and write algebraic expressions allows us to have flexibility in solving and simplifying them. It is like having a thesaurus when you write, you want to have options for expressing yourself!
Example
Write [latex]\sqrt[4]{81}[/latex] as an expression with a rational exponent.
Example
Express [latex]4\sqrt[3]{xy}[/latex] with rational exponents.
Rational exponents whose numerator is not equal to one
All of the numerators for the fractional exponents in the examples above were 1. You can use fractional exponents that have numerators other than 1 to express roots, as shown below.
|
Radical |
Exponent |
|---|---|
| [latex]\sqrt{9}[/latex] | [latex]9^{\frac{1}{2}}[/latex] |
| [latex]\sqrt[3]{{{9}^{2}}}[/latex] | [latex]9^{\frac{2}{3}}[/latex] |
| [latex]\sqrt[4]{9^{3}}[/latex] | [latex]9^{\frac{3}{4}}[/latex] |
| [latex]\sqrt[5]{9^{2}}[/latex] | [latex]9^{\frac{2}{5}}[/latex] |
| … | … |
| [latex]\sqrt[n]{9^{x}}[/latex] | [latex]9\frac{x}{n}[/latex] |
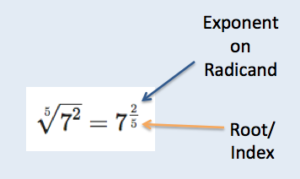
To rewrite a radical using a fractional exponent, the power to which the radicand is raised becomes the numerator and the root/ index becomes the denominator.
Writing Rational Exponents
Any radical in the form [latex]\sqrt[n]{a^{x}}[/latex] can be written using a fractional exponent in the form [latex]a^{\frac{x}{n}}[/latex].
The relationship between [latex]\sqrt[n]{{{a}^{x}}}[/latex]and [latex]{{a}^{\frac{x}{n}}}[/latex] works for rational exponents that have a numerator of 1 as well. For example, the radical [latex]\sqrt[3]{8}[/latex] can also be written as [latex]\sqrt[3]{{{8}^{1}}}[/latex], since any number remains the same value if it is raised to the first power. You can now see where the numerator of 1 comes from in the equivalent form of [latex]{{8}^{\frac{1}{3}}}[/latex].
In the next example, we practice writing radicals with rational exponents where the numerator is not equal to one.
Example
Rewrite the radicals using a rational exponent, then simplify your result.
- [latex]\sqrt[3]{{{a}^{6}}}[/latex]
- [latex]\sqrt[12]{16^3}[/latex]
In our last example we will rewrite expressions with rational exponents as radicals. This practice will help us when we simplify more complicated radical expressions, and as we learn how to solve radical equations. Typically it is easier to simplify when we use rational exponents, but this exercise is intended to help you understand how the numerator and denominator of the exponent are the exponent of a radicand and index of a radical.
Example
Rewrite the expressions using a radical.
- [latex]{x}^{\frac{2}{3}}[/latex]
- [latex]{5}^{\frac{4}{7}}[/latex]
In the following video we show more examples of writing radical expressions with rational exponents and expressions with rational exponents as radical expressions.
We will use this notation later, so come back for practice if you forget how to write a radical with a rational exponent.
Simplify Radical Expressions
Radical expressions are expressions that contain radicals. Radical expressions come in many forms, from simple and familiar, such as[latex]\sqrt{16}[/latex], to quite complicated, as in [latex]\sqrt[3]{250{{x}^{4}}y}[/latex].
To simplify complicated radical expressions, we can use some definitions and rules from simplifying exponents. Recall the Product Raised to a Power Rule from when you studied exponents. This rule states that the product of two or more non-zero numbers raised to a power is equal to the product of each number raised to the same power. In math terms, it is written [latex]\left(ab\right)^{x}=a^{x}\cdot{b}^{x}[/latex]. So, for example, you can use the rule to rewrite [latex]{{\left( 3x \right)}^{2}}[/latex] as [latex]{{3}^{2}}\cdot {{x}^{2}}=9\cdot {{x}^{2}}=9{{x}^{2}}[/latex].
Now instead of using the exponent 2, let’s use the exponent [latex]\frac{1}{2}[/latex]. The exponent is distributed in the same way.
[latex]{{\left( 3x \right)}^{\frac{1}{2}}}={{3}^{\frac{1}{2}}}\cdot {{x}^{\frac{1}{2}}}[/latex]
And since you know that raising a number to the [latex]\frac{1}{2}[/latex] power is the same as taking the square root of that number, you can also write it this way.
[latex]\sqrt{3x}=\sqrt{3}\cdot \sqrt{x}[/latex]
Look at that—you can think of any number underneath a radical as the product of separate factors, each underneath its own radical.
A Product Raised to a Power Rule or sometimes called The Square Root of a Product Rule
For any real numbers a and b, [latex]\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
For example: [latex]\sqrt{100}=\sqrt{10}\cdot \sqrt{10}[/latex], and [latex]\sqrt{75}=\sqrt{25}\cdot \sqrt{3}[/latex]
This rule is important because it helps you think of one radical as the product of multiple radicals. If you can identify perfect squares within a radical, as with [latex]\sqrt{(2\cdot 2)(2\cdot 2)(3\cdot 3})[/latex], you can rewrite the expression as the product of multiple perfect squares: [latex]\sqrt{{{2}^{2}}}\cdot \sqrt{{{2}^{2}}}\cdot \sqrt{{{3}^{2}}}[/latex].
The square root of a product rule will help us simplify roots that aren’t perfect, as is shown the following example.
Example
Simplify. [latex]\sqrt{63}[/latex]
The final answer [latex]3\sqrt{7}[/latex] may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”
The following video shows more examples of how to simplify square roots that do not have perfect square radicands.
Before we move on to simplifying more complex radicals with variables, we need to learn about an important behavior of square roots with variables in the radicand.
Consider the expression [latex]\sqrt{{{x}^{2}}}[/latex]. This looks like it should be equal to x, right? Let’s test some values for x and see what happens.
In the chart below, look along each row and determine whether the value of x is the same as the value of [latex]\sqrt{{{x}^{2}}}[/latex]. Where are they equal? Where are they not equal?
After doing that for each row, look again and determine whether the value of [latex]\sqrt{{{x}^{2}}}[/latex] is the same as the value of [latex]\left|x\right|[/latex].
| [latex]x[/latex] | [latex]x^{2}[/latex] | [latex]\sqrt{x^{2}}[/latex] | [latex]\left|x\right|[/latex] |
|---|---|---|---|
| [latex]−5[/latex] | 25 | 5 | 5 |
| [latex]−2[/latex] | 4 | 2 | 2 |
| 0 | 0 | 0 | 0 |
| 6 | 36 | 6 | 6 |
| 10 | 100 | 10 | 10 |
Notice—in cases where x is a negative number, [latex]\sqrt{x^{2}}\neq{x}[/latex]! However, in all cases [latex]\sqrt{x^{2}}=\left|x\right|[/latex]. You need to consider this fact when simplifying radicals with an even index that contain variables, because by definition [latex]\sqrt{x^{2}}[/latex] is always nonnegative.
Taking the Square Root of a Radical Expression
When finding the square root of an expression that contains variables raised to a power, consider that [latex]\sqrt{x^{2}}=\left|x\right|[/latex].
Examples: [latex]\sqrt{9x^{2}}=3\left|x\right|[/latex], and [latex]\sqrt{16{{x}^{2}}{{y}^{2}}}=4\left|xy\right|[/latex]
We will combine this with the square root of a product rule in our next example to simplify an expression with three variables in the radicand.
Example
Simplify. [latex]\sqrt{{{a}^{3}}{{b}^{5}}{{c}^{2}}}[/latex]
Analysis of the Solution
Why didn’t we write [latex]b^2[/latex] as [latex]|b^2|[/latex]? Because when you square a number, you will always get a positive result, so the principal square root of [latex]\left(b^2\right)^2[/latex] will always be non-negative. One tip for knowing when to apply the absolute value after simplifying any even indexed root is to look at the final exponent on your variable terms. If the exponent is odd – including 1 – add an absolute value. This applies to simplifying any root with an even index, as we will see in later examples.
In the following video you will see more examples of how to simplify radical expressions with variables.
We will show another example where the simplified expression contains variables with both odd and even powers.
Example
Simplify. [latex]\sqrt{9{{x}^{6}}{{y}^{4}}}[/latex]
In our next example we will start with an expression written with a rational exponent. You will see that you can use a similar process – factoring and sorting terms into squares – to simplify this expression.
Example
Simplify. [latex]{{(36{{x}^{4}})}^{\frac{1}{2}}}[/latex]
Here is one more example with perfect squares.
Example
Simplify. [latex]\sqrt{49{{x}^{10}}{{y}^{8}}}[/latex]
Simplify cube roots
We can use the same techniques we have used for simplifying square roots to simplify higher order roots. For example to simplify a cube root, the goal is to find factors under the radical that are perfect cubes so that you can take their cube root. We no longer need to be concerned about whether we have identified the principal root since we are now finding cube roots. Focus on finding identical trios of factors as you simplify.
Example
Simplify. [latex]\sqrt[3]{40{{m}^{5}}}[/latex]
Remember that you can take the cube root of a negative expression. In the next example we will simplify a cube root with a negative radicand.
Example
Simplify. [latex]\sqrt[3]{-27{{x}^{4}}{{y}^{3}}}[/latex]
You could check your answer by performing the inverse operation. If you are right, when you cube [latex]-3xy\sqrt[3]{x}[/latex] you should get [latex]-27{{x}^{4}}{{y}^{3}}[/latex].
[latex]\begin{array}{l}\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right)\\-3\cdot -3\cdot -3\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\\-27\cdot {{x}^{3}}\cdot {{y}^{3}}\cdot \sqrt[3]{{{x}^{3}}}\\-27{{x}^{3}}{{y}^{3}}\cdot x\\-27{{x}^{4}}{{y}^{3}}\end{array}[/latex]
You can also skip the step of factoring out the negative one once you are comfortable with identifying cubes.
Example
Simplify. [latex]\sqrt[3]{-24{{a}^{5}}}[/latex]
You can check your answer by squaring it to be sure it equals [latex]100{{x}^{2}}{{y}^{4}}[/latex].
In the following video we show more examples of simlifying cube roots.
Simplifying fourth roots
Now let’s move to simplifying fourth degree roots. No matter what root you are simplifying, the same idea applies, find cubes for cube roots, powers of four for fourth roots, etc. Recall that when your simplified expression contains an even indexed radical and a variable factor with an odd exponent, you need to apply an absolute value.
Example
Simplify. [latex]\sqrt[4]{81{{x}^{8}}{{y}^{3}}}[/latex]
An alternative method to factoring is to rewrite the expression with rational exponents, then use the rules of exponents to simplify. You may find that you prefer one method over the other. Either way, it is nice to have options. We will show the last example again, using this idea.
Example
Simplify. [latex]\sqrt[4]{81{{x}^{8}}{{y}^{3}}}[/latex]
In the following video we show another example of how to simplify a fourth and fifth root.
For our last example, we will simplify a more complicated expression, [latex]\large\frac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3]{8{{b}^{4}}}}[/latex]. This expression has two variables, a fraction, and a radical. Let’s take it step-by-step and see if using fractional exponents can help us simplify it.
We will start by simplifying the denominator, since this is where the radical sign is located. Recall that an exponent in the denominator or a fraction can be rewritten as a negative exponent.
Example
Simplify. [latex]\large\frac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3]{8{{b}^{4}}}}[/latex]
Well, that took a while, but you did it. You applied what you know about fractional exponents, negative exponents, and the rules of exponents to simplify the expression.
In our last video we show how to use rational exponents to simplify radical expressions.
Summary
A radical expression is a mathematical way of representing the nth root of a number. Square roots and cube roots are the most common radicals, but a root can be any number. To simplify radical expressions, look for exponential factors within the radical, and then use the property [latex]\sqrt[n]{{{x}^{n}}}=x[/latex] if n is odd, and [latex]\sqrt[n]{{{x}^{n}}}=\left| x \right|[/latex] if n is even to pull out quantities. All rules of integer operations and exponents apply when simplifying radical expressions.
The steps to consider when simplifying a radical are outlined below.
Simplifying a radical
When working with exponents and radicals:
- If n is odd, [latex]\sqrt[n]{{{x}^{n}}}=x[/latex].
- If n is even, [latex]\sqrt[n]{{{x}^{n}}}=\left| x \right|[/latex]. (The absolute value accounts for the fact that if x is negative and raised to an even power, that number will be positive, as will the nth principal root of that number.)
Summary
The square root of a number is the number which, when multiplied by itself, gives the original number. Principal square roots are always positive and the square root of 0 is 0. You can only take the square root of values that are greater than or equal to 0. The square root of a perfect square will be an integer. Other roots can be simplified by identifying factors that are perfect squares, cubes, etc. Nth roots can be approximated using trial and error or a calculator.
Any radical in the form [latex]\sqrt[n]{a^{x}}[/latex] can be written using a fractional exponent in the form [latex]a^{\frac{x}{n}}[/latex]. Rewriting radicals using fractional exponents can be useful in simplifying some radical expressions. When working with fractional exponents, remember that fractional exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
Candela Citations
- Simplify a Variety of Square Expressions (Simplify Perfectly). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/2cWAkmJoaDQ. License: CC BY: Attribution
- Simplify Cube Roots (Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/9Nh-Ggd2VJo. License: CC BY: Attribution
- Simplify Perfect Nth Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/vA2DkcUSRSk. License: CC BY: Attribution
- Approximate a Square Root to Two Decimal Places Using Trial and Error. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/iNfalyW7olk. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Write Expressions Using Radicals and Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/5cWkVrANBWA. License: CC BY: Attribution
- Simplify Square Roots (Not Perfect Square Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/oRd7aBCsmfU. License: CC BY: Attribution
- Simplify Square Roots with Variables. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/q7LqsKPoAKo. License: CC BY: Attribution
- Simplify Cube Roots (Not Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/BtJruOpmHCE. License: CC BY: Attribution
- Simplify Nth Roots with Variables. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/op2LEb0YRyw. License: CC BY: Attribution
- Simplify Radicals Using Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/CfxhFRHUq_M. License: CC BY: Attribution
- Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Precalculus. Authored by: Abramson, Jay. Provided by: Open Stax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution. License Terms: Download for free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface