Why learn to solve problems involving quadratic functions?
 An arrow is shot into the air. How high will it go? How far away will it land? It turns out that you can answer these and related questions with just a little knowledge of quadratic functions. In fact quadratic functions can be used to track to the position of any object that has been thrown, shot, or launched near the surface of the Earth. As long as wind resistance does not play a huge role and the distances are not too great, you can use a quadratic function to model the flight path.
An arrow is shot into the air. How high will it go? How far away will it land? It turns out that you can answer these and related questions with just a little knowledge of quadratic functions. In fact quadratic functions can be used to track to the position of any object that has been thrown, shot, or launched near the surface of the Earth. As long as wind resistance does not play a huge role and the distances are not too great, you can use a quadratic function to model the flight path.
For example, suppose an archer fires an arrow from a height of 2 meters above sea level on a calm day. While the arrow is in the air, someone else tracks and records its height precisely at each second. The following table shows the arrow’s height (meters) versus time (seconds).
| Time ([latex]t[/latex]) | Height ([latex]h[/latex]) |
| 0 sec. | 2 m |
| 1 sec. | 16.7m |
| 2 sec. | 21.6 m |
Let’s plot the data on a coordinate plane.
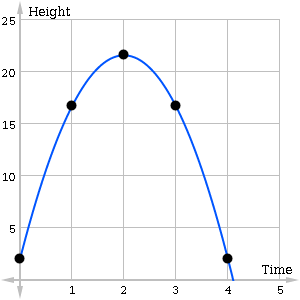
Notice the up-and-down shape? As Isaac Newton would say, what goes up must come down. The smooth arc, first rising and then falling, is a tell-tale clue that there is a quadratic function lurking in the data. The curve that best fits this situation is a parabola, which is what we call the graph of a quadratic function. With a little more work, you can find the equation of this function:
[latex]h(t)=-4.9t^2+19.6t+2[/latex]
In the above equation [latex]t[/latex] represents time in seconds, and [latex]h[/latex] represents height in meters. This is an example of a quadratic function. By analyzing the function you can figure out precisely how high the arrow will go and when it will hit the ground.
In this module you’ll learn how to graph and analyze quadratic functions and discover many other useful applications in which they play a role.
Candela Citations
- Why It Matters: Quadratic Functions. Authored by: Lumen Learning. License: CC BY: Attribution
- Graph of parabolic motion. Authored by: Lumen Learning. License: CC BY: Attribution
- Woman Holding Bow and Arrow. Located at: http://maxpixel.freegreatpicture.com/Archery-Arch-Bow-And-Arrow-Objectives-Woman-782503. License: Public Domain: No Known Copyright