Learning Outcomes
- Use summation notation.
- Use the formula for the sum of the first n terms of a series.
Using Summation Notation
To find the total amount of money in the college fund and the sum of the amounts deposited, we need to add the amounts deposited each month and the amounts earned monthly. The sum of the terms of a sequence is called a series. Consider, for example, the following series.
[latex]3+7+11+15+19+\cdots[/latex]
The [latex]n\text{th }[/latex] partial sum of a series is the sum of a finite number of consecutive terms beginning with the first term. The notation
[latex]\begin{align}&{S}_{n}\text{ represents the partial sum.} \\ &{S}_{1}=3 \\ &{S}_{2}=3+7=10 \\ &{S}_{3}=3+7+11=21 \\ &{S}_{4}=3+7+11+15=36\end{align}[/latex]
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, [latex]\Sigma[/latex], to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series.
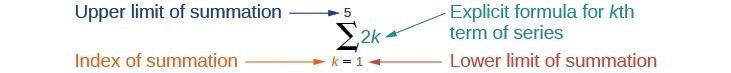
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.
[latex]\begin{align} &{a}_{1}=2\left(1\right)=2 \\ &{a}_{2}=2\left(2\right)=4 \\ &{a}_{3}=2\left(3\right)=6 \\ &{a}_{4}=2\left(4\right)=8 \\ &{a}_{5}=2\left(5\right)=10 \end{align}[/latex]
We can find the sum of the series by adding the terms:
[latex]\sum\limits _{k=1}^{5}2k=2+4+6+8+10=30[/latex]
A General Note: Summation Notation
The sum of the first [latex]n[/latex] terms of a series can be expressed in summation notation as follows:
[latex]\sum\limits _{k=1}^{n}{a}_{k}[/latex]
This notation tells us to find the sum of [latex]{a}_{k}[/latex] from
[latex]k=1[/latex] to [latex]k=n[/latex].
[latex]k[/latex] is called the index of summation, 1 is the lower limit of summation, and [latex]n[/latex] is the upper limit of summation.
Q & A
Does the lower limit of summation have to be 1?
No. The lower limit of summation can be any number, but 1 is frequently used. We will look at examples with lower limits of summation other than 1.
How To: Given summation notation for a series, evaluate the value.
- Identify the lower limit of summation.
- Identify the upper limit of summation.
- Substitute each value of [latex]k[/latex] from the lower limit to the upper limit into the formula.
- Add to find the sum.
Example: Using Summation Notation
Evaluate [latex]\sum\limits _{k=3}^{7}{k}^{2}[/latex].
Try It
Evaluate [latex]\sum\limits _{k=2}^{5}\left(3k - 1\right)[/latex].
Key Concepts
- The sum of the terms in a sequence is called a series.
- A common notation for series is called summation notation, which uses the Greek letter sigma to represent the sum.
Glossary
index of summation in summation notation, the variable used in the explicit formula for the terms of a series and written below the sigma with the lower limit of summation
lower limit of summation the number used in the explicit formula to find the first term in a series
summation notation a notation for series using the Greek letter sigma; it includes an explicit formula and specifies the first and last terms in the series
upper limit of summation the number used in the explicit formula to find the last term in a series
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 5865, 5867. Authored by: WebWork-Rochester. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY +GPL
- Question ID 128790,128791. Authored by: Day, Alyson. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 20277. Authored by: Kissel, Kris. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 23741. Authored by: Shahbazian, Roy, mb McClure, Caren. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution