Inverse Trigonometric Functions
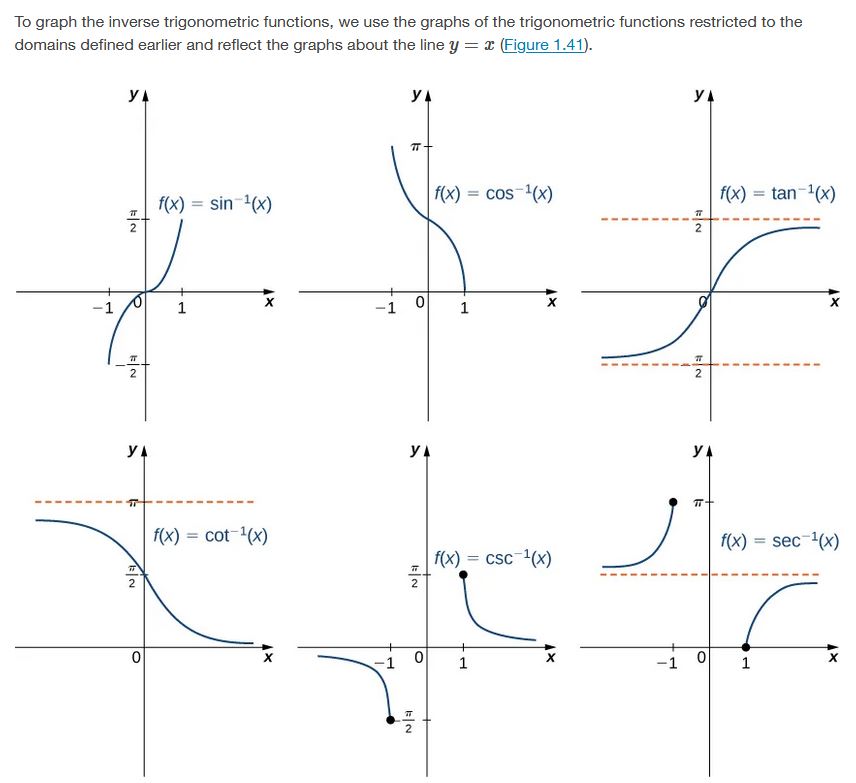
The six basic trigonometric functions are periodic, and therefore they are not one-to-one. However, if we restrict the domain of a trigonometric function to an interval where it is one-to-one, we can define its inverse. Consider the sine function (Figure 1.34). The sine function is one-to-one on an infinite number of intervals, but the standard convention is to restrict the domain to the interval [−π/2,π/2]. By doing so, we define the inverse sine function on the domain [−1,1] such that for any x in the interval [−1,1], the inverse sine function tells us which angle θ in the interval [−π/2,π/2] satisfies sinθ=x. Similarly, we can restrict the domains of the other trigonometric functions to define inverse trigonometric functions, which are functions that tell us which angle in a certain interval has a specified trigonometric value.

Exercises
\
Try It
Try It
Examples
Try It
Examples
