1. For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.

2. When a right triangle with a hypotenuse of 1 is placed in the unit circle, which sides of the triangle correspond to the x– and y-coordinates?

3. The tangent of an angle compares which sides of the right triangle?

4. What is the relationship between the two acute angles in a right triangle?

5. Explain the cofunction identity.

For the following exercises, use cofunctions of complementary angles.

6. [latex]\cos \left(34^\circ\right)=\sin \left(\text{__}^\circ\right)[/latex]

7. [latex]\cos \left(\frac{\pi }{3}\right)=\sin \text{(___)}[/latex]

8. [latex]\csc \left(21^\circ\right)=\sec \left(\text{___}^\circ \right)[/latex]

9. [latex]\tan \left(\frac{\pi }{4}\right)=\cot \left(\text{__}\right)[/latex]

For the following exercises, find the lengths of the missing sides if side [latex]a[/latex] is opposite angle [latex]A[/latex], side [latex]b[/latex] is opposite angle [latex]B[/latex], and side [latex]c[/latex] is the hypotenuse.

10. [latex]\cos B=\frac{4}{5},a=10[/latex]

11. [latex]\sin B=\frac{1}{2}, a=20[/latex]

12. [latex]\tan A=\frac{5}{12},b=6[/latex]

13. [latex]\tan A=100,b=100[/latex]

14. [latex]\sin B=\frac{1}{\sqrt{3}}, a=2[/latex]

15. [latex]a=5,\measuredangle A={60}^{\circ }[/latex]

16. [latex]c=12,\measuredangle A={45}^{\circ }[/latex]

For the following exercises, use Figure 14 to evaluate each trigonometric function of angle [latex]A[/latex].

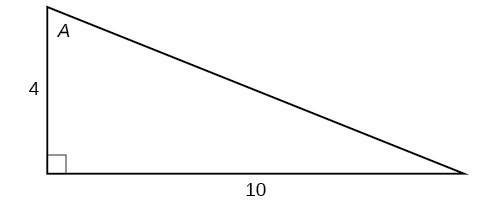
Figure 14

17. [latex]\sin A[/latex]

18. [latex]\cos A[/latex]

19. [latex]\tan A[/latex]

20. [latex]\csc A[/latex]

21. [latex]\sec A[/latex]

22. [latex]\cot A[/latex]

For the following exercises, use Figure 15 to evaluate each trigonometric function of angle [latex]A[/latex].

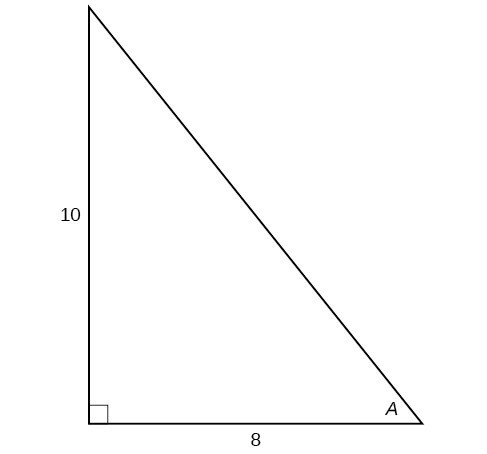
Figure 15

23. [latex]\sin A[/latex]

24. [latex]\cos A[/latex]

25. [latex]\tan A[/latex]

26. [latex]\csc A[/latex]

27. [latex]\sec A[/latex]

28. [latex]\cot A[/latex]

For the following exercises, solve for the unknown sides of the given triangle.

29.

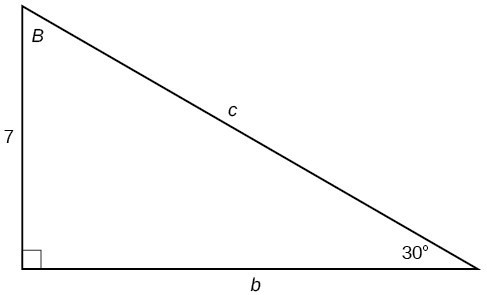
30.

31.

For the following exercises, use a calculator to find the length of each side to four decimal places.

32.

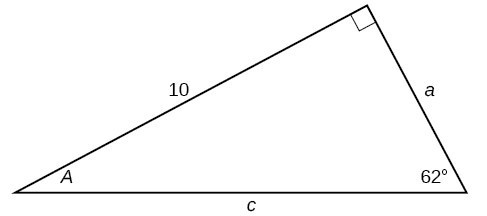
33.

34.

35.

36.

37. [latex]b=15,\measuredangle B={15}^{\circ }[/latex]

38. [latex]c=200,\measuredangle B={5}^{\circ }[/latex]

39. [latex]c=50,\measuredangle B={21}^{\circ }[/latex]

40. [latex]a=30,\measuredangle A={27}^{\circ }[/latex]

41. [latex]b=3.5,\measuredangle A={78}^{\circ }[/latex]

42. Find [latex]x[/latex].

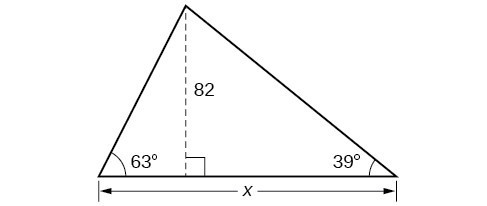
43. Find [latex]x[/latex].

44. Find [latex]x[/latex].

45. Find [latex]x[/latex].

46. A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]36^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]23^\circ [/latex]. How tall is the tower?

47. A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]43^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]31^\circ [/latex]. How tall is the tower?

48. A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]15^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]2^\circ [/latex]. How far is the person from the monument?

49. A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]18^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]3^\circ [/latex]. How far is the person from the monument?

50. There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]40^\circ [/latex]. From the same location, the angle of elevation to the top of the antenna is measured to be [latex]43^\circ [/latex]. Find the height of the antenna.

51. There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]36^\circ [/latex]. From the same location, the angle of elevation to the top of the lightning rod is measured to be [latex]38^\circ [/latex]. Find the height of the lightning rod.

52. A 33-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ [/latex]. How high does the ladder reach up the side of the building?

53. A 23-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ [/latex]. How high does the ladder reach up the side of the building?

54. The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.

55. The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.

56. Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be [latex]60^\circ [/latex], how far from the base of the tree am I?