1. Explain the difference between a value at [latex]x=a[/latex] and the limit as [latex]x[/latex] approaches [latex]a[/latex].
2. Explain why we say a function does not have a limit as [latex]x[/latex] approaches [latex]a[/latex] if, as [latex]x[/latex] approaches [latex]a[/latex], the left-hand limit is not equal to the right-hand limit.
For the following exercises, estimate the functional values and the limits from the graph of the function [latex]f[/latex] provided in Figure 14.
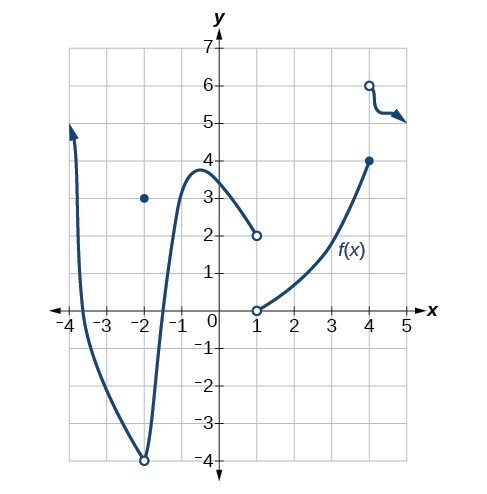
Figure 14
3. [latex]\underset{x\to -{2}^{-}}{\mathrm{lim}}f\left(x\right)[/latex]
4. [latex]\underset{x\to -{2}^{+}}{\mathrm{lim}}f\left(x\right)[/latex]
5. [latex]\underset{x\to -2}{\mathrm{lim}}f\left(x\right)[/latex]
6. [latex]f\left(-2\right)[/latex]
7. [latex]\underset{x\to -{1}^{-}}{\mathrm{lim}}f\left(x\right)[/latex]
8. [latex]\underset{x\to {1}^{+}}{\mathrm{lim}}f\left(x\right)[/latex]
9. [latex]\underset{x\to 1}{\mathrm{lim}}f\left(x\right)[/latex]
10. [latex]f\left(1\right)[/latex]
11. [latex]\underset{x\to {4}^{-}}{\mathrm{lim}}f\left(x\right)[/latex]
12. [latex]\underset{x\to {4}^{+}}{\mathrm{lim}}f\left(x\right)[/latex]
13. [latex]\underset{x\to 4}{\mathrm{lim}}f\left(x\right)[/latex]
14. [latex]f\left(4\right)[/latex]
For the following exercises, draw the graph of a function from the functional values and limits provided.
15. [latex]\underset{x\to {0}^{-}}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {0}^{+}}{\mathrm{lim}}f\left(x\right)=-3,\underset{x\to 2}{\mathrm{lim}}f\left(x\right)=2,f\left(0\right)=4,f\left(2\right)=-1,f\left(-3\right)\text{ does not exist}[/latex].
16. [latex]\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=0,\underset{x\to {2}^{+}}{\mathrm{lim}}=-2,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=3,f\left(2\right)=5,f\left(0\right)[/latex]
17. [latex]\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)=-3,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=5,f\left(0\right)=1,f\left(1\right)=0[/latex]
18. [latex]\underset{x\to {3}^{-}}{\mathrm{lim}}f\left(x\right)=0,\underset{x\to {3}^{+}}{\mathrm{lim}}f\left(x\right)=5,\underset{x\to 5}{\mathrm{lim}}f\left(x\right)=0,f\left(5\right)=4,f\left(3\right)\text{ does not exist}[/latex].
19. [latex]\underset{x\to 4}{\mathrm{lim}}f\left(x\right)=6,\underset{x\to {6}^{+}}{\mathrm{lim}}f\left(x\right)=-1,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=5,f\left(4\right)=6,f\left(2\right)=6[/latex]
20. [latex]\underset{x\to -3}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {1}^{+}}{\mathrm{lim}}f\left(x\right)=-2,\underset{x\to 3}{\mathrm{lim}}f\left(x\right)=-4,f\left(-3\right)=0,f\left(0\right)=0[/latex]
21. [latex]\underset{x\to \pi }{\mathrm{lim}}f\left(x\right)={\pi }^{2},\underset{x\to -\pi }{\mathrm{lim}}f\left(x\right)=\frac{\pi }{2},\underset{x\to {1}^{-}}{\mathrm{lim}}f\left(x\right)=0,f\left(\pi \right)=\sqrt{2},f\left(0\right)\text{ does not exist}[/latex].
For the following exercises, use a graphing calculator to determine the limit to 5 decimal places as [latex]x[/latex] approaches 0.
22. [latex]f\left(x\right)={\left(1+x\right)}^{\frac{1}{x}}[/latex]
23. [latex]g\left(x\right)={\left(1+x\right)}^{\frac{2}{x}}[/latex]
24. [latex]h\left(x\right)={\left(1+x\right)}^{\frac{3}{x}}[/latex]
25. [latex]i\left(x\right)={\left(1+x\right)}^{\frac{4}{x}}[/latex]
26. [latex]j\left(x\right)={\left(1+x\right)}^{\frac{5}{x}}[/latex]
27. Based on the pattern you observed in the exercises above, make a conjecture as to the limit of [latex]f\left(x\right)={\left(1+x\right)}^{\frac{6}{x}}[/latex], [latex]g\left(x\right)={\left(1+x\right)}^{\frac{7}{x}}[/latex], [latex]\text{and }h\left(x\right)={\left(1+x\right)}^{\frac{n}{x}}[/latex].
For the following exercises, use a graphing utility to find graphical evidence to determine the left- and right-hand limits of the function given as [latex]x[/latex] approaches [latex]a[/latex]. If the function has a limit as [latex]x[/latex] approaches [latex]a[/latex], state it. If not, discuss why there is no limit.
28. [latex]f\left(x\right)=\begin{cases}|x|-1,\hfill& \text{if }x\ne 1 \\ x^{3}, \hfill& \text{if }x=1\end{cases};\text{ }a=1[/latex]
29. [latex]f\left(x\right)=\begin{cases}\dfrac{1}{x+1},\hfill& \text{if }x=−2 \\ \left(x+1\right)^{2},\hfill& \text{if }x\ne−2\end{cases};\text{ }a=−2[/latex]
For the following exercises, use numerical evidence to determine whether the limit exists at [latex]x=a[/latex]. If not, describe the behavior of the graph of the function near [latex]x=a[/latex]. Round answers to two decimal places.
30. [latex]f\left(x\right)=\frac{{x}^{2}-4x}{16-{x}^{2}};a=4[/latex]
31. [latex]f\left(x\right)=\frac{{x}^{2}-x - 6}{{x}^{2}-9};a=3[/latex]
32. [latex]f\left(x\right)=\frac{{x}^{2}-6x - 7}{{x}^{2}- 7x};a=7[/latex]
33. [latex]f\left(x\right)=\frac{{x}^{2}-1}{{x}^{2}-3x+2};a=1[/latex]
34. [latex]f\left(x\right)=\frac{1-{x}^{2}}{{x}^{2}-3x+2};a=1[/latex]
35. [latex]f\left(x\right)=\frac{10 - 10{x}^{2}}{{x}^{2}-3x+2};a=1[/latex]
36. [latex]f\left(x\right)=\frac{x}{6{x}^{2}-5x - 6};a=\frac{3}{2}[/latex]
37. [latex]f\left(x\right)=\frac{x}{4{x}^{2}+4x+1};a=-\frac{1}{2}[/latex]
38. [latex]f\left(x\right)=\frac{2}{x - 4};\text{ }a=4[/latex]
For the following exercises, use a calculator to estimate the limit by preparing a table of values. If there is no limit, describe the behavior of the function as [latex]x[/latex] approaches the given value.
39. [latex]\underset{x\to 0}{\mathrm{lim}}\dfrac{7\tan x}{3x}[/latex]
40. [latex]\underset{x\to 4}{\mathrm{lim}}\dfrac{{x}^{2}}{x - 4}[/latex]
41. [latex]\underset{x\to 0}{\mathrm{lim}}\dfrac{2\sin x}{4\tan x}[/latex]
For the following exercises, use a graphing utility to find numerical or graphical evidence to determine the left and right-hand limits of the function given as [latex]x[/latex] approaches [latex]a[/latex]. If the function has a limit as [latex]x[/latex] approaches [latex]a[/latex], state it. If not, discuss why there is no limit.
42. [latex]\underset{x\to 0}{\mathrm{lim}}{e}^{{e}^{\frac{1}{x}}}[/latex]
43. [latex]\underset{x\to 0}{\mathrm{lim}}{e}^{{e}^{-\frac{1}{{x}^{2}}}}[/latex]
44. [latex]\underset{x\to 0}{\mathrm{lim}}\dfrac{|x|}{x}[/latex]
45. [latex]\underset{x\to -1}{\mathrm{lim}}\dfrac{|x+1|}{x+1}[/latex]
46. [latex]\underset{x\to 5}{\mathrm{lim}}\dfrac{|x - 5|}{5-x}[/latex]
47. [latex]\underset{x\to -1}{\mathrm{lim}}\dfrac{1}{{\left(x+1\right)}^{2}}[/latex]
48. [latex]\underset{x\to 1}{\mathrm{lim}}\dfrac{1}{{\left(x - 1\right)}^{3}}[/latex]
49. [latex]\underset{x\to 0}{\mathrm{lim}}\dfrac{5}{1-{e}^{\frac{2}{x}}}[/latex]
50. Use numerical and graphical evidence to compare and contrast the limits of two functions whose formulas appear similar: [latex]f\left(x\right)=\left\rvert\frac{1-x}{x}\right\rvert[/latex] and [latex]g\left(x\right)=\left\rvert\frac{1+x}{x}\right\rvert[/latex] as [latex]x[/latex] approaches 0. Use a graphing utility, if possible, to determine the left- and right-hand limits of the functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] as [latex]x[/latex] approaches 0. If the functions have a limit as [latex]x[/latex] approaches 0, state it. If not, discuss why there is no limit.
51. According to the Theory of Relativity, the mass [latex]m[/latex] of a particle depends on its velocity [latex]v[/latex] . That is
[latex]m=\frac{{m}_{o}}{\sqrt{1-\left({v}^{2}/{c}^{2}\right)}}[/latex]
where [latex]{m}_{o}[/latex] is the mass when the particle is at rest and [latex]c[/latex] is the speed of light. Find the limit of the mass, [latex]m[/latex], as [latex]v[/latex] approaches [latex]{c}^{-}[/latex].
52. Allow the speed of light, [latex]c[/latex], to be equal to 1.0. If the mass, [latex]m[/latex], is 1, what occurs to [latex]m[/latex] as [latex]v\to c?[/latex] Using the values listed in the table below, make a conjecture as to what the mass is as [latex]v[/latex] approaches 1.00.
| [latex]v[/latex] | [latex]m[/latex] |
| 0.5 | 1.15 |
| 0.9 | 2.29 |
| 0.95 | 3.20 |
| 0.99 | 7.09 |
| 0.999 | 22.36 |
| 0.99999 | 223.61 |
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution. License Terms: Download for free at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface
