Properties of Light
Learning Objectives
- Describe problems with Rutherford’s model of the atom.
- List types of electromagnetic radiation
What are waves?
 Waves can come in many sizes. Here we see a large wave crashing on the beach. Other waves can be very small and regular. We normally think of waves as being made of water, but there are forms of energy that take on the characteristics of waves.
Waves can come in many sizes. Here we see a large wave crashing on the beach. Other waves can be very small and regular. We normally think of waves as being made of water, but there are forms of energy that take on the characteristics of waves.
The idea of a wave has played a major role in our understanding of how the atom is put together and why it behaves the way it does.
The nuclear atomic model proposed by Rutherford was a great improvement over previous models, but was still not complete. It did not fully explain the location and behavior of the electrons in the vast space outside of the nucleus. In fact, it was well known that oppositely charged particles attract one another. Rutherford’s model did not explain why the electrons don’t simply move toward and eventually collide with the nucleus. Experiments in the early twentieth century began to focus on the absorption and emission of light by matter. These studies showed how certain phenomena associated with light reveal insight into the nature of matter, energy, and atomic structure.
Wave Nature of Light
In order to begin to understand the nature of the electron, we first need to look at the properties of light. Prior to 1900, scientists thought light behaved solely as a wave. As we will see later, this began to change as new experiments demonstrated that light also has some of the characteristics of a particle. First, we will examine the wavelike properties of light.
Visible light is one type of electromagnetic radiation, which is a form of energy that exhibits wavelike behavior as it moves through space. Other types of electromagnetic radiation include gamma rays, x-rays, ultraviolet light, infrared light, microwaves, and radio waves. The figure below shows the electromagnetic spectrum , which is all forms of electromagnetic radiation. Notice that visible light makes up only a very, very small portion of the entire electromagnetic spectrum. All electromagnetic radiation moves through a vacuum at a constant speed of 2.998 × 10 8 m/s. While the presence of air molecules slows the speed of light by a very small amount, we will use the value of 3.00 × 10 8 m/s as the speed of light in air.
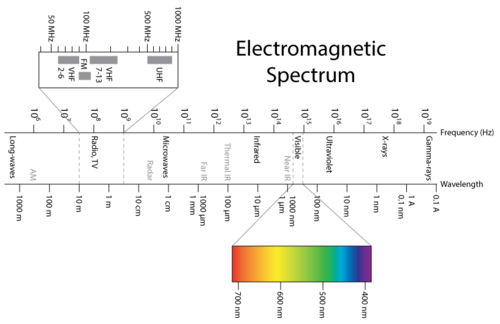
Figure 1. The electromagnetic spectrum encompasses a very wide range of wavelengths and frequencies. Visible light is only a very small portion of the spectrum with wavelengths from 400-700 nm.
Figure 1 shows how the electromagnetic spectrum displays a wide variation in wavelength and frequency. Radio waves have wavelengths of as long as hundreds of meters, while the wavelength of gamma rays are on the order of 10−12 m. The corresponding frequencies range from 106 to 1021 Hz. Visible light can be split into colors with the use of a prism (Figure 2), yielding the visible spectrum of light. Red light has the longest wavelength and lowest frequency, while violet light has the shortest wavelength and highest frequency. Visible light wavelength ranges from about 400–700 nm with frequencies in the range of 10 14 Hz.
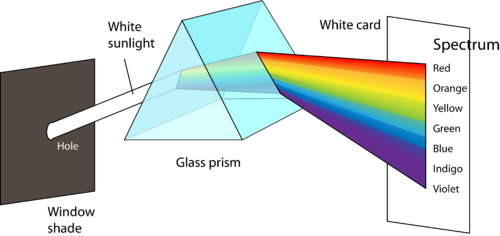
Figure 2. A small beam of white light is (refracted) bent as it passes through a glass prism. The shorter the wavelength of light, the greater is the refraction, so the light is separated into all its colors.
Summary
- Electromagnetic radiation is a form of energy.
- Visible light has wavelengths from 400–700 nm.
- The speed of light in air is 3.00 × 108 m/s.
Practice
Read this page on Measuring the Speed of Light to answer the following questions:
- Who first tried to measure the speed of light?
- How long would it take for light to travel the one mile distance that Galileo studied?
- What astronomical object did Ole Roemer use to determine the speed of light?
- What did Roemer determine the speed of light to be?
Review
- What did Rutherford’s nuclear atomic model not explain?
- Prior to 1900, what did scientists believe about the nature of light?
- What is visible light?
- What is the range of wavelengths for visible light?
Glossary
- electromagnetic radiation: A form of energy that exhibits wavelike behavior as it moves through space.
- electromagnetic spectrum: All forms of electromagnetic radiation.
Wavelength and Frequency Calculations
Learning Objectives
- Define wavelength.
- Define frequency.
- Describe the characteristics of a wave.
- Perform calculations involving wavelength and frequency.
Do you enjoy going to the beach?

During the summer, almost everyone enjoys going to the beach. They can swim, have picnics, and work on their tans. But if you get too much sun, you can burn. A particular set of solar wavelengths are especially harmful to the skin. This portion of the soar spectrum is known as UV B, with wavelengths of 280-320 nm. Sunscreens are effective in protecting the skin against both the immediate skin damage and the long-term possibility of skin cancer.
Waves
Waves are characterized by their repetitive motion. Imagine a toy boat riding the waves in a wave pool. As the water wave passes under the boat, it moves up and down in a regular and repeated fashion. While the wave travels horizontally, the boat only travels vertically up and down. Figure 3 shows two examples of waves.
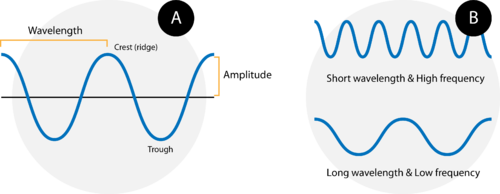
Figure 3. (A) A wave consists of alternation crests and troughs. The wavelength (λ) is defined as the distance between any two consecutive identical points on the waveform. The amplitude is the height of the wave. (B) A wave with a short wavelength (top) has a high frequency because more waves pass a given point in a certain amount of time. A wave with a longer wavelength (bottom) has a lower frequency.
A wave cycle consists of one complete wave – starting at the zero point, going up to a wave crest , going back down to a wave trough , and back to the zero point again. The wavelength of a wave is the distance between any two corresponding points on adjacent waves. It is easiest to visualize the wavelength of a wave as the distance from one wave crest to the next. In an equation, wavelength is represented by the Greek letter lambda ![]() . Depending on the type of wave, wavelength can be measured in meters, centimeters, or nanometers (1 m = 10 9 nm). The frequency , represented by the Greek letter nu
. Depending on the type of wave, wavelength can be measured in meters, centimeters, or nanometers (1 m = 10 9 nm). The frequency , represented by the Greek letter nu ![]() , is the number of waves that pass a certain point in a specified amount of time. Typically, frequency is measured in units of cycles per second or waves per second. One wave per second is also called a Hertz (Hz) and in SI units is a reciprocal second (s -1 ).
, is the number of waves that pass a certain point in a specified amount of time. Typically, frequency is measured in units of cycles per second or waves per second. One wave per second is also called a Hertz (Hz) and in SI units is a reciprocal second (s -1 ).
Figure B above shows an important relationship between the wavelength and frequency of a wave. The top wave clearly has a shorter wavelength than the second wave. However, if you picture yourself at a stationary point watching these waves pass by, more waves of the first kind would pass by in a given amount of time. Thus the frequency of the first waves is greater than that of the second waves. Wavelength and frequency are therefore inversely related. As the wavelength of a wave increases, its frequency decreases. The equation that relates the two is:
![]()
The variable ![]() is the speed of light. For the relationship to hold mathematically, if the speed of light is used in m/s, the wavelength must be in meters and the frequency in Hertz.
is the speed of light. For the relationship to hold mathematically, if the speed of light is used in m/s, the wavelength must be in meters and the frequency in Hertz.
Sample Problem: Wavelength and Frequency
The color orange within the visible light spectrum has a wavelength of about 620 nm. What is the frequency of orange light?
Step 1: List the known quantities and plan the problem.
Known
- wavelength
 = 620 nm
= 620 nm - speed of light
 = 3.00 × 10 8 m/s
= 3.00 × 10 8 m/s - conversion factor 1 m = 10 9 nm
Unknown
- Frequency
Convert the wavelength to m, then apply the equation ![]() and solve for frequency. Dividing both sides of the equation by
and solve for frequency. Dividing both sides of the equation by ![]() yields:
yields:
![]()
Step 2: Calculate

Step 3: Think about your result.
The value for the frequency falls within the range for visible light.
Summary
- All waves can be defined in terms of their frequency and intensity.
 expresses the relationship between wavelength and frequency.
expresses the relationship between wavelength and frequency.
Practice
Read the material on the link below and answer the questions as they come up:
https://www.absorblearning.com/physics/demo/units/DJFPh064.html
Review
- Define wavelength.
- Define frequency.
- What is the relationship between wavelength and frequency?
Glossary
- amplitude: The height of the wave, the distance between the crest and the trough
- crest: The peak of the wave
- frequency: Is the number of waves that pass a certain point in a specified amount of time.
- trough: The low point of the wave cycle.
- wavelength: The distance between two successive peaks.
Quantization of Energy
Learning Objectives
- Define quantum.
- Describe the relationship between the amount of energy absorbed or released by an object and the frequency of the radiation observed.
Every so often you hear a commercial or a news story with the words “quantum leap” in it. The quantum leap is supposed to be a major breakthrough, a big change, something extraordinarily large. The reality is far different. Instead of the big, extravagant change the “quantum” that scientists know about is a very small difference in the location of an electron around a nucleus – hardly an enormous shift at all.

Figure 4. A heated object may glow different colors. The atoms in this piece of metal are releasing energy in discrete units called quanta.
German physicist Max Planck (1858–1947) studied the emission of light by hot objects. You have likely seen a heated metal object glow an orange-red color (see Figure 4).
Classical physics, which explains the behavior of large, everyday objects, predicted that a hot object would emit electromagnetic energy in a continuous fashion. In other words, every wavelength of light could possibly be emitted. Instead, what Planck found by analyzing the spectra was that the energy of the hot body could only be lost in small discrete units. A quantum is the minimum quantity of energy that can either be lost or gained by an atom. An analogy is that a brick wall can only undergo a change in height by units of one or more bricks and not by any possible height. Planck showed that the amount of radiant energy absorbed or emitted by an object is directly proportional to the frequency of the radiation.
![]()
In the equation, ![]() is the energy, in joules, of a quantum of radiation,
is the energy, in joules, of a quantum of radiation, ![]() is the frequency, and
is the frequency, and ![]() is a fundamental constant called Planck’s constant . The value of Planck’s constant is
is a fundamental constant called Planck’s constant . The value of Planck’s constant is ![]() . The energy of any system must increase or decrease in units of
. The energy of any system must increase or decrease in units of ![]() . A small energy change results in the emission or absorption of low-frequency radiation, while a large energy change results in the emission or absorption of high-frequency radiation.
. A small energy change results in the emission or absorption of low-frequency radiation, while a large energy change results in the emission or absorption of high-frequency radiation.
Sample Problem: Quantized Energy
What is the energy of a photon of green light with a frequency of 5.75 × 10 14 Hz?
Step 1: List the known quantities and plan the problem.
Known
- frequency
 = 5.75 × 10 14 Hz
= 5.75 × 10 14 Hz - Planck’s constant
 = 6.626 × 10 -34 J • s
= 6.626 × 10 -34 J • s
Unknown
- energy

Apply the equation ![]() to solve for the energy.
to solve for the energy.
Step 2: Calculate
![]()
Step 3: Think about your result.
While the resulting energy may seem very small, this is for only one photon of light. Visible quantities of light consist of huge quantities of photons. Recall that a hertz is equal to a reciprocal second, so the units agree in the equation.
Summary
- A quantum relates to the energy gained or absorbed by an object.
- The value of Planck’s constant is
 .
.
Practice
Use the link below to answer the following questions:
http://abyss.uoregon.edu/~js/21st_century_science/lectures/lec12.html
- According to classical physics, what should happen as the electron accelerates around the nucleus?
- What did Planck assume?
- How are changes in energy carried out at the sub-atomic level?
Review
- What did classical physics predict about hot objects?
- What did Planck find?
- What is a quantum?
Glossary
- Planck’s constant:
 .
. - quantum: The minimum quantity of energy that can either be lost or gained by an atom.
Photoelectric Effect
Learning Objectives
Describe the photoelectric effect.
Are you a fan of science fiction?

In old science fiction stories (1950s), one of the space travel themes was the use of solar sails for propulsion. The idea was that the photon pressure from the sun would push the sail (like the wind sails) and move the space craft. What once was science fiction is now reality as solar sails are being developed and tested for modern space travel.
Photoelectric Effect and the Particle Nature of Light
In 1905 Albert Einstein (1879–1955) proposed that light be described as quanta of energy that behave as particles. A photon is a particle of electromagnetic radiation that has zero mass and carries a quantum of energy. The energy of photons of light is quantized according to the ![]() equation. For many years light had been described using only wave concepts, and scientists trained in classical physics found this wave-particle duality of light to be a difficult idea to accept. A key experiment that was explained by Einstein using light’s particle nature was called the photoelectric effect.
equation. For many years light had been described using only wave concepts, and scientists trained in classical physics found this wave-particle duality of light to be a difficult idea to accept. A key experiment that was explained by Einstein using light’s particle nature was called the photoelectric effect.
The photoelectric effect is a phenomenon that occurs when light shined onto a metal surface causes the ejection of electrons from that metal. It was observed that only certain frequencies of light are able to cause the ejection of electrons. If the frequency of the incident light is too low (red light, for example), then no electrons were ejected even if the intensity of the light was very high or it was shone onto the surface for a long time. If the frequency of the light was higher (green light, for example), then electrons were able to be ejected from the metal surface even if the intensity of the light was very low or it was shone for only a short time. This minimum frequency needed to cause electron ejection is referred to as the threshold frequency.
Classical physics was unable to explain the photoelectric effect. If classical physics applied to this situation, the electron in the metal could eventually collect enough energy to be ejected from the surface even if the incoming light was of low frequency. Einstein used the particle theory of light to explain the photoelectric effect as shown in Figure 5.
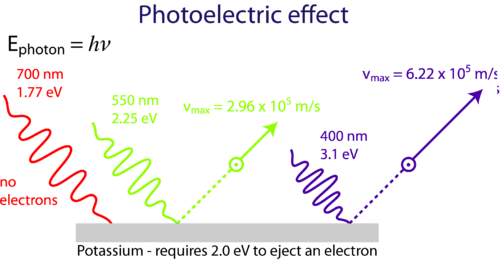
Figure 5. Low frequency light (red) is unable to cause ejection of electrons from the metal surface. At or above the threshold frequency (green) electrons are ejected. Even higher frequency incoming light (blue) causes ejection of the same number of electrons but with greater speed.

Figure 6. Photoelectric cells convert light energy into electrical energy which powers this calculator.
Consider the E = hv equation. The E is the minimum energy that is required in order for the metal’s electron to be ejected.
- If the incoming light’s frequency, v, is below the threshold frequency, there will never be enough energy to cause electron to be ejected.
- If the frequency is equal to or higher than the threshold frequency, electrons will be ejected.
As the frequency increases beyond the threshold, the ejected electrons simply move faster. An increase in the intensity of incoming light that is above the threshold frequency causes the number of electrons that are ejected to increase, but they do not travel any faster.
The photoelectric effect is applied in devices called photoelectric cells, which are commonly found in everyday items such as a calculator which uses the energy of light to generate electricity.
Summary
- Light has properties of both a wave and a particle.
- The photoelectric effect is produced by light striking a metal and dislodging electrons form the surface of the metal.
Practice
Use the link below to answer the following questions:
http://www.citycollegiate.com/physicsXII_photocell.htm
- What is the emitting material in this photocell?
- What causes photoelectrons to be emitted?
- Does the current increase or decrease with an increase in light intensity?
- What happens if light does not strike the cathode?
Review
- What are the properties of a photon?
- What does the photoelectric effect show about the properties of light?
- How does the frequency of light affect the release of photons?
Glossary
- photoelectric cell: Use energy of light to generate electricity.
- photoelectric effect: A phenomenon that occurs when light shined onto a metal surface causes the ejection of electrons from that metal.
- photon: A particle of electromagnetic radiation that has zero mass and carries a quantum of energy.
- threshold frequency: Minimum frequency needed to cause electron ejection.
Atomic Emission Spectra
Learning Objectives
- Define ground state.
- Define excited state.
- Describe how atomic emission spectra are produced.
How much energy does it take to shoot an arrow?

Archery as a sport or a means of defense has existed for centuries. At rest, there is no tension on the bowstring and no force on the arrow. When the string and arrow are pulled back, we now have a situation where kinetic energy (pulling of the string) has been converted to potential energy (the tension on the string). The archer releases the arrow and the potential energy is translated into kinetic energy as the arrow moves. It turns out that electrons behave the same way when energy is put into the system or released from the system.
The electrons in an atom tend to be arranged in such a way that the energy of the atom is as low as possible. The ground state of an atom is the lowest energy state of the atom. When those atoms are given energy, the electrons absorb the energy and move to a higher energy level. These energy levels of the electrons in atoms are quantized, meaning again that the electron must move from one energy level to another in discrete steps rather than continuously. An excited state of an atom is a state where its potential energy is higher than the ground state. An atom in the excited state is not stable. When it returns back to the ground state, it releases the energy that it had previously gained in the form of electromagnetic radiation.
So how do atoms gain energy in the first place? One way is to pass an electric current through an enclosed sample of a gas at low pressure. Since the electron energy levels are unique for each element, every gas discharge tube will glow with a distinctive color depending on the identity of the gas (see Figure 7).

Figure 7. Gas discharge tubes are enclosed glass tubes filled with a gas at low pressure through which an electric current is passed. Electrons in the gaseous atoms first become excited, and then fall back to lower energy levels, emitting light of a distinctive color in the process. Shown are gas discharge tubes of helium, neon, argon, krypton, and xenon.
“Neon” signs are familiar examples of gas discharge tubes. However, only signs that glow with the red-orange color seen in the figure are actually filled with neon. Signs of other colors contain different gases or mixtures of gases.
Scientists studied the distinctive pink color of the gas discharge created by hydrogen gas. When a narrow beam of this light was viewed through a prism, the light was separated into four lines of very specific wavelengths (and frequencies since ![]() and
and ![]() are inversely related). An atomic emission spectrum is the pattern of lines formed when light passes through a prism to separate it into the different frequencies of light it contains. Figure 8 shows the atomic emission spectrum of hydrogen.
are inversely related). An atomic emission spectrum is the pattern of lines formed when light passes through a prism to separate it into the different frequencies of light it contains. Figure 8 shows the atomic emission spectrum of hydrogen.
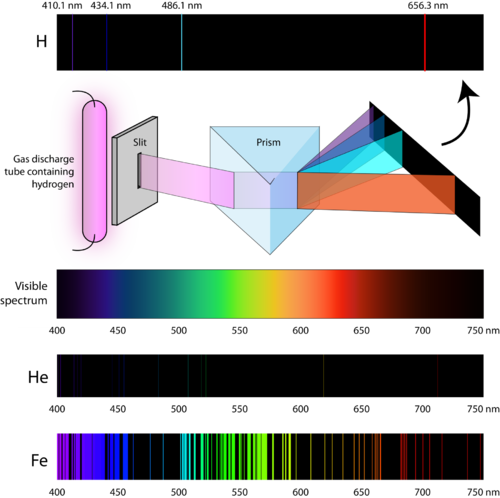
Figure 8. When light from a hydrogen gas discharge tube is passed through a prism, the light is split into four visible lines. Each of these spectral lines corresponds to a different electron transition from a higher energy state to a lower energy state. Every element has a unique atomic emission spectrum, as shown by the examples of mercury (Hg) and strontium (Sr).
Classical theory was unable to explain the existence of atomic emission spectra, also known as line-emission spectra. According to classical physics, a ground state atom would be able to absorb any amount of energy rather than only discrete amounts. Likewise, when the atoms relaxed back to a lower energy state, any amount of energy could be released. This would result in what is known a continuous spectrum , where all wavelengths and frequencies are represented. White light viewed through a prism and a rainbow are examples of continuous spectra. Atomic emission spectra were more proof of the quantized nature of light and led to a new model of the atom based on quantum theory.
Summary
- Atomic emission spectra are produced when excited electrons return to ground state.
- The emitted light corresponds to energies of the specific electrons.
Practice
Use the link below to answer the following questions:
http://chemistry.bd.psu.edu/jircitano/periodic4.html
- How many spectral lines are there for lithium?
- How many spectral lines are there for beryllium?
- Which element would you expect to have more lines: Na or Mg?
Review
- What is the ground state of an atom?
- What is an excited state?
- Why do we see emission lines when electrons return to the ground state?
Glossary
- atomic emission spectrum: The pattern of lines formed when light passes through a prism to separate it into the different frequencies of light it contains.
- continuous spectrum: All wavelengths of light are present.
- excited state: A state where the potential energy of the atom is higher than the ground state.
- ground state: The lowest energy state of the atom.
Bohr’s Atomic Model
How does this worker’s energy change as he climbs up and down the ladder?

Climbing a ladder takes energy. At every step, you are pushing yourself up against gravity, and accumulating potential energy. Coming back down releases that potential energy as you descend step by step. If you are not careful, you can release that potential energy all at once when you fall off the ladder (never a good idea). In addition, you take the climb or descent in steps. There is no “in-between” position on the ladder – your foot either hits a rung or it hits empty space and you are in trouble until you find a rung to stand on.
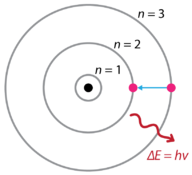
Figure 9. Bohr’s atomic model hydrogen emission spectra.
Following the discoveries of hydrogen emission spectra and the photoelectric effect, the Danish physicist Niels Bohr (1885–1962) proposed a new model of the atom in 1915. Bohr proposed that electrons do not radiate energy as they orbit the nucleus, but exist in states of constant energy which he called stationary states. This means that the electrons orbit at fixed distances from the nucleus (see Figure 9). Bohr’s work was primarily based on the emission spectra of hydrogen. This is also referred to as the planetary model of the atom. It explained the inner workings of the hydrogen atom. Bohr was awarded the Nobel Prize in physics in 1922 for his work.
Bohr explained that electrons can be moved into different orbits with the addition of energy. When the energy is removed, the electrons return back to their ground state, emitting a corresponding amount of energy—a quantum of light, or photon. This was the basis for what later became known as quantum theory. This is a theory based on the principle that matter and energy have the properties of both particles and waves. It accounts for a wide range of physical phenomena, including the existence of discrete packets of energy and matter, the uncertainty principle, and the exclusion principle.
According to the Bohr model, often referred to as a planetary model, the electrons encircle the nucleus of the atom in specific allowable paths called orbits. When the electron is in one of these orbits, its energy is fixed. The ground state of the hydrogen atom, where its energy is lowest, is when the electron is in the orbit that is closest to the nucleus. The orbits that are further from the nucleus are all of successively greater energy. The electron is not allowed to occupy any of the spaces in between the orbits. An everyday analogy to the Bohr model is the rungs of a ladder. As you move up or down a ladder, you can only occupy specific rungs and cannot be in the spaces in between rungs. Moving up the ladder increases your potential energy, while moving down the ladder decreases your energy.
Bohr’s work had a strong influence on our modern understanding of the inner workings of the atom. However, his model worked well for an explanation for the emissions of the hydrogen atom, but was seriously limited when applied to other atoms. Shortly after Bohr published his planetary model of the atom, several new discoveries were made, which resulted in, yet again, a revised view of the atom.
Summary
- The Bohr model postulates that electrons orbit the nucleus at fixed energy levels.
- Orbits further from the nucleus exist at higher energy levels.
- When electrons return to a lower energy level, they emit energy in the form of light.
Practice
Use the link below to answer the following questions:
- How does an electron change orbits?
- What was the Bohr model based on?
- What did Bohr believe about the orbits?
- Does Bohr’s model work for all atoms?
Review
- When did Bohr propose his model of the atom?
- What is a stationary state?
- What is the ground state?
- Can the electron occupy any space between the orbits?
Glossary
- planetary model: A way to describe Bohr’s model of the atom.
- quantum theory: Matter and energy have the properties of both particles and waves.
- stationary state: Electrons orbit at fixed distance from the nucleus.
Spectral Lines of Hydrogen
Learning Objectives
- List the electron transition lines according to energy levels.
- Explain the presence of emission lines and relate them to electron transitions
Can you fix a car engine?
 It’s not as common any more, but there was a time when many people could work on their own cars if there was a problem. Today, engines are computerized and require specialized training and tools in order to be fixed. When people did their own repairs, it was sometimes a trial and error process. Maybe the parks plugs needed to be replaced. No, that didn’t fix the problem completely, but it was a start in the right direction. Science operates the same way. A theory that is developed may work for a while, but then there are data that the theory cannot explain. This means that it’s time for a newer and more inclusive theory.
It’s not as common any more, but there was a time when many people could work on their own cars if there was a problem. Today, engines are computerized and require specialized training and tools in order to be fixed. When people did their own repairs, it was sometimes a trial and error process. Maybe the parks plugs needed to be replaced. No, that didn’t fix the problem completely, but it was a start in the right direction. Science operates the same way. A theory that is developed may work for a while, but then there are data that the theory cannot explain. This means that it’s time for a newer and more inclusive theory.
Bohr’s model explains the spectral lines of the hydrogen atomic emission spectrum. While the electron of the atom remains in the ground state, its energy is unchanged. When the atom absorbs one or more quanta of energy, the electron moves from the ground state orbit to an excited state orbit that is further away. Energy levels are designated with the variable ![]() . The ground state is
. The ground state is ![]() , the first excited state is
, the first excited state is ![]() , and so on. The energy that is gained by the atom is equal to the difference in energy between the two energy levels. When the atom relaxes back to a lower energy state, it releases energy that is again equal to the difference in energy of the two orbits.
, and so on. The energy that is gained by the atom is equal to the difference in energy between the two energy levels. When the atom relaxes back to a lower energy state, it releases energy that is again equal to the difference in energy of the two orbits.
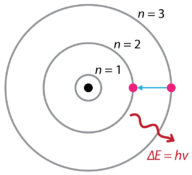
Figure 10. Bohr model of the atom
In Figure 10, electron is shown transitioning from the n = 3 energy level to the n = 2 energy level. The photon of light that is emitted has a frequency that corresponds to the difference in energy between the two levels.
The change in energy, ![]() , then translates to light of a particular frequency being emitted according to the equation
, then translates to light of a particular frequency being emitted according to the equation ![]() . Recall that the atomic emission spectrum of hydrogen had spectral lines consisting of four different frequencies. This is explained in the Bohr model by the realization that the electron orbits are not equally spaced. As the energy increases further and further from the nucleus, the spacing between the levels gets smaller and smaller.
. Recall that the atomic emission spectrum of hydrogen had spectral lines consisting of four different frequencies. This is explained in the Bohr model by the realization that the electron orbits are not equally spaced. As the energy increases further and further from the nucleus, the spacing between the levels gets smaller and smaller.
Based on the wavelengths of the spectral lines, Bohr was able to calculate the energies that the hydrogen electron would have in each of its allowed energy levels. He then mathematically showed which energy level transitions corresponded to the spectral lines in the atomic emission spectrum (Figure 11).
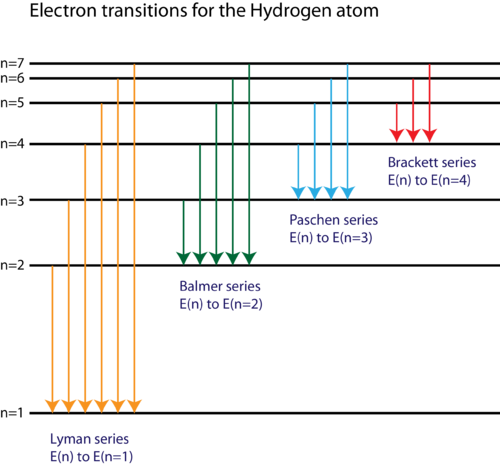
Figure 11. The electron energy level diagram for the hydrogen atom.
He found that the four visible spectral lines corresponded to transitions from higher energy levels down to the second energy level ![]() . This is called the Balmer series. Transitions ending in the ground state
. This is called the Balmer series. Transitions ending in the ground state ![]() are called the Lyman series, but the energies released are so large that the spectral lines are all in the ultraviolet region of the spectrum. The transitions called the Paschen series and the Brackett series both result in spectral lines in the infrared region because the energies are too small.
are called the Lyman series, but the energies released are so large that the spectral lines are all in the ultraviolet region of the spectrum. The transitions called the Paschen series and the Brackett series both result in spectral lines in the infrared region because the energies are too small.
Bohr’s model was a tremendous success in explaining the spectrum of the hydrogen atom. Unfortunately, when the mathematics of the model was applied to atoms with more than one electron, it was not able to correctly predict the frequencies of the spectral lines. While Bohr’s model represented a great advancement in the atomic model and the concept of electron transitions between energy levels is valid, improvements were needed in order to fully understand all atoms and their chemical behavior.
Summary
- Emission lines for hydrogen correspond to energy changes related to electron transitions.
- The Bohr model works only for the hydrogen atom.
Practice
Use the link below to answer the following questions:
http://www.chemguide.co.uk/atoms/properties/hspectrum.html
- How many volts can be used to generate a hydrogen line spectrum?
- Can you see the Lyman series with the naked eye?
- Which series can we at least partially see?
- What happens to the hydrogen gas in a discharge tube?
Review
- What happens when a hydrogen atoms absorbs one or more quanta of energy?
- How do we detect the change in energy?
- What electron transitions are presented by the lines of the Paschen series?
- Does the Bohr model work for atoms other than hydrogen?
Glossary
- electron transition: Movement of an electron from one energy level to another.
de Broglie Wave Equation
Learning Objectives
- State the de Broglie wave equation.
- Use this equation to calculate the wavelength of a moving object.
Bohr’s model of the atom was valuable in demonstrating how electrons were capable of absorbing and releasing energy and how atomic emission spectra were created. However, the model did not really explain why electrons should exist only in fixed circular orbits rather than being able to exist in a limitless number of orbits all with different energies. In order to explain why atomic energy states are quantized, scientists needed to rethink the way in which they viewed the nature of the electron and its movement.
Planck’s investigation of the emission spectra of hot objects and the subsequent studies into the photoelectric effect had proven that light was capable of behaving both as a wave and as a particle. It seemed reasonable to wonder if electrons could also have a dual wave-particle nature. In 1924, French scientist Louis de Broglie (1892–1987) derived an equation that described the wave nature of any particle. Particularly, the wavelength (λ) of any moving object is given by:
[latex]\lambda = \frac{h}{mv}[/latex]
In this equation, h is Planck’s constant, ![]() is the mass of the particle in kg, and v is the velocity of the particle in m/s. The problem below shows how to calculate the wavelength of the electron.
is the mass of the particle in kg, and v is the velocity of the particle in m/s. The problem below shows how to calculate the wavelength of the electron.
Sample Problem: de Broglie Wave Equation
An electron of mass 9.11 × 10 -31 kg moves at nearly the speed of light. Using a velocity of 3.00 × 10 8 m/s, calculate the wavelength of the electron.
Step 1: List the known quantities and plan the problem.
Known
- mass
 = 9.11 × 10 -31 kg
= 9.11 × 10 -31 kg - Planck’s constant
 = 6.6262 10 -34 × J • s
= 6.6262 10 -34 × J • s - velocity
 = 3.00 × 10 8 m/s
= 3.00 × 10 8 m/s
Unknown
- wavelength

Apply the de Broglie wave equation [latex]\lambda = \frac{h}{mv}[/latex] to solve for the wavelength of the moving electron.
Step 2: Calculate
![]()
Step 3: Think about your result.
This very small wavelength is about 1/20th of the diameter of a hydrogen atom. Looking at the equation, as the speed of the electron decreases, its wavelength increases. The wavelengths of everyday large objects with much greater masses should be very small.
If we were to calculate the wavelength of a 0.145 kg baseball thrown at a speed of 40 m/s, we would come up with an extremely short wavelength on the order of 10 -34 m. This wavelength is impossible to detect even with advanced scientific equipment. Indeed, while all objects move with wavelike motion, we never notice it because the wavelengths are far too short. On the other hand, particles with measurable wavelengths are all very small. However, the wave nature of the electron proved to be a key development in a new understanding of the nature of the electron. An electron that is confined to a particular space around the nucleus of an atom can only move around that atom in such a way that its electron wave “fits” the size of the atom correctly. This means that the frequencies of electron waves are quantized . Based on the ![]() equation, the quantized frequencies means that electrons can only exist in an atom at specific energies, as Bohr had previously theorized.
equation, the quantized frequencies means that electrons can only exist in an atom at specific energies, as Bohr had previously theorized.
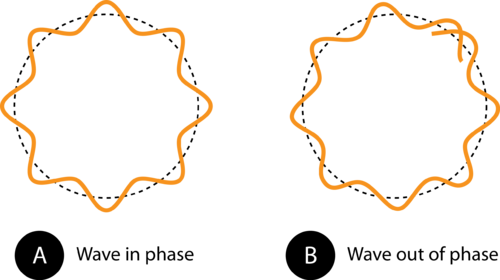
Figure 12. The circumference of the orbit in (A) allows the electron wave to fit perfectly into the orbit. This is an allowed orbit. In (B), the electron wave does not fit properly into the orbit, so this orbit is not allowed.
Summary
- The deBroglie wave equations allows calculation of the wavelength of any moving object.
- As the speed of the electron decreases, its wavelength increases.
Practice
Use the link below to practice calculations using the deBroglie wave equation:
Review
- What did the Bohr model not explain?
- State the deBroglie wave equation.
- What happens as the speed of the electron decreases?
Glossary
- de Broglie wave equation: [latex]\lambda = \frac{h}{mv}[/latex] .
- quantize: Limit the possible values of (a magnitude or quantity) to a discrete set of values by quantum mechanical rules.
Quantum Mechanics
How do you study something that seemingly makes no sense? We talk about electrons being in orbits and it sounds like we can tell where that electron is at any moment. We can draw pictures of electrons in orbit, but the reality is that we just don’t know exactly where they are. We are going to take a quick look at an area of science that even leaves scientists puzzled. When asked about quantum mechanics, Niels Bohr (who proposed the Bohr model of the atom) said: “Anyone who is not shocked by quantum theory has not understood it”. Richard Feynman (one of the founders of modern quantum theory) stated: “I think I can safely say that nobody understands quantum theory”. So, let’s take a short trip into a land that challenges our every-day world.
The study of motion of large objects such as baseballs is called mechanics, or more specifically classical mechanics. Because the quantum nature of the electron and other tiny particles moving at high speeds, classical mechanics is inadequate to accurately describe their motion.

Figure 13. Erwin Schrödinger
Quantum mechanics is the study of the motion of objects that are atomic or subatomic in size and thus demonstrate wave-particle duality. In classical mechanics, the size and mass of the objects involved effectively obscures any quantum effects so that such objects appear to gain or lose energies in any amounts. Particles whose motion is described by quantum mechanics gain or lose energy in the small pieces called quanta.
One of the fundamental (and hardest to understand) principles of quantum mechanics is that the electron is both a particle and a wave. In the everyday macroscopic world of things we can see, something cannot be both. But this duality can exist in the quantum world of the submicroscopic at the atomic scale.
At the heart of quantum mechanics is the idea that we cannot specify accurately the location of an electron. All we can say is that there is a probability that it exists within this certain volume of space. The scientist Erwin Schrödinger developed an equation that deals with these calculations, which we will not pursue at this time.
Summary
- Quantum mechanics involves the study of material at the atomic level.
- This field deals with probabilities since we cannot definitely locate a particle.
Practice
Use the link below to answer the following questions:
http://www.nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-bio.html
- What were the scientific interests of Schrödinger’s father?
- When did Schrödinger discover his wave equation?
- What award did he receive for this work?
- In what other areas did Schrödinger carry out research?
Review
- What does quantum mechanics deal with?
- How would you describe an electron?
- What did Schrödinger demonstrate about the location of a particle?
Glossary
- quanta: Plural of quantum, smallest amount of energy that can exist independently.
- quantum mechanics: The study of the motion of objects that are atomic or subatomic in size and thus demonstrate wave-particle duality.
Heisenberg Uncertainty Principle
Learning Objectives
State the Heisenberg Uncertainty Principle.
What are the different uses of lasers?

Lasers have numerous applications outside the physics lab. These devices can be employed to measure distances accurately and many commercial instruments are used in construction for laying out a building site. When the light beam strikes a solid object, it is reflected back and the device determines how far away the object is. There is such a significant difference between the mass of the light beam (photons) and the mass of the object, the beam does not disturb the object at all. One measurement of interest was the use of a laser to measure the distance from the Earth to the moon (see figure above). The impact of the photons from the laser on the moon had absolutely no effect on the moon’s orbit.
Another feature that is unique to quantum mechanics is the uncertainty principle. The Heisenberg Uncertainty Principle states that it is impossible to determine simultaneously both the position and the velocity of a particle. The detection of an electron, for example, would be made by way of its interaction with photons of light. Since photons and electrons have nearly the same energy, any attempt to locate an electron with a photon will knock the electron off course, resulting in uncertainty about where the electron is located (see Figure below ). We do not have to worry about the uncertainty principle with large everyday objects because of their mass. If you are looking for something with a flashlight, the photons coming from the flashlight are not going to cause the thing you are looking for to move. This is not the case with atomic-sized particles, leading scientists to a new understanding about how to envision the location of the electrons within atoms.
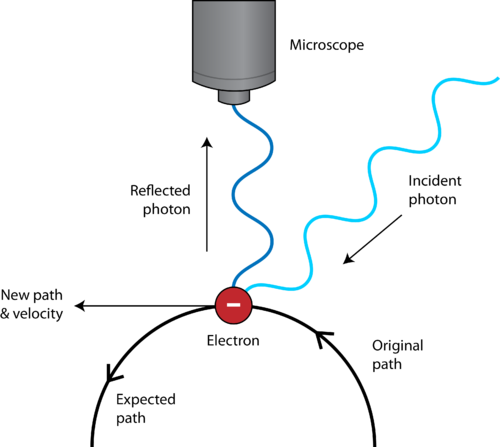
Figure 14. Heisenberg Uncertainty Principle: The observation of an electron with a microscope requires reflection of a photon off of the electron. This reflected photon causes a change in the path of the electron.
Summary
- The Heisenberg Uncertainty principle explains why we cannot simultaneously determine both the precise velocity and position of a particle.
- This principle is only applicable at the atomic level.
Practice
Use the link below to answer the following questions:
- When did Heisenberg get his Ph.D?
- What idea of Niels Bohr did Heisenberg disprove?
- When did he win his Nobel Prize?
Review
- Why is the Heisenberg Uncertainty Principle true at the atomic level?
- Is the principle valid at the macroscopic level?
Glossary
- Heisenberg Uncertainty Principle: It is impossible to determine simultaneously both the position and the velocity of a particle.
Quantum Mechanical Atomic Model
Examples
The news flash interrupts your favorite TV program. “There has been a hold-up at the First National Bank. The suspect fled in a car and is believed to be somewhere in the downtown district. Everyone is asked to be on the alert.” The robber can be located only within a certain area – the police do not have an exact location, just a general idea as to the whereabouts of the thief.
In 1926, Austrian physicist Erwin Schrödinger (1887–1961) used the wave-particle duality of the electron to develop and solve a complex mathematical equation that accurately described the behavior of the electron in a hydrogen atom. The quantum mechanical model of the atom comes from the solution to Schrödinger’s equation. Quantization of electron energies is a requirement in order to solve the equation. This is unlike the Bohr model, in which quantization was simply assumed with no mathematical basis.
Recall that in the Bohr model, the exact path of the electron was restricted to very well-defined circular orbits around the nucleus. The quantum mechanical model is a radical departure from that. Solutions to the Schrödinger wave equation, called wave functions, give only the probability of finding an electron at a given point around the nucleus. Electrons do not travel around the nucleus in simple circular orbits.
The location of the electrons in the quantum mechanical model of the atom is often referred to as an electron cloud . The electron cloud can be thought of in the following way: Imagine placing a square piece of paper on the floor with a dot in the circle representing the nucleus. Now take a marker and drop it onto the paper repeatedly, making small marks at each point the marker hits. If you drop the marker many, many times, the overall pattern of dots will be roughly circular. If you aim toward the center reasonably well, there will be more dots near the nucleus and progressively fewer dots as you move away from it. Each dot represents a location where the electron could be at any given moment. Because of the uncertainty principle, there is no way to know exactly where the electron is. An electron cloud has variable densities: a high density where the electron is most likely to be and a low density where the electron is least likely to be (Figure 15).
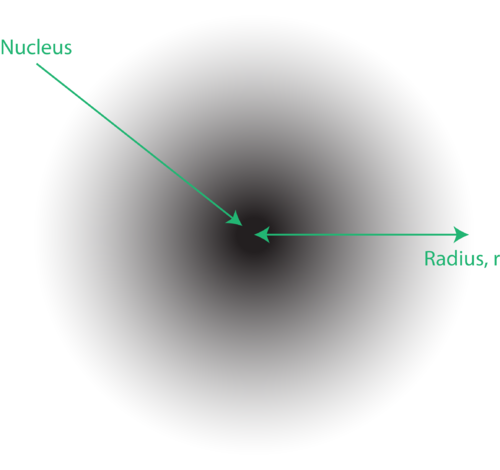
Figure 15. An electron cloud: the darker region nearer the nucleus indicates a high probability of finding the electron, while the lighter region further from the nucleus indicates a lower probability of finding the electron.
In order to specifically define the shape of the cloud, it is customary to refer to the region of space within which there is a 90% probability of finding the electron. This is called an orbital , the three-dimensional region of space that indicates where there is a high probability of finding an electron.
Summary
- The Schrödinger wave equation replaced the Bohr ideas about electron location with an uncertainty factor.
- The location of the electron can only be given as a probability that the electron is somewhere in a certain area.
Practice
Use the link below to answer the following questions:
http://science.howstuffworks.com/atom8.htm
- What was one problem with the Bohr model of the atom?
- What did Heisenberg show about electrons?
- What did Schrödinger derive?
Review
- What does the quantum mechanical view of the atom require?
- What is a wave function?
- What does a high density electron cloud suggest?
Glossary
- electron cloud: The location of the electrons in the quantum mechanical model of the atom.
- orbital: The three-dimensional region of space that indicates where there is a high probability of finding an electron.
- quantum mechanical model: A model of the atom that derives from the Schrödinger wave equation and deals with probabilities.
- wave function: Give only the probability of finding an electron at a given point around the nucleus.
Quantum Numbers
Learning Objectives
- Define the four quantum numbers.
- Determine quantum numbers for specific electrons when given appropriate data.
Can you guess how many people are in this stadium?

If you attend a college or professional football game, you need a ticket to get in. It is very likely that your ticket may specify a gate number, a section number, a row, and a seat number. No other ticket can have the same four parts to it. It may have the same gate, section, and seat number, but it would have to be in a different row. Each seat is unique and allows only one occupant to fill it.
We use a series of specific numbers, called quantum numbers, to describe the location of an electron in an associated atom. Quantum numbers specify the properties of the atomic orbitals and the electrons in those orbitals. An electron in an atom or ion has four quantum numbers to describe its state. Think of them as important variables in an equation which describes the three-dimensional position of electrons in a given atom.
Principal Quantum Number [latex](n)[/latex]
The principal quantum number, signified by [latex](n)[/latex], is the main energy level occupied by the electron. Energy levels are fixed distances from the nucleus of a given atom. They are described in whole number increments (e.g., 1, 2, 3, 4, 5, 6, …). At location ![]() , an electron would be closest to the nucleus, while
, an electron would be closest to the nucleus, while ![]() the electron would be farther, and
the electron would be farther, and ![]() farther yet. As we will see, the principal quantum number corresponds to the row number for an atom on the periodic table.
farther yet. As we will see, the principal quantum number corresponds to the row number for an atom on the periodic table.
Angular Momentum Quantum Number [latex](l)[/latex]
The angular momentum quantum number , signified as [latex](l)[/latex], describes the general shape or region an electron occupies—its orbital shape. The value of l depends on the value of the principle quantum number n. The angular momentum quantum number can have positive values of zero to ![]() . If
. If ![]() ,
, ![]() could be either 0 or 1.
could be either 0 or 1.
Magnetic Quantum Number [latex](m_l)[/latex]
The magnetic quantum number, signified as [latex](m_l)[/latex], describes the orbital orientation in space. Electrons can be situated in one of three planes in three dimensional space around a given nucleus ![]() and
and ![]() . For a given value of the angular momentum quantum number l, there can be
. For a given value of the angular momentum quantum number l, there can be ![]() values for [latex](m_l)[/latex]. As an example:
values for [latex](m_l)[/latex]. As an example:
![]()
![]() or 1
or 1
for ![]()
for ![]()
| Principal energy level | Number of possible sublevels | Possible Angular Momentum Quantum Numbers | Orbital Designation by Principal Energy Level and Sublevel |
| 1 | 1 s | ||
| 2 |
|
2 s
2 p |
|
| 3 |
|
3 s
3 p 3 d |
|
| 4 |
|
4 s
4 p 4 d 4 f |
Table above shows the possible magnetic quantum number values [latex](m_l)[/latex] for the corresponding angular momentum quantum numbers [latex](l)[/latex] of ![]() and
and ![]() .
.
Spin Quantum Number [latex](m_s)[/latex]
The spin quantum number describes the spin for a given electron. An electron can have one of two associated spins, ![]() spin, or
spin, or ![]() spin. An electron cannot have zero spin. We also represent spin with arrows
spin. An electron cannot have zero spin. We also represent spin with arrows ![]() or
or ![]() . A single orbital can hold a maximum of two electrons and each must have opposite spin.
. A single orbital can hold a maximum of two electrons and each must have opposite spin.
Summary
- Quantum numbers specify the arrangements of electrons in orbitals.
- There are four quantum numbers that provide information about various aspects of electron behavior.
Practice
Watch the video, pause at each question and try to calculate the quantum number before you see the answer written in. Do not try to answer the orbital questions, just the quantum number ones.
Review
- What do quantum numbers do?
- What is the principal quantum number?
- What does the spin quantum number represent?
Glossary
- angular momentum quantum number [latex](l)[/latex]: Describes the general region occupied by the electron.
- magnetic quantum number [latex](m_l)[/latex]: Describes the orbital orientation of the electron in space.
- principal quantum number [latex](n)[/latex]: Specifies the main energy level occupied by the electron.
- quantum numbers: Describe the location of an electron in an atom.
- spin quantum number [latex](m_s)[/latex]: Describes the spin for a given electron.
Orbitals
Learning Objectives
- Draw the shapes of s , p , d , and f orbitals.
- Relate the four quantum numbers for an electron to a specific orbital.
How is it that so many planes are able to fly without running into each other?

The flight path of a commercial airliner is carefully regulated by the Federal Aviation Administration. Each airplane must maintain a distance of five miles from another plane flying at the same altitude and 2,000 feet above and below another aircraft (1,000 feet if the altitude is less than 29,000 feet). So, each aircraft only has certain positions it is allowed to maintain while it flies. As we explore quantum mechanics, we see that electrons have similar restrictions on their locations.
We can apply our knowledge of quantum numbers to describe the arrangement of electrons for a given atom. We do this with something called electron configurations. They are effectively a map of the electrons for a given atom. We look at the four quantum numbers for a given electron and then assign that electron to a specific orbital.
s Orbitals
For any value of n, a value of ![]() places that electron in an s orbital. This orbital is spherical in shape:
places that electron in an s orbital. This orbital is spherical in shape:

p Orbitals
From Table below we see that we can have three possible orbitals when ![]() . These are designated as p orbitals and have dumbbell shapes. Each of the p orbitals has a different orientation in three-dimensional space.
. These are designated as p orbitals and have dumbbell shapes. Each of the p orbitals has a different orientation in three-dimensional space.

d Orbitals
When ![]() ,
, ![]() values can be -2, -1, 0, +1, +2 for a total of five d orbitals . Note that all five of the orbitals have specific three-dimensional orientations.
values can be -2, -1, 0, +1, +2 for a total of five d orbitals . Note that all five of the orbitals have specific three-dimensional orientations.

f Orbitals
The most complex set of orbitals are the f orbitals . When ![]() ,
, ![]() values can be -3, -2, -1, 0, +1, +2, +3 for a total of seven different orbital shapes. Again, note the specific orientations of the different f orbitals.
values can be -3, -2, -1, 0, +1, +2, +3 for a total of seven different orbital shapes. Again, note the specific orientations of the different f orbitals.

| Principal Quantum Number |
Allowable Sublevels | Number of Orbitals per Sublevel | Number of Orbitals per Principal Energy Level | Number of Electrons per Sublevel | Number of Electrons per Principal Energy Level |
| 1 | s | 1 | 1 | 2 | 2 |
| 2 | s
p |
1
3 |
4 | 2
6 |
8 |
| 3 | s
p d |
1
3 5 |
9 | 2
6 10 |
18 |
| 4 | s
p d f |
1
3 5 7 |
16 | 2
6 10 14 |
32 |
Summary
- There are four different classes of electron orbitals.
- These orbitals are determined by the value of the angular momentum quantum number l.
Practice
Use the link below to answer the following questions:
http://www.chem4kids.com/files/atom_orbital.html
- What is a shell?
- What do the letters K-Q stand for?
- How many electrons does the K shell hold?
- What is the maximum number of electrons any shell can hold?
Review
- What is an electron configuration?
- How many electrons are in the
 orbital?
orbital? - What is the total number of electrons in a p orbital?
- How many electrons does it take to completely fill a d orbital?
Glossary
- electron configuration: A map of the electrons for a given atom.
- d orbital: Five orbitals characterized by
 .
. - f orbitals: The most complex set of orbitals with seven orbital shapes for
 .
. - p orbitals: Three dumbbell shaped orbitals for
 .
. - s orbitals: Spherical orbitals where
 .
.
Aufbau Principle
Learning Objectives
- State the Aufbau principle.
- Use the Aufbau principle to determine the electron configuration of an atom.
How are buildings constructed?

Construction of a building begins at the bottom. The foundation is laid and the building goes up step by step. You obviously cannot start with the roof since there is no place to hang it. The building goes from the lowest level to the highest level in a systematic way.
In order to create ground state electron configurations for any element, it is necessary to know the way in which the atomic sublevels are organized in order of increasing energy. The Figure below shows the order of increasing energy of the sublevels.
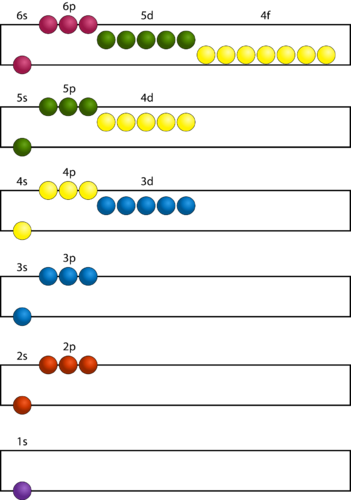
Figure 16. Electrons are added to atomic orbitals in order from low energy (bottom of graph) to high (top of graph) according to the Aufbau principle. Principal energy levels are color coded, while sublevels are grouped together and each circle represents an orbital capable of holding two electrons.
The lowest energy sublevel is always the 1 s sublevel, which consists of one orbital. The single electron of the hydrogen atom will occupy the 1 s orbital when the atom is in its ground state. As we proceed with atoms with multiple electrons, those electrons are added to the next lowest sublevel: 2 s , 2 p , 3 s , and so on. The Aufbau principle states that an electron occupies orbitals in order from lowest energy to highest. The Aufbau (German: “building up, construction”) principle is sometimes referred to as the “building-up” principle. It is worth noting that in reality atoms are not built by adding protons and electrons one at a time and that this method is merely an aid for us to understand the end result.
As seen in the Figure above , the energies of the sublevels in different principal energy levels eventually begin to overlap. After the 3 p sublevel, it would seem logical that the 3 d sublevel should be the next lowest in energy. However, the 4 s sublevel is slightly lower in energy than the 3 d sublevel and thus fills first. Following the filling of the 3 d sublevel is the 4 p , then the 5 s and the 4 d . Note that the 4 f sublevel does not fill until just after the 6 s sublevel. The Figure below is a useful and simple aid for keeping track of the order of fill of the atomic sublevels.

Figure 17. The Aufbau principle is illustrated in the diagram by following each red arrow in order from top to bottom: 1s, 2s, 2p, 3s, etc.
Summary
- The Aufbau principle gives the order of electron filling in an atom.
- It can be used to describe the locations and energy levels of every electron in a given atom.
Practice
Use the link below to answer the following questions:
http://ths.talawanda.net/~BrambleN/classroom/Chemistry/Notes/Section%202A/Exceptions&Shortcut.htm
- Do the electrons in all atoms follow the Aufbau rule?
- What happens to electrons in copper to make the atom more stable?
- How does silver become more stable?
Review
- What is the Aufbau principle?
- Which orbital is filled after the 2 p ?
- Which orbital is filled after 4 s ?
- Which orbital is filled after 6 s ?
Glossary
- Aufbau principle: An electron occupies orbitals in order from lowest energy to highest.
Pauli Exclusion Principle
Learning Objectives
State the Pauli exclusion principle.
Can you name one thing that easily distinguishes you from the rest of the world?
And we’re not talking about DNA – that’s a little expensive to sequence. For many people, it is their email address. My email address allows people all over the world to contact me. It does not belong to anyone else, but serves to identify me. Electrons also have a unique set of identifiers in the quantum numbers that describe their location and spin.
When we look at the orbital possibilities for a given atom, we see that there are different arrangements of electrons for each different type of atom. Since each electron must maintain its unique identity, we intuitively sense that the four quantum numbers for any given electron must not match up exactly with the four quantum numbers for any other electron in that atom.
For the hydrogen atom, there is no problem since there is only one electron in the H atom. However, when we get to helium we see that the first three quantum numbers for the two electrons are the same: same energy level, same spherical shape. What differentiates the two helium electrons is their spin. One of the electrons has ![]() spin while the other electron has
spin while the other electron has ![]() spin. So the two electrons in the 1s orbital are each unique and distinct from one another because their spins are different. This observation leads to the Pauli exclusion principle , which states that no two electrons in an atom can have the same set of four quantum numbers. The energy of the electron is specified by the principal, angular momentum, and magnetic quantum numbers. If those three numbers are identical for two electrons, the spin numbers must be different in order for the two electrons to be differentiated from one another. The two values of the spin quantum number allow each orbital to hold two electrons. The figure below shows how the electrons are indicated in a diagram.
spin. So the two electrons in the 1s orbital are each unique and distinct from one another because their spins are different. This observation leads to the Pauli exclusion principle , which states that no two electrons in an atom can have the same set of four quantum numbers. The energy of the electron is specified by the principal, angular momentum, and magnetic quantum numbers. If those three numbers are identical for two electrons, the spin numbers must be different in order for the two electrons to be differentiated from one another. The two values of the spin quantum number allow each orbital to hold two electrons. The figure below shows how the electrons are indicated in a diagram.
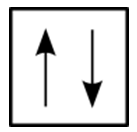
Figure 18
In an orbital filling diagram, a square represents an orbital, while arrows represent electrons. An arrow pointing upward represents one spin direction, while an arrow pointing downward represents the other spin direction.
Summary
- The Pauli exclusion principle specifies limits on how identical quantum numbers can be for two electrons in the same atom.
Practice
Use the link below to answer the following questions:
http://www.nobelprize.org/nobel_prizes/physics/laureates/1945/pauli-bio.html
- When was Pauli born?
- How old was he when he received his doctorate?
- What was he the first to recognize?
- When did he win his Nobel Prize in Physics?
Review
- What is the difference between the two helium electrons?
- What does the Pauli exclusion principle state?
- What does the two values for the spin quantum number allow?
Glossary
- Pauli exclusion principle: No two electrons in an atom can have the same set of four quantum numbers.
Hund’s Rule and Orbital Filling Diagrams
Learning Objectives
- State Hund’s rule.
- Apply Hund’s rule to the filling of orbitals.
- Use orbital filling diagrams to describe the locations of electrons in an atom.
Have you ever wondered what those load limit signs mean on a bridge?

The sign above says that nothing over five tons is allowed because it will do damage to the structure. There are limits to the amount of weight that a bridge can support, there are limits to the number of people that can safely occupy a room, and there are limits to what can go into an electron orbital.
Hund’s Rule
The last of the three rules for constructing electron arrangements requires electrons to be placed one at a time in a set of orbitals within the same sublevel. This minimizes the natural repulsive forces that one electron has for another. Hund’s rule states that orbitals of equal energy are each occupied by one electron before any orbital is occupied by a second electron and that each of the single electrons must have the same spin. The Figure below shows how a set of three p orbitals is filled with one, two, three, and four electrons.
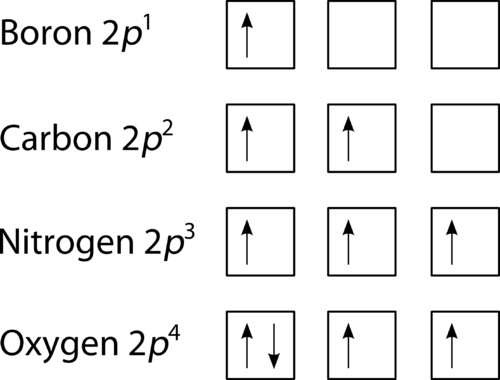
Figure 19. The 2p sublevel, for the elements boron (Z = 5), carbon (Z = 6), nitrogen (Z = 7), and oxygen (Z = 8). According to Hund’s rule, as electrons are added to a set of orbitals of equal energy, one electron enters each orbital before any orbital receives a second electron.
Orbital Filling Diagrams
An orbital filling diagram is the more visual way to represent the arrangement of all the electrons in a particular atom. In an orbital filling diagram, the individual orbitals are shown as circles (or squares) and orbitals within a sublevel are drawn next to each other horizontally. Each sublevel is labeled by its principal energy level and sublevel. Electrons are indicated by arrows inside the circles. An arrow pointing upwards indicates one spin direction, while a downward pointing arrow indicates the other direction. The orbital filling diagrams for hydrogen, helium, and lithium are shown in Figure below .
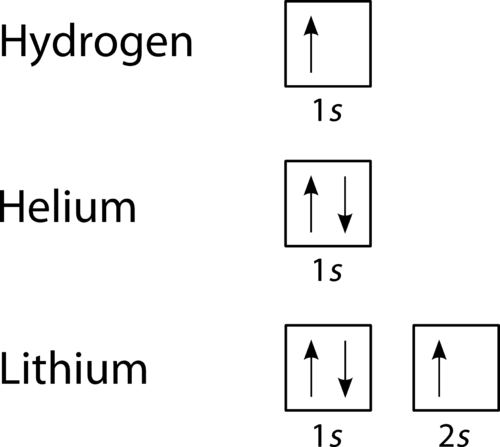
Figure 20. Orbital filling diagrams for hydrogen, helium, and lithium.
According to the Aufbau process, sublevels and orbitals are filled with electrons in order of increasing energy. Since the s sublevel consists of just one orbital, the second electron simply pairs up with the first electron as in helium. The next element is lithium and necessitates the use of the next available sublevel, the 2 s .
The filling diagram for carbon is shown in the Figure below . There are two 2 p electrons for carbon and each occupies its own 2 p orbital.
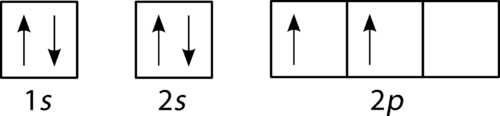
Figure 21. Orbital filling diagram for carbon.
Oxygen has four 2 p electrons. After each 2 p orbital has one electron in it, the fourth electron can be placed in the first 2 p orbital with a spin opposite that of the other electron in that orbital.
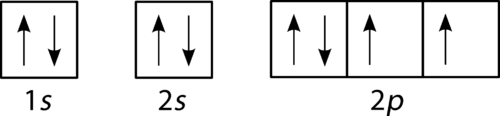
Figure 22. Orbital filling diagram for oxygen.
Summary
- Hund’s rule specifies the order of electron filling within a set of orbitals.
- Orbital filling diagrams are a way of indicating electron locations in orbitals.
Review
- State Hund’s rule.
- What is an orbital filling diagram?
- Is the diagram in the Figure below correct? Explain your answer.

- Is the diagram in the Figure below correct? Explain your answer.

Glossary
- Hund’s rule: Orbitals of equal energy are each occupied by one electron before any orbital is occupied by a second electron and that each of the single electrons must have the same spin.
- orbital filling diagram: A visual way to represent the arrangement of all the electrons in a particular atom.
Electron Configurations
Learning Objectives
Use electron configuration notation to indicate the electron configuration of an atom.
How big is a file?

If you keep your papers in manila folders, you can pick up a folder and see how much it weighs. If you want to know how many different papers (articles, bank records, or whatever else you keep in a folder), you have to take everything out and count. A computer directory, on the other hand, tells you exactly how much you have in each file. We can get the same information on atoms. If we use an orbital filling diagram, we have to count arrows. When we look at electron configuration data, we simply add up the numbers.
Electron configuration notation eliminates the boxes and arrows of orbital filling diagrams. Each occupied sublevel designation is written followed by a superscript that is the number of electrons in that sublevel. For example, the hydrogen configuration is 1 s 1 , while the helium configuration is 1 s 2 . Multiple occupied sublevels are written one after another. The electron configuration of lithium is 1 s 2 2 s 1 . The sum of the superscripts in an electron configuration is equal to the number of electrons in that atom, which is in turn equal to its atomic number.
Sample Problem: Orbital Filling Diagrams and Electron Configurations
Draw the orbital filling diagram for carbon and write its electron configuration.
Step 1: List the known quantities and plan the problem.
Known
- atomic number of carbon, Z = 6
Use the order of fill diagram to draw an orbital filling diagram with a total of six electrons. Follow Hund’s rule. Write the electron configuration.
Step 2: Construct Diagram

Electron configuration 1 s 2 2 s 2 2 p 2
Step 3: Think about your result.
Following the 2 s sublevel is the 2 p , and p sublevels always consist of three orbitals. All three orbitals need to be drawn even if one or more is unoccupied. According to Hund’s rule, the sixth electron enters the second of those p orbitals and with the same spin as the fifth electron.
Second Period Elements
Periods refer to the horizontal rows of the periodic table. Looking at a periodic table you will see that the first period contains only the elements hydrogen and helium. This is because the first principal energy level consists of only the s sublevel and so only two electrons are required in order to fill the entire principal energy level. Each time a new principal energy level begins, as with the third element lithium, a new period is started on the periodic table. As one moves across the second period, electrons are successively added. With beryllium (Z = 4), the 2 s sublevel is complete and the 2 p sublevel begins with boron (Z = 5). Since there are three 2 p orbitals and each orbital holds two electrons, the 2 p sublevel is filled after six elements. The Table below shows the electron configurations of the elements in the second period.
| Element Name | Symbol | Atomic Number | Electron Configuration |
| Lithium | Li | 3 | 1 s 2 2 s 1 |
| Beryllium | Be | 4 | 1 s 2 2 s 2 |
| Boron | B | 5 | 1 s 2 2 s 2 2 p 1 |
| Carbon | C | 6 | 1 s 2 2 s 2 2 p 2 |
| Nitrogen | N | 7 | 1 s 2 2 s 2 2 p 3 |
| Oxygen | O | 8 | 1 s 2 2 s 2 2 p 4 |
| Fluorine | F | 9 | 1 s 2 2 s 2 2 p 5 |
| Neon | Ne | 10 | 1 s 2 2 s 2 2 p 6 |
Summary
- Electron configuration notation simplifies the indication of where electrons are located in a specific atom.
- Superscripts are used to indicate the number of electrons in a given sublevel.
Practice
Use the link below to practice solving electron configuration problems.
http://www.sciencegeek.net/Chemistry/taters/Unit2ElectronNotations.htm
Review
- What does electron configuration notation eliminate?
- How do we know how many electrons are in each sublevel?
- An atom has the electron configuration of 1 s2 2 s2 2 p5 . How many electrons are in that atom?
- Which element has the electron configuration of 1 s2 2 s2 2 p 6 3 s2 ?
Glossary
- electron configuration notation: Each occupied sublevel designation is written followed by a superscript that is the number of electrons in that sublevel.
Valence Electrons
Learning Objectives
- Define valence electron.
- Be able to indicate valence electrons when given the electron configuration for an atom.
What makes a particular element very reactive and another element non-reactive?

A chemical reaction involves either electron removal, electron addition, or electron sharing. The path a specific element will take depends on where the electrons are in the atom and how many there are.
| Element Name | Symbol | Atomic Number | Electron Configuration |
| Lithium | Li | 3 | 1 s 2 2 s 1 |
| Beryllium | Be | 4 | 1 s 2 2 s 2 |
| Boron | B | 5 | 1 s 2 2 s 2 2 p 1 |
| Carbon | C | 6 | 1 s 2 2 s 2 2 p 2 |
| Nitrogen | N | 7 | 1 s 2 2 s 2 2 p 3 |
| Oxygen | O | 8 | 1 s 2 2 s 2 2 p 4 |
| Fluorine | F | 9 | 1 s 2 2 s 2 2 p 5 |
| Neon | Ne | 10 | 1 s 2 2 s 2 2 p 6 |
In the study of chemical reactivity, we will find that the electrons in the outermost principal energy level are very important and so they are given a special name. Valence electrons are the electrons in the highest occupied principal energy level of an atom. In the second period elements listed above, the two electrons in the 1 s sublevel are called inner-shell electrons and are not involved directly in the element’s reactivity or in the formation of compounds. Lithium has a single electron in the second principal energy level and so we say that lithium has one valence electron. Beryllium has two valence electrons. How many valence electrons does boron have? You must recognize that the second principal energy level consists of both the 2 s and the 2 p sublevels and so the answer is three. In fact, the number of valence electrons goes up by one for each step across a period until the last element is reached. Neon, with its configuration ending in s 2p 6 , has eight valence electrons.
Summary
- Valence electrons are the outer-shell electrons of an atom.
- Valence electrons determine the reactivity of an atom.
Practice
Use the link below to answer questions about valence electrons:
http://www.sciencegeek.net/Chemistry/taters/Unit3ValenceElectrons.htm
Review
- Define valence electron.
- Define inner shell electron.
- How many valence electrons are there in fluorine?
- What are the 2 s electrons in nitrogen?
- How many inner shell electrons are there in beryllium?
Glossary
- inner-shell electrons: Those electrons that are not in the outer shell and are not involved in the reactivity of the element.
- valence electrons: The electrons in the highest occupied principal energy level of an atom.
Noble Gas Configuration
Learning Objectives
Use the noble gas configuration approach to write electron configurations for the elements.
How does it feel to be full after a meal?

You had a great meal, but cannot put another bite in your mouth because there is no place for it to go. The noble gases have the same problem – there is no room for any more electrons in their outer shells. They are completely full and cannot handle any more.
Sodium, element number eleven, is the first element in the third period of the periodic table. Its electron configuration is 1 s 2 2 s 2 2 p 6 3 s 1 . The first ten electrons of the sodium atom are the inner-shell electrons and the configuration of just those ten electrons is exactly the same as the configuration of the element neon (Z = 10). This provides the basis for a shorthand notation for electron configurations called the noble gas configuration. The elements that are found in the last column of the periodic table are an important group of elements that are called the noble gases. They are helium, neon, argon, krypton, xenon, and radon. A noble gas configuration of an atom consists of the elemental symbol of the last noble gas prior to that atom, followed by the configuration of the remaining electrons. So for sodium, we make the substitution of [Ne] for the 1 s 2 2 s 2 2 p 6 part of the configuration. Sodium’s noble gas configuration becomes [Ne]3 s 1 . Table below shows the noble gas configurations of the third period elements.
| Element Name | Symbol | Atomic Number | Noble Gas Electron Configuration |
| Sodium | Na | 11 | [Ne]3 s 1 |
| Magnesium | Mg | 12 | [Ne]3 s 2 |
| Aluminum | Al | 13 | [Ne]3 s 2 3 p 1 |
| Silicon | Si | 14 | [Ne]3 s 2 3 p 2 |
| Phosphorus | P | 15 | [Ne]3 s 2 3 p 3 |
| Sulfur | S | 16 | [Ne]3 s 2 3 p 4 |
| Chlorine | Cl | 17 | [Ne]3 s 2 3 p 5 |
| Argon | Ar | 18 | [Ne]3 s 2 3 p 6 |
Again, the number of valence electrons increases from one to eight across the third period.
The fourth and subsequent periods follow the same pattern except for using a different noble gas. Potassium has nineteen electrons, one more than the noble gas argon, so its configuration could be written as [Ar]4 s 1 . In a similar fashion, strontium has two more electrons than the noble gas krypton, which would allow us to write its electrons distribution as [Kr]5 s 2 . All the elements can be represented in this fashion.
Summary
- The noble gas configuration system allows some shortening of the total electron configuration by using the symbol for the noble gas of the previous period as part of the pattern of electrons.
Practice
Use the link below to practice writing noble gas configurations:
http://www.sciencegeek.net/Chemistry/taters/Unit2ElectronNotations.htm
Review
- What is the element represented by [Ne]3 s 2 3 p 2 ?
- What element has this electron configuration [Ar]3 d 7 4 s 2 ?
- What noble gas would be part of the electron configuration notation for Mn?
- How would you write the electron configuration for Ba?
Glossary
- noble gas configuration: Consists of the elemental symbol of the last noble gas prior to that atom, followed by the configuration of the remaining electrons.
Candela Citations
- Chemistry Concepts Intermediate. Authored by: Calbreath, Baxter, et al.. Provided by: CK12.org. Located at: http://www.ck12.org/book/CK-12-Chemistry-Concepts-Intermediate/. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike