Learning Outcomes
- Explain the meaning of solving a system of three variable linear equations
- Explain one solution, no solution, and infinitely many solutions graphically with three planes
- Explain one solution, no solution, and infinitely many solutions algebraically when solving a system of three variable linear equations
Linear Equations in Three Variables
A linear equation in one variable, which can be written as [latex]ax=b[/latex], can be graphed as a single point, which has no dimensions (see figure 1). A linear equation in two variables, which can be written as [latex]ax+by=c[/latex], can be graphed as a line, which has one dimension (i.e., length) (see figure 2). If we add another variable term, we get a linear equation in three variables, which can be written as [latex]ax+by+cz=d[/latex]. Following the pattern of dimensions, the graph of a linear equation in three variables must have two dimensions, length and width; the graph is a plane (see figure 3). Any solution of a linear equation in three variables is an ordered triple [latex]\left(x,y,z\right)[/latex]. For example, the equation [latex]2x-y+3z=6[/latex] has [latex](0, 0, 2),\;(1, -4, 0)[/latex], and [latex](1, 2, 2)[/latex] as three of an infinite number of solutions. Such solutions, and the plane that they make up, are plotted in three-dimensional space, with the [latex]z[/latex]-axis being perpendicular to both the [latex]x[/latex]– and [latex]y[/latex]-axes. We can think of a plane as an infinitely large, two-dimensional, flat sheet of paper.
| [latex]ax=b[/latex] | [latex]ax+by=c[/latex] |
[latex]ax+by+cz=d[/latex]
|
|---|---|---|
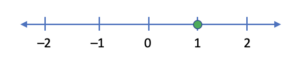 Figure 1. Solution set of [latex]ax=b[/latex] is a point. Figure 1. Solution set of [latex]ax=b[/latex] is a point. |
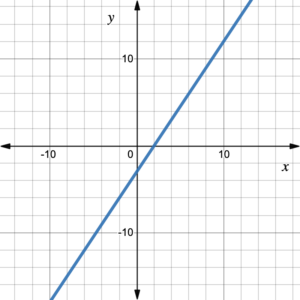
Figure 2. Solution set of [latex]ax+by=c[/latex] is a line. |
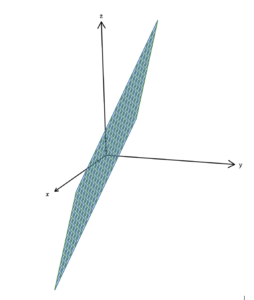
Figure 3. Solution set of [latex]ax+by+cz=d[/latex] is a plane. |
Example 1
Determine if the ordered triple is a solution of the equation [latex]2x-y+3z=8[/latex].
1. (3, –2, 0)
2. (–2, 9, 1)
Solution
To determine if the ordered triples are solutions, we must substitute the value of each variable into the equation to see if the equation is true.
|
1 |
2 |
|
[latex]\begin{aligned}2x-y+3z&=8\\2(3)-(-2)+3(0)&=8\\8&=8\;\;\;\text{True}\end{aligned}[/latex] (3, –2, 0) is a solution of the equation. |
[latex]\begin{aligned}2x-y+3z&=8\\2(-2)-(9)+3(1)&=8\\-10&=8\;\;\;\text{False}\end{aligned}[/latex] (–2, 9, 1) is not a solution of the equation. |
Try It 1
Determine if the ordered triple is a solution of the equation [latex]x-4y+2z=6[/latex].
- (3, –2, –2)
- (–2, 1, 6)
Systems of Linear Equations in Three Variables
Each equation in a system of three linear equations in three variables is represented graphically by a plane. The solution set of such a system consists of all the points where the three planes meet.
A single solution
It is possible for a system to have a single point [latex]\left(x,y,z\right)[/latex] as the solution. Graphically, the ordered triple defines the point that is the intersection of three planes in space. We can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
Solution Set, One Solution
The figure below illustrates how a system with three variables can have one solution. Systems that have a single solution are those which result in a solution set consisting of an ordered triple [latex]\left(x,y,z\right)[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
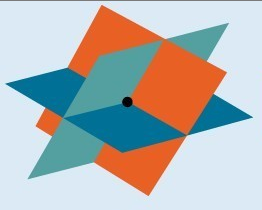
Figure 4. Three planes meeting at a single point.
For an ordered triple to be a solution for a system of three linear equations in three variables, it has to satisfy every equation in the system.
Example 2
Determine if (1, –2, 3) is a solution of the system of equations:
[latex]\begin{aligned}x+y+z&=2\\2x+y+z&=3\\x-y+2z&=5\end{aligned}[/latex]
Solution
We need to substitute the given values for each variable and see if the equation is true.
1st equation:
[latex]\begin{aligned}x+y+z&=2\\(1)+(-2)+(3)&=2\\2&=2\;\;\text{True}\end{aligned}[/latex]
2nd equation:
[latex]\begin{aligned}2x+y+z&=3\\2(1)+(-2)+(3)&=2\\3&=3\;\;\text{True}\end{aligned}[/latex]
3rd equation:
[latex]\begin{aligned}x-y+2z&=5\\(1)-(-2)+2(3)&=5\\9&=5\;\;\text{False}\end{aligned}[/latex]
(1, –2, 3) is NOT a solution of the system of equations.
Try It 2
Determine if (2, –1, 4) is a solution of the system of equations:
[latex]\begin{aligned}x+y+z&=5\\2x+y+z&=7\\x-y+2z&=11\end{aligned}[/latex]
Infinitely Many Solutions
In a system of two linear equations, we saw that it was possible to have a dependent system. This occured when the two lines representing the equations coincided resulting in an infinite number of solutions on the line. A similar thing can happen with a system of three linear equations where all three planes coincide and the solution set would be all points on the plane (figure 7). Three planes can also meet in a line (think about three consecutive pages in a book that meet at the spline), which also results in an infinite number of solutions that lie on the line where they meet (figure 5). Another option is when two identical planes intersect a third plane in a line (figure 6). Algebraically, these scenarios show up when we get an identity showing up when we are solving the system.
Infinitely Many solutions
Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space. The graphic below shows how three planes can intersect to form a line (figures 5 and 6) or a plane (figure 7) giving the system infinitely many solutions on the line or on the plane.
 Figure 5. Infinitely many solutions on the line of intersection of three planes. Figure 5. Infinitely many solutions on the line of intersection of three planes. |
|
 Figure 7. Three coincident planes. Infinite solutions on the plane. Figure 7. Three coincident planes. Infinite solutions on the plane. |
|---|
No Solution
Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a contradiction when we try to solve the system algebraically.
NO SOLUTION
Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common. Three parallel planes (figure 8), two parallel planes and one intersecting plane (figure 9), two coincident planes and a parallel plane (figure 10), and three planes that intersect the other two but not at the same location (figure 11).
| All Planes Are Parallel | Not All Planes Are Parallel |
|---|---|

Figure 8. Three parallel lines

Figure 10. Two coincident planes parallel to another plane. |

Figure 9. Two parallel planes meeting another plane. 
Figure 11. Three independent planes with no points in common. |
Example 3
A system of 3 linear equations that is being solved algebraically ends up with an equation that is an identity. Describe the two graphical scenarios that would cause this.
Solution
An identity occurs when the system is dependent. This means that either the three planes coincide, 2 of the three planes coincide, or the three planes meet in a line.
Try It 3
What can be said about a system of three linear equations in three variables when two of the equations in the system are equivalent? What does this mean graphically?
Candela Citations
- Revision and Adaptation. Authored by: Hazel McKenna. Provided by: Lumen Learning. License: CC BY: Attribution
- Learning Outcomes. Authored by: Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- Linear Equations in Three Variables. FIgures 1, 2, 3, 5, 6, 7, 8, 9 10, 11. Try It: hjm162; hjm230; hjm629.. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution

