Learning Outcomes
- Define term, like terms, and coefficient
- Define a polynomial
- Define degree of a term and degree of a polynomial
- Define leading term and leading coefficient
- Define monomials, binomials, and trinomials
Terms, Like Terms and Coefficients
In mathematics, we may see expressions such as [latex]x+5[/latex], [latex]\dfrac{4}{3}{r}^{3}[/latex], or [latex]5m-2n+6mn[/latex]. Such algebraic expressions are made up of terms.
A term is a constant, a variable, or the product or quotient of constants and one or more variables. Some examples of terms are [latex]7, \; 5y, \; 5x^2, \; -\dfrac{9a}{2b}, \; 0, \; \dfrac{4x^2}{3y}, \; \text{and}, \; t[/latex].
In the expression [latex]x+5[/latex], [latex]5[/latex] is called a constant because it does not vary and [latex]x[/latex] is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a term, or the sum of terms (remember that subtraction can always be written as a sum of the opposite).
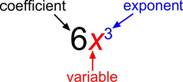
The constant that multiplies the variable(s) in a term is called the coefficient. We can think of the coefficient as the number in front of the variable. The coefficient of the term [latex]3x[/latex] is [latex]3[/latex]. When we write [latex]x[/latex], the coefficient is [latex]1[/latex], since [latex]x=1\cdot x[/latex].
Terms are called like terms if they have the same variables and corresponding exponents. All constant terms are also like terms. So among the terms [latex]5x,7,{n}^{2},4,-3x,9{n}^{2}[/latex],
- [latex]7[/latex] and [latex]4[/latex] are like terms.
- [latex]5x[/latex] and [latex]-x[/latex] are like terms.
- [latex]{n}^{2}[/latex] and [latex]9{n}^{2}[/latex] are like terms.
The number part of a term is called a coefficient. Like terms usually have different coefficients.
Example 1
1. How many terms are in the expression: [latex]6x^3y-6x+8y+3xy^2[/latex]?
2. Which of the terms are like terms: [latex]3x^3, \;\;\;7x^4, \;\;\;-2x^3, \;\;\;5x[/latex]?
3. Which of the terms are like terms: [latex]4x^2y, \;\;\;-4xy^2, \;\;\;-2xy, \;\;\;8xy^2[/latex]?
4. Why are [latex]4x^5[/latex] and [latex]4x[/latex] not like terms?
Solution
1. The expression has 4 terms: [latex]6x^3y, \;\;\;-6x, \;\;\;8y, \;\;\;3xy^2[/latex]
2. Like terms must have the same variables with the same exponents, so [latex]3x^3[/latex] and [latex]-2x^3[/latex] are like terms.
3. Like terms must have the same variables with the same exponents, so [latex]-4xy^2[/latex] and [latex]8xy^2[/latex] are like terms.
4. Like terms must have the same variables with the same exponents. [latex]4x^5[/latex] and [latex]4x[/latex] have the same variable, but different exponents so they are not like terms.
Try It 1
1. How many terms are in the expression: [latex]-6xy-x+2y+3xy^2+7[/latex]?
2. Which of the terms are like terms: [latex]2x^3, \;\;\;7x^3, \;\;\;-2x^{-3}, \;\;\;5x[/latex]?
3. Which of the terms are like terms: [latex]x^2y^3, \;\;\;-4xy^3, \;\;\;-2x^2y, \;\;\;8x^2y^2[/latex]?
4. Why are [latex]x^4y^3[/latex] and [latex]x^3y^4[/latex] not like terms?
Polynomials
A polynomial in one variable is a special algebraic expression that consists of a term or a sum (or difference) of terms in which each term is a real number, a variable, or the product of a real number and a variable with a whole number exponent.
For example, [latex]5x^2+7x-3[/latex] is a polynomial with three terms: [latex]5x^2,\;7x,\;-3[/latex]. The coefficient of [latex]x^2[/latex] is [latex]5[/latex]; the coefficient of [latex]x[/latex] is [latex]7[/latex]; and [latex]-3[/latex] is the constant term.
[latex]-\frac{4}{3}x^9+8x^4-\frac{3}{5}x^2-9[/latex] is a polynomial with four terms: [latex]-\frac{4}{3}x^9,\;8x^4,\;-\frac{3}{5}x^2,\;-9[/latex]. The coefficient of [latex]x^9[/latex] is [latex]-\frac{4}{3}[/latex]; the coefficient of [latex]x^4[/latex] is [latex]8[/latex]; the coefficient of [latex]x^2[/latex] is [latex]-\frac{3}{5}[/latex]; and the constant term is[latex]-9[/latex].
[latex]\sqrt{5}x^3[/latex] and [latex]4.563[/latex] are polynomials with just one term.
[latex]\dfrac{3}{x},\;\;x^{\frac{1}{2}},\;\;\dfrac{4}{y^2}-4x^3[/latex] are NOT polynomials because the exponents on the variables are not whole numbers. Whole number exponents exclude radicals (fractional exponents) and variables on the denominator of a fraction (negative exponents). You may not familiar with rational or negative exponents. Negative exponents will be covered in chapter 5. .
Table 1 is intended to help tell the difference between what is a polynomial and what is not.
| IS a Polynomial | Is NOT a Polynomial | Reason |
| [latex]2x^2-\frac{1}{2}x -9[/latex] | [latex]\frac{2}{x^{2}}+x[/latex] | Polynomials only have variables in the numerator |
| [latex]\frac{y}{4}-y^3[/latex] | [latex]\frac{2}{y}+4[/latex] | Polynomials only have variables in the numerator |
| [latex]\sqrt{12}\left(a\right)+9[/latex] | [latex]\sqrt{a}+7[/latex] | Roots are equivalent to rational exponents, and polynomials only have integer exponents on variables |
| Table 1. |
Monomials, Binomials, and Trinomials
The word polynomial joins two diverse roots: the Greek poly, meaning “many”, and the Latin nomen, or “name”. Consequently, polynomial means many names, which has come to be many terms. The basic building block of a polynomial is a monomial, or single term. A monomial is a single term that can be a number, a variable, or the product of a number and variable(s) with non-negative, integer exponents. A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial (two-terms). A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. Although we could continue this list with quadrinomial, quintanomial, etc., we tend to stick with the more generic polynomial after three terms.
Table 2 shows some examples of polynomials and their classification:
| [latex]5x^2-3x+4[/latex] | Trinomial; one variable | [latex]0[/latex] | Monomial; Constant | |
| [latex]5x^2y-7xy^2[/latex] | Binomial; two variables | [latex]-\dfrac{3}{4}x[/latex] | Monomial; one variable | |
| [latex]5xyz[/latex] | Monomial; three variables | [latex]x-2xy+3yz-7[/latex] | 4 terms; three variables | |
| Table 2. |
Degree of a Term and Degree of a Polynomial
The degree of a term is defined as the sum of all exponents of the variables in a term. To illustrate, the sum of the exponents in the term [latex]-5xy^2z^3[/latex] is 1+2+3=6, where 1 is the exponent of [latex]x[/latex]), 2 is the exponent of [latex]y[/latex], and 3 is the exponent of [latex]z[/latex]. A constant term is a term without any variable (e.g., 8). A constant term has degree 0 because it can be written as the number multiplied by a variable with exponent 0 (e.g., [latex]8x^0[/latex]. (Remember [latex]x^0=1[/latex], so [latex]8x^0=8\cdot 1=8[/latex].)
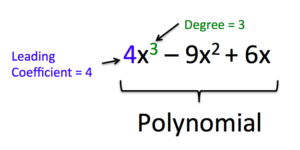
The degree of a polynomial is the highest degree of any term in the polynomial. To illustrate, there are four terms in the polynomial [latex]-\dfrac{2}{3}x^2-4xy^2z^7+2yz^3-8[/latex]. The first term has degree 2. The second term has degree 10. The third term has degree 4. The last term has degree 0. The highest degree of any term is 10. Therefore, the degree of the polynomial is 10.
When a polynomial has only one variable, the degree of the polynomial is the largest exponent on a variable. For example, the largest exponent in the polynomial [latex]4x^5-3x^7+3x^2+9-x^{12}[/latex] is 12, so the polynomial has degree 12.
Descending Order of a Polynomial
A polynomial is in descending order when the terms of the polynomial are written from the highest to the lowest term degree. For example, the polynomial [latex]-\dfrac{2}{3}x^2-4xy^2z^7+2yz^3-8[/latex] written in descending order, is [latex]-4xy^2z^7+2yz^3-\dfrac{2}{3}x^2-8[/latex]. If there are terms with the same degree, we can choose a variable (usually the one that comes first alphabetically) and use that single variable to write the terms in descending order. For example, all the terms in [latex]4x^3+2x^2y-5xy^2[/latex] have a degree of 3. This polynomial is written in descending order because, as well as being in alphabetical order, the exponent on [latex]x[/latex] decreases from term to term.
Leading Term and Leading Coefficient
The term with the highest degree is called the leading term because it is written first when the polynomial is in descending order. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the exponents on a specified variable are descending, we say that it is in standard form. It is important to note that polynomials only have non-negative, integer exponents.
Example 2
For the following polynomials, identify the degree, the leading term, and the leading coefficient. Then write the polynomial in standard form.
- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
- [latex]6xy-{x}^{3}y^2-2y^4[/latex]
- [latex]y+x+z[/latex]
Solution
- The highest power of [latex]x[/latex] is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex]. In standard form, the polynomial must be written in descending order: [latex]-4x^3+2x^2+3[/latex].
- The highest power of [latex]t[/latex] is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex]. In standard form, the polynomial must be written in descending order: [latex]5{t}^{5}-2{t}^{3}+7t[/latex].
- [latex]6xy[/latex] has degree 2; [latex]-x^3y^2[/latex] has degree 5; [latex]-2y^4[/latex] has degree 4. The highest degree of the terms is 5, so the polynomial has degree 5.
The leading term is the term containing that degree, [latex]-x^3y^2[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex]. In standard form, the polynomial must be written in descending order on the first variable: [latex]-x^3y^2+6xy-2y^4[/latex] - [latex]y[/latex], [latex]x[/latex], and [latex]z[/latex] all have degree 1, so the polynomial has degree 1. The leading term is [latex]x[/latex] due to alphabetical order, and the leading coefficient is 1. In standard form, the polynomial is [latex]x+y+z[/latex]–written in alphabetical order.
Watch the following video to see how to identify the terms, leading coefficient, and degree of a polynomial.
Try It 2
For the following polynomials, identify the degree, the leading term, and the leading coefficient. Then write the polynomial in standard form.
1. [latex]6x^4-2x^7+x^5+3x[/latex]
2. [latex]4x^3y^2-3xy-6xy^2[/latex]
3. [latex]-4x-8+9x^3y^3-3xy+7x^2y^2[/latex]
4. [latex]-\dfrac{4}{5}[/latex]
