There are many times in life where we perform one function immediately following another function. When making tea, for example, we bring cold water to a boil, then pour the boiling water over tea leaves in a teapot. The first function boils the cold water, and the second function pours the boiled water over tea leaves to make tea. The input of the first function is cold water. The output of the first function is boiled water. The input of the second function is boiled water. The output of the second function is tea. Notice that the output of the first function becomes the input of the second function i.e. boiled water. In other words, the range of the first function becomes the domain of the second function.

The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. In the example just given, the composite function is making tea.

To represent this combination of functions we use the following notation:

[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]

We read the left-hand side as, “[latex]f[/latex] composed with [latex]g[/latex] at [latex]x[/latex]“, and the right-hand side as “[latex]f[/latex] of [latex]g[/latex] of [latex]x[/latex]“. The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ[/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition of functions takes two (or more) functions and forms a new function, much as addition or multiplication takes two functions and gives a new function. However, it is important not to confuse function composition with multiplication because, in most cases [latex]f\left(g\left(x\right)\right)\ne f\left(x\right)\cdot g\left(x\right)[/latex].

It is important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the composition[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex], the function [latex]g[/latex] takes the input [latex]x[/latex] first and yields an output [latex]g\left(x\right)[/latex]. Then the function [latex]f[/latex] takes [latex]g\left(x\right)[/latex] as an input and yields an output [latex]f\left(g\left(x\right)\right)[/latex] (see figure 1).

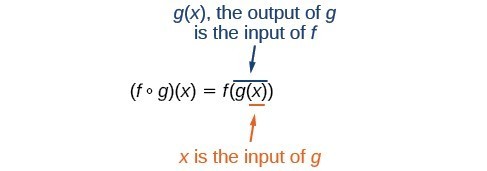
Figure 1. The composition of functions

These two examples show that the composition of functions is not commutative since [latex](f\circ g)(x)\ne (g\circ f)(x)[/latex].

Evaluating a Composite Function

There are two ways to evaluate a composite function. One way is to first find the composite function, then find the function value.

Another way to evaluate a composite function is to substitute a value for the independent variable right into the function equation of the composite function, e.g. [latex]f\left (g(2)\right )[/latex].