Learning Objectives
- Explain the inverse of a function
- Evaluate the inverse of polynomial function
- Graph the inverse of a polynomial function
- by switching domain and range
- using the line of symmetry [latex]y=x[/latex]
- Determine whether the inverse of a polynomial function is a function
- by mapping
- by determining if the original function is one-to-one
- by the vertical line test
- Find the equation of an inverse function
The Inverse of a Function
We explored the concept of inverse functions in section 1.3 where we defined the inverse of a function as the switch between the domain and range of the function (or mapping). It is the exchange of the input and output of a function. We discovered that while all functions have inverses, only one-to-one-functions have inverses that are also functions. The notation for the inverse of a one-to-one function [latex]f[/latex] is [latex]f^{-1}[/latex], which is read “the inverse of [latex]f[/latex]. Recall that the symbol “[latex]-1[/latex]” is not an exponent; it means “the inverse”. Therefore, the notation [latex]f^{-1}[/latex] means the inverse of the function [latex]f[/latex].
For example, if a function is defined as the set of ordered pairs
[latex]f:\;\{(1, 2), (3, 8), (4, 2)\}[/latex],
it has an inverse
[latex]\{(2, 1), (8, 3), (2, 4)\}[/latex].
However, this inverse is NOT a function because the input 2 has two outputs, 1 and 4. This is because the original function [latex]f[/latex] was NOT a one-to-one function (the function value 2 is the output of two domain values 1 and 4).
On the other hand, if a one-to-one function is defined as the set of ordered pairs
[latex]g:\;\{(1, 2), (3, 8), (4, 9)\}[/latex],
then its inverse function is
[latex]g^{-1}:\; \{(2, 1), (8, 3), (9, 4)\}[/latex],
which is a function. Consequently, we can use the inverse function notation [latex]g^{-1}[/latex], which we could not use with the inverse of [latex]f[/latex].
Inverse of a function
Every function has an inverse, but only a one-to-one function has an inverse function.
To evaluate the inverse of a one-to-one function, we need to switch the input and output of the function. The output of the original function becomes the input of its inverse function, and the input of the original function becomes the output of its inverse function. To illustrate,
[latex]f(1)=2[/latex], means [latex]f^{-1}(2)=1[/latex]
[latex]f(3)=8[/latex], means [latex]f^{-1}(8)=3[/latex]
[latex]f(4)=9[/latex], means [latex]f^{-1}(9)=4[/latex]
Example 1
For the function [latex]f(x)=3x+5[/latex], find:
- [latex]f^{-1}(17)[/latex]
- [latex]f^{-1}(-1)[/latex]
- [latex]f^{-1}(0)[/latex]
Solution
1. 17 is the input of the inverse function so this means that 17 was the output of the original function. To find [latex]f^{-1}(17)[/latex] we need to find the associated [latex]x[/latex]-value when [latex]f(x)=17[/latex].
[latex]\begin{aligned}f(x)&=3x+5\\17&=3x+5\\12&=3x\\4&=x\end{aligned}[/latex]
So, since [latex]f(4)=17[/latex], [latex]f^{-1}(17)=4[/latex].
2. –1 is the input of the inverse function so this means that –1 was the output of the original function. To find [latex]f^{-1}(–1)[/latex] we need to find the associated [latex]x[/latex]-value when [latex]f(x)=-1[/latex].
[latex]\begin{aligned}f(x)&=3x+5\\-1&=3x+5\\-6&=3x\\-2&=x\end{aligned}[/latex]
So, since [latex]f(-2)=-1[/latex], [latex]f^{-1}(-1)=-2[/latex].
3. 0 is the input of the inverse function so this means that 0 was the output of the original function. To find [latex]f^{-1}(0)[/latex] we need to find the associated [latex]x[/latex]-value when [latex]f(x)=0[/latex].
[latex]\begin{aligned}f(x)&=3x+5\\0&=3x+5\\-5&=3x\\-\dfrac{5}{3}&=x\end{aligned}[/latex]
So, since [latex]f(-\dfrac{5}{3})=0[/latex], [latex]f^{-1}(0)=-\dfrac{5}{3}[/latex].
Try It 1
For the function [latex]f(x)=-2x+7[/latex], find:
- [latex]f^{-1}(5)[/latex]
- [latex]f^{-1}(-3)[/latex]
- [latex]f^{-1}(0)[/latex]
Graphing the Inverse of a Polynomial Function
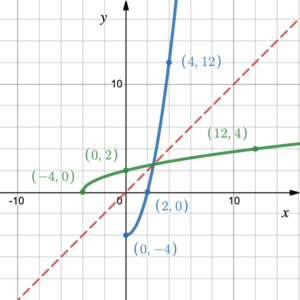
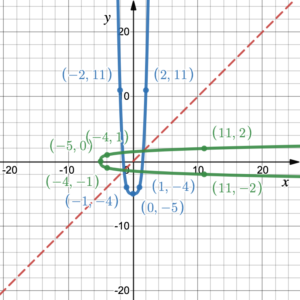
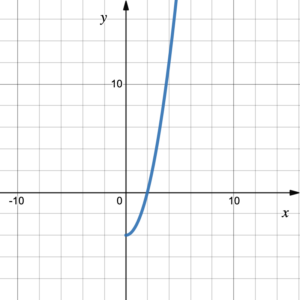
If we are given the graph of a polynomial function on the coordinate plane we can graph its inverse by switching the [latex]x[/latex] and [latex]y[/latex] coordinates for every point on the graph. Figure 1 shows that if we switch the coordinates of the points on the blue graph (–2, –4), (0, 4) and (2, 12) to (–4, –2), (4, 0), and (12, 2) we get the green graph, which is the inverse of the blue graph.
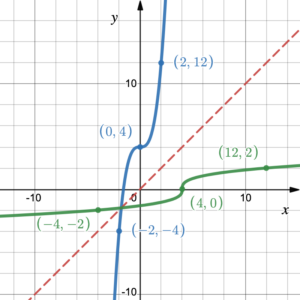
Figure 1. Graphing an inverse function
Another way to graph the inverse is to reflect the graph across the line [latex]y = x[/latex]. Figure 1 also shows that the blue curve and its inverse the green curve are reflections of one another across the line of symmetry [latex]y = x[/latex]. The green curve is the inverse of the blue curve, and the blue curve is the inverse of the green curve.
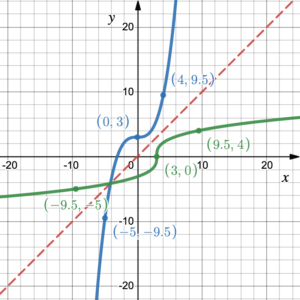
Example 2
Given the graph of the function [latex]y=f(x)[/latex], graph the inverse function [latex]y=f^{-1}(x)[/latex] using symmetry.
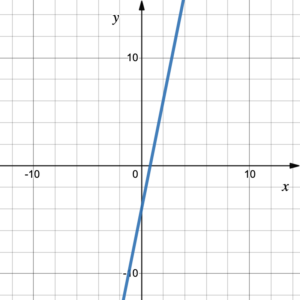
Solution
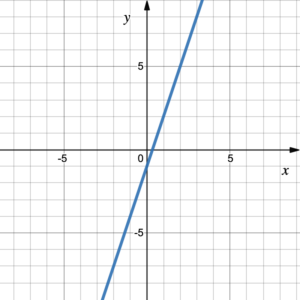
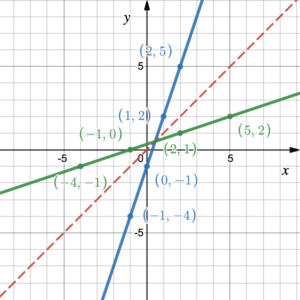
First graph the line [latex]y=x[/latex] so we can reflect the graph across this line. Choose a couple of points on the graph and switch their coordinates to help graph the reflection. (0, –4) and (2, 6) lie on the graph of the [latex]y=f(x)[/latex], so (–4, 0) and (6, 2) must lie on the graph of the inverse function [latex]y=f^{-1}(x)[/latex].
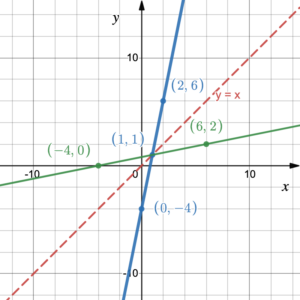
Try It 2
Given the graph of the function [latex]y=f(x)[/latex], graph the inverse function [latex]y=f^{-1}(x)[/latex] using symmetry.
It is important to note that the inverse of a function is not necessarily a function. For example, given the function [latex]f[/latex]: {(1, 2), (4, 2), (3, 6)}, its inverse is not a function. Its inverse is the set {(2, 1), (2, 4), (6, 3)}. This set is not a function because it is a one-to-many mapping (i.e., 2 is mapped to both 1 and 4). In other words, as long as there is one case of one input with many outputs in a mapping, it is not a function.
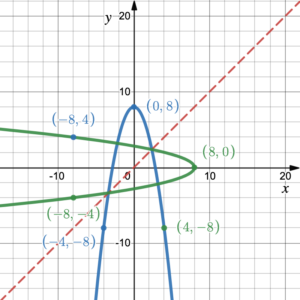
Figure 2 shows a parabola that opens up and its inverse, which opens right. The inverse is not a function because it does not pass the vertical line test. A vertical line test on the inverse graph shows that there are two intersection points with any vertical line [latex]x = c,\;c>0[/latex] and the graph of the inverse, which opens right, has one input with two outputs (a one-to-many mapping). Therefore, the inverse of the parabola is not a function.
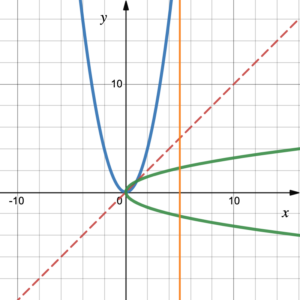
Figure 2. A parabola and its inverse
Of course, we can tell from the graph of the original function whether or not the inverse will be a function. If the original graph is NOT one-to-one, the inverse is NOT a function. As stated previously, all functions have inverses, but only one-to-one functions have inverse functions.
Example 3
Graph the inverse of the function. Determine if the inverse is a function.
| A one to one function | Not a one to one function |
|---|---|
| 1.
|
2.
|
Solution
Choose a few points on the original graph, switch the coordinates, and graph the new points. These new points will lie on the inverse. Graph the line [latex]y=x[/latex] and use the newly plotted points to help draw the reflection of the original graph across the line [latex]y=x[/latex].
| A cubic and it’s inverse | A 4th degree and it’s inverse |
|---|---|
| 1.
The original graph is one-to-one (it passes the horizontal line test), so the inverse is a function. In addition, the inverse is a function since any vertical line passes through only 1 point. |
2.
The original graph is NOT one-to-one (it fails the horizontal line test), so the inverse is NOT a function.Also, the inverse is not a function as there are vertical lines that pass through the graph at 2 points. |
Try It 3
Graph the inverse of the function. Determine if the inverse is a function.
| A linear function | A quadratic function |
|---|---|
| 1.
|
2.
|
Finding the Inverse Algebraically
To find the equation of the inverse of a polynomial function we use the same idea of switching the input and output. We start by writing [latex]y=f(x)[/latex] then switch the [latex]x[/latex] and [latex]y[/latex] variables. For the function [latex]f(x)=x^3+2[/latex], we start by writing [latex]y=x^3+2[/latex]. To find the inverse, we switch the input and the output i.e., the [latex]x[/latex] and [latex]y[/latex] variables. This results in the equation [latex]x = y^3+2[/latex], which is the equation of the inverse of the function[latex]f(x)=x^3+2[/latex]. Solving for [latex]y[/latex] we get:
[latex]\begin{aligned}x&=y^3+2\\x-2&=y^3\\ \sqrt[3]{x-2}&=y\end{aligned}[/latex]
Since [latex]f(x)=x^3+2[/latex] is a one-to-one function, its inverse is also a function. The next step is to write the inverse as a function. Because it is the inverse of the one-to-one function [latex]f[/latex], we use the notation [latex]f^{-1}[/latex] to represent it as the inverse function of [latex]f[/latex]:
[latex]f^{-1}(x) = \sqrt[3]{x - 2}[/latex]
Example 4
Find the inverse function of the polynomial function [latex]f(x)=5x-4[/latex].
Solution
Start by writing [latex]y[/latex] for [latex]f(x)[/latex]:
[latex]y=5x-4[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse equation:
[latex]x=5y-4[/latex]
Solve for [latex]y[/latex]:
[latex]\begin{aligned}x&=5y-4\\x+4&=5y\\\dfrac{x+4}{5}&=y\\ \dfrac{1}{5}x+\dfrac{4}{5}&=y\end{aligned}[/latex]
Since [latex]f(x)[/latex] is a linear function (with a non-zero slope), it is one-to-one. Write the inverse function using function notation:
[latex]\begin{aligned}y&=\dfrac{1}{5}x+\dfrac{4}{5}\\f^{-1}(x)&=\dfrac{1}{5}x+\dfrac{4}{5}\end{aligned}[/latex]
Example 5
Find the inverse function of the polynomial function [latex]g(x)=x^2+6x-1[/latex].
Solution
Start by writing [latex]y[/latex] for [latex]g(x)[/latex]:
[latex]\begin{aligned}g(x)=x^2+6x-1\\y=x^2+6x-1\end{aligned}[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse equation:
[latex]x=y^2+6y-1[/latex]
At this point we should solve for [latex]y[/latex], but we don’t know, yet, how to do that. Consequently, we leave the inverse equation as [latex]x=y^2+6y-1[/latex].
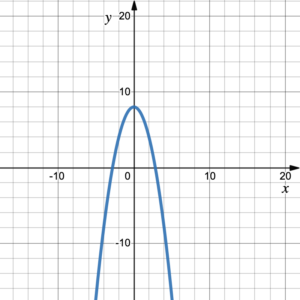
Note: Using Desmos to look at the graph of [latex]g(x)=x^2+6x-1[/latex], (figure 3), we find that [latex]g(x)[/latex] is not a one-to-one function since it does not pass the horizontal line test. Consequently, its inverse is not a function–it does not pass the vertical line test.
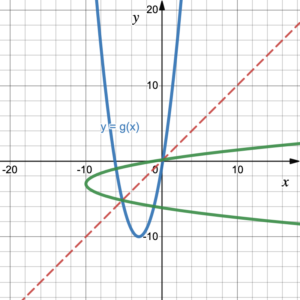
Figure 3. [latex]g(x)=x^2+6x-1[/latex] and its inverse
Try It 4
Find the inverse function of the polynomial functions:
- [latex]f(x)=x^3-4[/latex]
- [latex]g(x)=2x-6[/latex]
- [latex]h(x)=x^2-4x[/latex]
The Inverse Function of the Function [latex]f(x)=x^n+c[/latex]
Any odd polynomial function of the form [latex]f(x)=ax^n+c[/latex], where [latex]a[/latex] is a real number and [latex]n[/latex] is an odd, positive integer, is a one-to-one function. Consequently, all odd polynomial functions of the form [latex]f(x)=ax^n+c[/latex] have an inverse function. To illustrate, let’s find that inverse function for the function [latex]2x^3+4[/latex]:
[latex]\begin{aligned}f(x)&=2x^3+4&\\ y&=2x^3+4&\text{Write }y\text{ for }f(x)\\ x&=2y^3+4&\text{Switch }x\text{ and }y\\ x-4&=2y^3&\text{Solve for }y\text{: subtract }4\text{ from both sides}\\ \dfrac{1}{2}(x-4)&=y^3&\text{Divide both sides by }2\\ \sqrt[3]{\dfrac{1}{2}(x-4)}&=y&\text{Take the 3th root of both sides}\\ f^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}(x-4)}&\text{Write function notation}\end{aligned}[/latex]
Therefore, the general form of the inverse function of [latex]f(x)=ax^n+c[/latex] when [latex]n[/latex] is odd is [latex]f^{-1}(x) = \sqrt[n]{\frac{1}{a}(x - c)}[/latex].
Example 6
Find the inverse function:
- [latex]f(x)=4x^5+7[/latex]
- [latex]g(x)=-3x^7+4[/latex]
- [latex]h(x)=2x^8+5[/latex]
Solution
You may use the method described above, which is exchanging [latex]x[/latex] and [latex]y[/latex] and then solve for [latex]y[/latex].
You may also use a formula. The inverse function of [latex]f(x)=ax^n+c[/latex] when [latex]n[/latex] is odd is [latex]f^{-1}(x) = \sqrt[n]{\frac{1}{a}(x - c)}[/latex].
Identify [latex]a[/latex], [latex]c[/latex] and [latex]n[/latex] then use the general form.
- [latex]a=4,\;c=7,\;n=5[/latex] so [latex]f^{-1}(x)=\sqrt[5]{\dfrac{1}{4}(x - 7)}[/latex]
- [latex]a=-3,\;c=4,\;n=7[/latex] so [latex]f^{-1}(x)=\sqrt[7]{-\dfrac{1}{3}(x-4)}[/latex]
- [latex]a=2,\;c=5,\;n=8[/latex]. Since [latex]n=8[/latex] is even, not odd, [latex]h(x)[/latex] does not have an inverse function.
Try It 5
Find the inverse function:
- [latex]f(x)=9x^3+5[/latex]
- [latex]g(x)=-6x^8+4[/latex]
- [latex]h(x)=2x^9-3[/latex]
Candela Citations
- Inverse and Inverse Function. Authored by: Leo Chang and Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- All Examples and Try Its. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution