Learning Outcomes
For the quadratic function [latex]f(x)=x^2[/latex],
- Perform vertical and horizontal shifts
- Perform vertical compressions and stretches
- Perform reflections across the [latex]x[/latex]-axis
- Explain the vertex form of a quadratic function
- Write the equation of a transformed quadratic function using the vertex form
- Determine the equation of a quadratic function given its vertex and a point on the graph.
Vertical Shifts
If we shift the graph of the function [latex]f(x)=x^2[/latex] up 5 units, all of the points on the graph increase their [latex]y[/latex]-coordinates by 5, but their [latex]x[/latex]-coordinates remain the same. Therefore, the equation of the function [latex]f(x)=x^2[/latex] after it has been shifted up 5 units transforms to [latex]f(x)=x^2+5[/latex]. Table 1 shows the changes to specific values of this function, which are replicated on the graph in figure 1.
| [latex]x[/latex] | [latex]x^2[/latex] | [latex]x^2+5[/latex] |

Figure 1. Shifting the graph of [latex]f(x)=x^2[/latex] up 5 units. Every point [latex](x, y)[/latex] moves to ([latex](x, y+5)[/latex]. |
|---|---|---|---|
| -3 | 9 | 14 | |
| -2 | 4 | 9 | |
| -1 | 1 | 6 | |
| 0 | 0 | 5 | |
| 1 | 1 | 6 | |
| 2 | 4 | 9 | |
| 3 | 9 | 14 | |
| Table 1. [latex]f(x)=x^2[/latex] is transformed to [latex]f(x)=x^2+5[/latex] | |||
If we shift the graph of the function [latex]f(x)=x^2[/latex] down 3 units, all of the points on the graph decrease their [latex]y[/latex]-coordinates by 3, but their [latex]x[/latex]-coordinates remain the same. Therefore, the equation of the function [latex]f(x)=x^2[/latex] after it has been shifted down 3 units transforms to [latex]f(x)=x^2-3[/latex]. Table 2 shows the changes to specific values of this function, which are replicated on the graph in figure 2.
| [latex]x[/latex] | [latex]x^2[/latex] | [latex]x^2-3[/latex] |

Figure 2. Shifting the graph of [latex]f(x)=x^2[/latex] down 3 units. Every point [latex](x, y)[/latex] moves to [latex](x, y-3)[/latex]. |
|---|---|---|---|
| -3 | 9 | 6 | |
| -2 | 4 | 1 | |
| -1 | 1 | -2 | |
| 0 | 0 | -3 | |
| 1 | 1 | -2 | |
| 2 | 4 | 1 | |
| 3 | 9 | 6 | |
| Table 2. [latex]f(x)=x^2[/latex] is transformed to [latex]f(x)=x^2-3[/latex] | |||
Vertical shifts
We can represent a vertical shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]k[/latex], to the function:
[latex]f(x)=x^2 + k[/latex]
If [latex]k>0[/latex], the graph shifts upwards and if [latex]k<0[/latex] the graph shifts downwards.
Change the value of [latex]k[/latex] in the interactive desmos graph in figure 3 by moving the vertex up or down.
Figure 3. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=x^2+k[/latex]
Every point [latex](x, y)[/latex] moves to [latex](x, y+k)[/latex].
Example 1
If the function [latex]f(x)=x^2[/latex] is shifted down 7 units, what is the equation of the transformed function?
Solution
When a function is shifted down by 7 units, all of the function values are decreased by 7.
[latex]f(x)=x^2[/latex] is transformed to [latex]f(x)=x^2-7[/latex]
Try It 1
If the function [latex]f(x)=x^2[/latex] is shifted up 4 units, what is the equation of the transformed function?
Horizontal Shifts
If we shift the graph of the function [latex]f(x)=x^2[/latex] right 4 units, all of the points on the graph increase their [latex]x[/latex]-coordinates by 4, but their [latex]y[/latex]-coordinates remain the same. The vertex (0, 0) in the original graph is moved to (4, 0) (figure 3). Any point [latex](x, y)[/latex] on the original graph is moved to [latex](x+4, y)[/latex].
But what happens to the original function [latex]f(x)=x^2[/latex]? An automatic assumption may be that since [latex]x[/latex] moves to [latex]x+4[/latex] that the function will become [latex]f(x)=(x+4)^2[/latex]. But that is NOT the case. Remember that the new vertex is (4, 0) and if we substitute [latex]x=4[/latex] into the function [latex]f(x)=(x+4)^2[/latex] we get [latex]f(4)=(4+4)^2=64\ne0[/latex]!! The way to get a function value of zero is for the transformed function to be [latex]f(x)=(x-4)^2[/latex]. Then [latex]f(4)=(4-4)^2=0[/latex]. So the function [latex]f(x)=x^2[/latex] transforms to [latex]f(x)=(x-4)^2[/latex] after being shifted 4 units to the right. The reason is that when we move the function 4 units to the right, the [latex]x[/latex]-value increases by 4 and to keep the corresponding [latex]y[/latex]-coordinate the same in the transformed function, the [latex]x[/latex]-coordinate of the transformed function needs to subtract 4 to get back to the original [latex]x[/latex] that is associated with the original [latex]y[/latex]-value. Table 3 shows the changes to specific values of this function, and the graph is shown in figure 4.
| [latex]x[/latex] | [latex]x-4[/latex] | [latex](x-4)^2[/latex] |

Figure 4. Shift the graph right 4 units. |
|---|---|---|---|
| 1 | -3 | 9 | |
| 2 | -2 | 4 | |
| 3 | -1 | 1 | |
| 4 | 0 | 0 | |
| 5 | 1 | 1 | |
| 6 | 2 | 4 | |
| 7 | 3 | 9 | |
| Table 3. Shifting the graph right by 4 units transforms [latex]f(x)=x^2[/latex] into [latex]f(x)=(x-4)^2[/latex] | |||
On the other hand, if we shift the graph of the function [latex]f(x)=x^2[/latex] left by 7 units, all of the points on the graph decrease their [latex]x[/latex]-coordinates by 7, but their [latex]y[/latex]-coordinates remain the same. So any point [latex](x, y)[/latex] on the original graph moves to [latex](x-7, y[/latex]. Consequently, to keep the same [latex]y[/latex]-values we need to increase the [latex]x[/latex]-value by 7 in the transformed function. The equation of the function after being shifted left 7 units is [latex]f(x)=(x+7)^2[/latex]. Table 4 shows the changes to specific values of this function, and the graph is shown in figure 5.
| [latex]x[/latex] | [latex]x+7[/latex] | [latex](x+7)^2[/latex] |

Figure 5. Shifting [latex]f(x)=x^2[/latex] left by 7 units to get [latex]f(x)=(x+7)^2[/latex] |
|---|---|---|---|
| -10 | -3 | 9 | |
| -9 | -2 | 4 | |
| -8 | -1 | 1 | |
| -7 | 0 | 0 | |
| -6 | 1 | 1 | |
| -5 | 2 | 4 | |
| -4 | 3 | 9 | |
| Table 4. Shifting the graph left by 7 units transforms [latex]f(x)=x^2[/latex] into [latex]f(x)=(x+7)^2[/latex] | |||
horizontal shifts
We can represent a horizontal shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]h[/latex], to the variable [latex]x[/latex], before squaring.
[latex]f(x)=(x-h)^2[/latex]
If [latex]h>0[/latex] the graph shifts toward the right and if [latex]h<0[/latex] the graph shifts to the left.
Change the value of [latex]h[/latex] in the interactive desmos graph in figure 6 by moving the vertex left or right.
Figure 6. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=(x-h)^2[/latex]
tip for success
Remember that the negative sign inside the argument of the vertex form of a parabola (in the parentheses with the variable [latex]x[/latex] ) is part of the formula [latex]f(x)=(x-h)^2 +k[/latex].
If [latex]h>0[/latex], we have [latex]f(x)=(x-h)^2+k=(x-\text{positive number})^2 +k[/latex]. You’ll see the negative sign, but the graph will shift right.
If [latex]h<0[/latex], we have [latex]f(x)=(x-h)^2+k=(x-\text{negative number})^2 +k \rightarrow f(x)=(x+\text{positive number})^2+k[/latex], since subtracting a negative number is equivalent to adding a positive number. You’ll see the positive sign, but the graph will shift left.
Example 2
If the function [latex]f(x)=x^2[/latex] is shifted left by 5 units, what is the equation of the transformed function?
Solution
When a function is shifted left by 5 units, all of the [latex]x[/latex]-values are decreased by 5. So we have to add 5 to the [latex]x[/latex]-values in the transformed function to keep the correct function values.
[latex]f(x)=x^2[/latex] is transformed to [latex]f(x)=(x+5)^2[/latex]
Try It 2
If the function [latex]f(x)=x^2[/latex] is shifted right by 8 units, what is the equation of the transformed function?
Stretching Up and Compressing Down
If we vertically stretch the graph of the function [latex]f(x)=x^2[/latex] by a factor of 2, all of the [latex]y[/latex]-coordinates of the points on the graph are multiplied by 2, but their [latex]x[/latex]-coordinates remain the same. Since the vertex of [latex]f(x)=x^2[/latex] is (0, 0), it transforms to (0, 0). That is, [latex]2\times0^2=2\times0=0[/latex]. The vertex, since it is an [latex]x[/latex]-intercept, stays at the same location (0, 0). In other words, the vertex is the anchor point in the stretching process. The equation of the function after the graph is stretched by a factor of 2 is [latex]f(x)=2x^2[/latex]. The reason for multiplying [latex]x^2[/latex] by 2 is that each [latex]y[/latex]-coordinate is doubled, and since[latex]y=x^2[/latex], [latex]x^2[/latex] is doubled. Table 5 shows this change and the graph is shown in figure 7.
| [latex]x[/latex] | [latex]x^2[/latex] | [latex]2x^2[/latex] |

Figure 7. [latex]f(x)=x^2[/latex] transformed to [latex]f(x)=2x^2[/latex]. Each [latex]y[/latex]-value is doubled. |
|---|---|---|---|
| -3 | 9 | 18 | |
| -2 | 4 | 8 | |
| -1 | 1 | 2 | |
| 0 | 0 | 0 | |
| 1 | 1 | 2 | |
| 2 | 4 | 8 | |
| 3 | 9 | 18 | |
| Table 5. Stretching the graph vertically by a factor of 2 transforms [latex]f(x)=x^2[/latex] into [latex]f(x)=2x^2[/latex] | |||
On the other hand, if our factor is [latex]\dfrac{1}{2}[/latex] and we vertically compress the graph of the function [latex]f(x)=x^2[/latex] all of the [latex]y[/latex]-coordinates of the points on the graph are halved, but their [latex]x[/latex]-coordinates remain the same. This means the [latex]y[/latex]-coordinates are multiplied by [latex]\dfrac{1}{2}[/latex], or divided by 2. The [latex]x[/latex]-intercept (0, 0) of [latex]f(x)=x^2[/latex] is the only point that doesn’t move. In other words, the [latex]x[/latex]-intercept is the anchor point in the compressing process. The equation of the function after being compressed is [latex]f(x)=\dfrac{1}{2}x^2[/latex]. The reason for multiplying [latex]x^2[/latex] by [latex]\dfrac{1}{2}[/latex] is that each [latex]y[/latex]-coordinate becomes half of the original value when it is divided by 2. Table 6 shows this change and the graph is shown in figure 8.
| [latex]x[/latex] | [latex]x^2[/latex] | [latex]\frac{1}{2}x^2[/latex] |

Figure 8. Compressing the graph when the factor is [latex]\frac{1}{2}[/latex]. Each [latex]y[/latex]-value is divided by 2. |
|---|---|---|---|
| -3 | 9 | 4.5 | |
| -2 | 4 | 2 | |
| -1 | 1 | 0.5 | |
| 0 | 0 | 0 | |
| 1 | 1 | 0.5 | |
| 2 | 4 | 2 | |
| 3 | 9 | 4.5 | |
| Table 6. When the factor is [latex]\dfrac{1}{2}[/latex] the graph is compressed and transforms [latex]f(x)=x^2[/latex] into [latex]f(x)=\dfrac{1}{2}x^2[/latex] | |||
Change the value of [latex]a[/latex] in the interactive desmos graph in figure 9 by moving the point [latex](1, a)[/latex] vertically.
Figure 9. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=ax^2[/latex]
vertical stretching and compressing
A stretch or compression of the graph of [latex]f(x)=x^2[/latex] can be represented by multiplying the [latex]x^2[/latex] by a constant, [latex]a>0[/latex].
[latex]f(x)=ax^2[/latex]
The magnitude of [latex]a[/latex] indicates the stretch/compression of the graph. If [latex]a>1[/latex], the graph is stretched vertically by a factor of [latex]a.[/latex] If [latex]0 If the function [latex]f(x)=x^2[/latex] is compressed to one-quarter of its original height, what is the equation of the transformed function? What happens to the points (0, 0) and (1, 1) on the graph of the original function? When a function is compressed to one-quarter of its original height, [latex]a=\dfrac{1}{4}[/latex] in the transformed equation [latex]f(x)=ax^2[/latex]. So [latex]f(x)=x^2[/latex] is transformed to [latex]f(x)=\dfrac{1}{4}x^2[/latex]. The point (0, 0) stays the same and the point (1, 1) moves to [latex]\left (1,\dfrac{1}{4}\right )[/latex] since the [latex]y[/latex]-values are divided by 4. If the function [latex]f(x)=x^2[/latex] is stretched by a factor of 9, what is the equation of the transformed function? What happens to the points (0, 0) and (1, 1) on the graph of the original function? When the graph of the function [latex]f(x)=x^2[/latex] is reflected across the [latex]x[/latex]-axis, the [latex]y[/latex]-coordinates of all of the points on the graph change their signs, from positive to negative values or from negative to positive values, while the [latex]x[/latex]-coordinates remain the same. The equation of the function after [latex]f(x)=x^2[/latex] is reflected across the [latex]x[/latex]-axis is [latex]f(x)=-x^2[/latex]. The graph changes from opening upwards to opening downwards. Table 7 shows the effect of such a reflection on the functions values and the graph is shown in figure 10. Figure 10. Reflection across [latex]x[/latex]=axis. [latex](x, y)[/latex] transforms to [latex](x, -y)[/latex]. All of the transformations we have applied to the function [latex]f(x)=x^2[/latex] can be combined. The result is the function [latex]f(x)=a(x-h)^2+k[/latex], where [latex]a[/latex] represents vertical stretching ([latex]a>1[/latex]) and compression ([latex]0 The vertex form of a quadratic function is [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] where [latex]\left(h, k\right)[/latex] is the vertex, and [latex]a[/latex] represents stretching ([latex]a>1[/latex]), compression ([latex]0 If we were to multiply and simplify the vertex form of a quadratic function, the quadratic function would turn into standard form: [latex]f(x)=ax^2+bx+c[/latex], where [latex]a, b, c[/latex] are real numbers. the value of [latex]a[/latex] in standard form is the same value of [latex]a[/latex] in vertex form. Move the red dots in figure 11 to change the values of [latex]a, h[/latex], and [latex]k[/latex], and watch the transformation unfold. Figure 11. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=a(x-h)^2+k[/latex]Example 3
Solution
Try It 3
Reflection across the [latex]x[/latex]-axis
[latex]x[/latex]
[latex]x^2[/latex]
[latex]-x^2[/latex]

-3
9
-9
-2
4
-4
-1
1
-1
0
0
0
1
1
-1
2
4
-4
3
9
-9
Table 7. Reflecting the graph of [latex]f(x)=x^2[/latex] across the [latex]x[/latex]-axis transforms [latex]f(x)=x^2[/latex] into [latex]f(x)=-x^2[/latex]
Vertex Form of a Quadratic Function
VERTEX form of a quadratic equation
Example 4
The function [latex]f(x)=x^2[/latex] is transformed by shifting the graph to the right by 4 units then down by 3 units. Write the vertex form of the function that represents this transformation.
Solution
Moving the graph right by 4 units means that [latex]h=4[/latex].
Moving the graph down by 3 units means tha [latex]k=-3[/latex]
Vertex form is [latex]f(x)=a(x-h)^2+k[/latex] so the transformed function is [latex]f(x)=(x-4)^2-3[/latex].
Example 5
The function [latex]f(x)=x^2[/latex] is transformed by reflecting the graph across the [latex]x[/latex]-axis, stretching the graph by a factor of 4, shifting the graph to the left by 1 unit then up by 7 units. Write the vertex form of the function that represents this transformation.
Solution
Reflecting the graph across the [latex]x[/latex]-axis and stretching the graph by a factor of 4 means that [latex]a=-4[/latex].
Moving the graph left by 1 unit means that [latex]h=-1[/latex].
Moving the graph up by 7 units means that [latex]k=7[/latex]
Vertex form is [latex]f(x)=a(x-h)^2+k[/latex] so the transformed function is [latex]f(x)=-4(x+1)^2+7[/latex].
Try It 4
The function [latex]f(x)=x^2[/latex] is transformed by reflecting the graph across the [latex]x[/latex]-axis and shifting the graph to the left by 3 units. Write the vertex form of the function that represents this transformation.
Try It 5
The function [latex]f(x)=x^2[/latex] is transformed by compressing the graph to one-half of its original height, shifting the graph to the right by 5 units then down 4 units. Write the vertex form of the function that represents this transformation.
Determining the Equation of a Quadratic Function
The vertex form of a quadratic function is [latex]f(x)=a(x-h)^2+k[/latex], where [latex]a, h, k[/latex] are real numbers and [latex]a\ne 0[/latex]. So, if we know the values of [latex]a, h, k[/latex], we can write the corresponding function. For example, if we are told that [latex]h=2,\;k=5,\;a=3[/latex]. Then the function is [latex]f(x)=3(x-2)^2+5[/latex]. Figure 12 shows the graph.
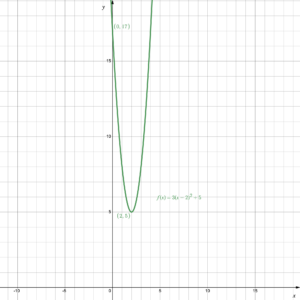
Figure 12. Graph of [latex]f(x)=3(x-2)^2+5[/latex]
What if we were told instead that the vertex is (2, 5) and the graph passes through the point (1, 8)? Can we find the equation of the function knowing this information?
Example 6
Determine the function whose graph has a vertex at (–4, 1) and that passes through the point (0, 2).
Solution
Since we know the vertex, we know [latex]h=-4,\;k=1[/latex].
Therefore, [latex]f(x)=a(x+4)^2+1[/latex].
To find [latex]a[/latex], we substitute the point (0, 2) for [latex](x, y)[/latex]:
[latex]\begin{aligned}y&=a(x+4)^2+1\\2&=a(0+4)^2+1\\2&=16a+1\\1&=16a\\\dfrac{1}{16}&=a\end{aligned}[/latex]
Consequently, [latex]f(x)=\dfrac{1}{16}\left (x+4\right )^2+1[/latex].
Try It 6
Determine the function whose graph has a vertex at (6, –2) and that passes through the point (1, –5).
Candela Citations
- Transformations of the Quadratic Function . Authored by: Leo Chang and Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Figure 3. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=x^2+b[/latex]. Authored by: Hazel McKenna. Provided by: Utah Valley University. Located at: https://www.desmos.com/calculator/k32ib1qwhr. License: CC BY: Attribution
- Figure 6. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=(x-h)^2[/latex]. Authored by: Hazel McKenna. Provided by: Utah Valley University. Located at: https://www.desmos.com/calculator/at1khozktd. License: CC BY: Attribution
- Figure 9. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=ax^2[/latex]. Authored by: Hazel McKenna. Provided by: Utah Valley University. Located at: https://www.desmos.com/calculator/jyngdxpkzl. License: CC BY: Attribution
- Figure 11. Interactive transformation from [latex]f(x)=x^2[/latex] to [latex]f(x)=a(x-h)^2+k[/latex]. Authored by: Hazel McKenna. Provided by: Utah Valley University. Located at: https://www.desmos.com/calculator/xhd1sutekk. License: CC BY: Attribution
- Determining the Equation of a Quadratic Function. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Adaptation and Revision. Authored by: Leo Chang and Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Examples 1 - 6 ; Try It: hjm387, hjm484, hjm713, hjm212, hjm992, hjm383. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
