6.2: Transformations of the Logarithmic Function

Learning Objectives

For the logarithmic function $f(x)=\log_b{x}$ ,

Perform vertical and horizontal shifts
Perform vertical compressions and stretches
Perform reflections across the $x$ -axis
Perform reflections across the $y$ -axis
Determine the transformations of the logarithmic function $f(x)=a\log_b{(x-h)}+k$
Determine the equation of a function given the transformations
Determine what happens to the vertical asymptote as transformations are made

Vertical Shifts

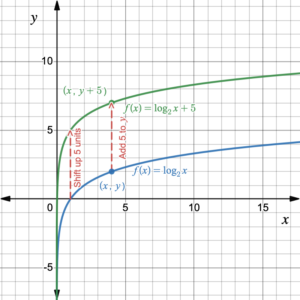
If we shift the graph of the logarithmic function $f(x)=\log_2{x}$ up 5 units, all of the points on the graph increase their $y$ -coordinates by 5, but their $x$ -coordinates remain the same. Therefore, the equation of the function $f(x)=\log_2{x}$ after it has been shifted up 5 units transforms to $f(x)=\log_2{x}+5$ . The vertical asymptote at $x=0$ remains the same. Table 1 shows the changes to specific values of this function, which are replicated on the graph in figure 1.

$x$	$\log_2{x}$	$\log_2{x}+5$	Figure 1. Shifting the graph of $f(x)=\log_2{x}$ up 5 units.
$\dfrac{1}{8}$	$-3$	$2$
$\dfrac{1}{4}$	$-2$	$3$
$\dfrac{1}{2}$	$-1$	$4$
$1$	$0$	$5$
$2$	$1$	$6$
$4$	$2$	$7$
$8$	$3$	$8$
Table 1. $f(x)=\log_2{x}$ is transformed to $f(x)=\log_2{x}+5$ .

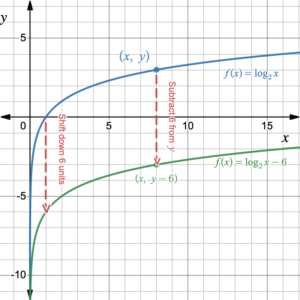
If we shift the graph of the function $f(x)=\log_2{x}$ down 6 units, all of the points on the graph decrease their $y$ -coordinates by 6, but their $x$ -coordinates remain the same. Therefore, the equation of the function $f(x)=\log_2{x}$ after it has been shifted down 6 units transforms to $f(x)=\log_2{x}-6$ .The vertical asymptote at $x=0$ remains the same. Table 2 shows the changes to specific values of this function, which are replicated on the graph in figure 2.

$x$	$\log_2{x}$	$\log_2{x}-6$	Figure 2. Shifting the graph of $f(x)=\log_2{x}$ down 6 units.
$\dfrac{1}{8}$	$-3$	$-9$
$\dfrac{1}{4}$	$-2$	$-8$
$\dfrac{1}{2}$	$-1$	$-7$
$1$	$0$	$-6$
$2$	$1$	$-5$
$4$	$2$	$-4$
$8$	$3$	$-3$
Table 2. $f(x)=\log_2{x}$ is transformed to $f(x)=\log_2{x}-6$ .

Notice that vertical shifts up or down do not change the vertical asymptote.

Move the red dots in manipulation 1 to change the values of $b$ and $k$ . Pay attention to what happens to the graph and the relationship between the value of $k$ and the transformed function.

Manipulation 1. Vertical shifts

Vertical shifts

We can represent a vertical shift of the graph of $f(x)=\log_2{x}$ by adding or subtracting a constant, $k$ , to the function:

$f(x)=\log_2{x}+k$

If $k>0$ , the graph shifts upwards and if $k<0$ the graph shifts downwards.

Example 1

If $f(x)=\log_3x$ is shifted vertically up by 7 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted vertically down by 4 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5x+9$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2x-3$ ?

Solution

With vertical shifts, the parent function $f(x)=\log_bx$ is transformed to $f(x)=\log_bx+k$ .

$k=7$ so the transformed function is $f(x)=\log_3x+7$
$k=-4$ so the transformed function is $f(x)=\log_7x-4$
$k=9$ so the transformation was a vertical shift up by 9 units.
$k=-3$ so the transformation was a vertical shift down by 3 units.

Try It 1

If $f(x)=\log_3x$ is shifted vertically up by 2 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted vertically down by 9 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5x+3$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2x-8$ ?

Show Answer

$k=2$ so the transformed function is $f(x)=\log_3x+2$
$k=-9$ so the transformed function is $f(x)=\log_7x-9$
$k=3$ so the transformation was a vertical shift up by 3 units.
$k=-8$ so the transformation was a vertical shift down by 8 units.

Horizontal Shifts

If we shift the graph of the function $f(x)=\log_2{x}$ right 8 units, all of the points on the graph increase their $x$ -coordinates by 8, but their $y$ -coordinates remain the same. The $x$ -intercept (1, 0) in the original graph is moved to (9, 0) (figure 3). The vertical asymptote at $x=0$ shifts right by 8 units to $x=8$ . Any point $(x, y)$ on the original graph is moved to $(x+8, y)$ .

But what happens to the original function $f(x)=\log_2{x}$ ? An automatic assumption may be that since $x$ moves to $x+8$ that the function will become $f(x)=\log_2{(x+8)}$ . But that is NOT the case. Remember that the $x$ -intercept is moved to (9, 0) and if we substitute $x=9$ into the function $f(x)=\log_2{(x+8)}$ we get $f(9)=\log_2{(9+8)}=4.0875 \neq 1$ !! The way to get a function value of 0 is for the transformed function to be $f(x)=\log_2{(x-8)}$ . Then $f(9)=\log_2{(9-8)}=0$ . So the function $f(x)=\log_2{x}$ transforms to $f(x)=\log_2{(x-8)}$ after being shifted 8 units to the right. The reason is that when we move the function 8 units to the right, the $x$ -value increases by 8 and to keep the corresponding $y$ -coordinate the same in the transformed function, the $x$ -coordinate of the transformed function needs to subtract 8 to get back to the original $x$ that is associated with the original $y$ -value. Table 3 shows the changes to specific values of this function, and the graph is shown in figure 3.

$x$	$x-8$	$\log_2{(x-8)}$	Figure 3. Shifting the graph right 8 units.
$\dfrac{65}{8}$	$\dfrac{1}{8}$	$-3$
$\dfrac{33}{4}$	$\dfrac{1}{4}$	$-2$
$\dfrac{17}{2}$	$\dfrac{1}{2}$	$-1$
$9$	$1$	$0$
$10$	$2$	$1$
$12$	$4$	$2$
$16$	$8$	$3$
Table 3. Shifting the graph right by 8 units transforms $f(x)=\log_2{x}$ into $f(x)=\log_2{(x-8)}$ .

Notice that the vertical asymptote also shifts from $x=0$ to $x=8$ .

On the other hand, if we shift the graph of the function $f(x)=\log_2{x}$ left by 11 units, all of the points on the graph decrease their $x$ -coordinates by 11, but their $y$ -coordinates remain the same. So any point $(x, y)$ on the original graph moves to $(x-11, y)$ . Consequently, to keep the same $y$ -values we need to increase the $x$ -value by 11 in the transformed function. The equation of the function after being shifted left 11 units is $f(x)=\log_2{(x+11)}$ . Table 4 shows the changes to specific values of this function, and the graph is shown in figure 4.

$x$	$x+11$	$f(x)=\log_2{(x+11)}$	Figure 4. Shifting the graph left 11 units.
$-\dfrac{87}{8}$	$\dfrac{1}{8}$	–3
$-\dfrac{43}{4}$	$\dfrac{1}{4}$	–2
$-\dfrac{21}{2}$	$\dfrac{1}{2}$	–1
–10	1	0
–9	2	1
–7	4	2
–3	8	3
Table 4. Shifting the graph left by 11 units transforms $f(x)=\log_2{x}$ into $f(x)=\log_2{(x+11)}$ .

Notice that the vertical asymptote also shifts from $x=0$ to $x=-11$ .

Move the red dots in manipulation 2 to change the values of $b$ and $h$ . Pay attention to what happens to the graph and the relationship between the value of $h$ and the transformed function.

Manipulation 2. Horizontal shifts

horizontal shifts

We can represent a horizontal shift of the graph of $f(x)=\log_2{x}$ by adding or subtracting a constant, $h$ , to the variable $x$ .

$f(x)=\log_2{(x}-h)$

If $h>0$ the graph shifts toward the right and if $h<0$ the graph shifts to the left. The vertical asymptote $x=0$ shifts to $x=h$ .

Example 2

If $f(x)=\log_3x$ is shifted right by 2 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted left by 9 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{(x+3)}$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2{(x-8)}$ ?

Solution

With horizontal shifts, the parent function $f(x)=\log_bx$ is transformed to $f(x)=\log_b{(x-h)}$ .

$h=2$ so the transformed function is $f(x)=\log_3{(x-2)}$
$h=-9$ so the transformed function is $f(x)=\log_7{(x+9)}$
$h=-3$ so the transformation was a horizontal shift left by 3 units.
$h=8$ so the transformation was a horizontal shift right by 8 units

Try It 2

If $f(x)=\log_3x$ is shifted right by 7 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted left by 4 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{(x-5)}$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2{(x+4)}$ ?

Show Answer

$h=7$ so the transformed function is $f(x)=\log_3{(x-7)}$
$h=-4$ so the transformed function is $f(x)=\log_7{(x+4)}$
$h=5$ so the transformation was a horizontal shift right by 5 units.
$h=-4$ so the transformation was a horizontal shift left by 4 units

We can combine vertical and horizontal shifts by transforming $f(x)=\log_b{(x-h)}+k$ .

Move the red dots in manipulation 3 to change the values of $b, \;h$ and $k$ . Pay attention to what happens to the graph and the relationship between the values of $h$ and $h$ and the transformed function.

Manipulation 3. Vertical and horizontal shifts

Example 3

If $f(x)=\log_3x$ is shifted vertically down by 3 units and right by 2 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted left by 9 units and up by 6 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{(x-2)}+7$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2{(x+5)}-4$ ?

Solution

With horizontal and vertical shifts, the parent function $f(x)=\log_bx$ is transformed to $f(x)=\log_b{(x-h)}+k$ .

$h=2,\;k=-3$ so the transformed function is $f(x)=\log_3{(x-2)}-3$
$h=-9,\;k=6$ so the transformed function is $f(x)=\log_7{(x+9)}+6$
$h=2,\;k=7$ so the transformation was a horizontal shift right by 2 units and up by 7 units.
$h=-5,\;k=-4$ so the transformation was a horizontal shift left by 5 units and down by 4 units.

Try It 3

If $f(x)=\log_3x$ is shifted down by 7 units and right by 5 units, what is the equation of the transformed function?
If $f(x)=\log_7x$ is shifted left by 4 units and up by 3 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{(x-2)}-1$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=\log_2{(x+4)}+7$ ?

Show Answer

$h=5,\;k=-7$ so the transformed function is $f(x)=\log_3{(x-5)}-7$
$h=-4,\;k=3$ so the transformed function is $f(x)=\log_7{(x+4)}+3$
$h=2,\;k=-1$ so the transformation was a horizontal shift right by 2 units and down by 1 unit.
$h=-4,\;k=7$ so the transformation was a horizontal shift left by 4 units and up by 7 units.

Vertical Stretching and Compressing

If we vertically stretch the graph of the function $f(x)=\log_2{x}$ by a factor of 2, all of the $y$ -coordinates of the points on the graph are multiplied by 2, but their $x$ -coordinates remain the same. The equation of the function after the graph is stretched up by a factor of 2 is $f(x)=2\log_2{x}$ . The reason for multiplying $\log_2{x}$ by 2 is that each $y$ -coordinate is doubled, and since $y=\log_2{x}$ , $\log_2{x}$ is doubled. Table 5 shows this change and the graph is shown in figure 5.

$x$	$\log_2{x}$	$f(x)=2\log_2{x}$	Figure 5. Stretching the graph vertically.
$\dfrac{1}{8}$	-3	-6
$\dfrac{1}{4}$	-2	-4
$\dfrac{1}{2}$	-1	-2
1	0	0
2	1	2
4	2	4
8	3	6
Table 5. Stretching the graph vertically by a factor of 2 transforms $f(x)=\log_2{x}$ into $f(x)=2\log_2{x}$ .

On the other hand, if we vertically compress the graph of the function $f(x)=\log_2{x}$ to half of its original height, we multiply the function by the factor $\dfrac{1}{2}$ . All of the $y$ -coordinates of the points on the graph are halved, but their $x$ -coordinates remain the same. This means the $y$ -coordinates are divided by 2, or multiplied by $\dfrac{1}{2}$ . The equation of the function after being compressed is $f(x)=\dfrac{1}{2}\times\log_2{x}$ . The reason for multiplying $\log_2{x}$ by $\dfrac{1}{2}$ is that each $y$ -coordinate becomes half of the original value when it is divided by 2. Table 6 shows this change and the graph is shown in figure 6.

$x$	$\log_2{x}$	$f(x)=\dfrac{1}{2}\log_2{x}$	Figure 6. Compressing the graph vertically.
$\dfrac{1}{8}$	-3	$-\dfrac{3}{2}$
$\dfrac{1}{4}$	-2	-1
$\dfrac{1}{2}$	-1	$-\dfrac{1}{2}$
1	0	0
2	1	$\dfrac{1}{2}$
4	2	1
8	3	$\dfrac{3}{2}$
Table 6. Compressing the graph vertically by a factor of $\dfrac{1}{2}$ transforms $f(x)=\log_2{x}$ into $f(x)=\dfrac{1}{2}\log_2{x}$ .

Notice that vertical stretching and compressing do not change the vertical asymptote.

Move the red dots in manipulation 4 to change the values of $b$ and $a$ . Pay attention to what happens to the graph and the relationship between the value of $a$ and the transformed function.

Manipulation 4. Vertical stretching and compressing

vertical stretching and compressing

A stretch or compression of the graph of $f(x)=\log_2{x}$ can be represented by multiplying the function by a constant, $a>0$ .

$f(x)=a\log_2{x}$

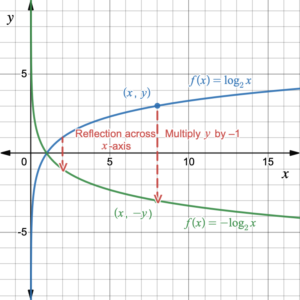
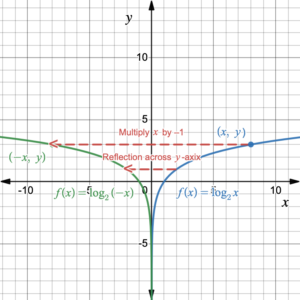
The magnitude of $a$ indicates the stretch/compression of the graph. If $a>1$ , the graph is stretched up by a factor of $a.$ If [latex]0

Example 4

If $f(x)=\log_3x$ is stretched by a factor of 7, what is the equation of the transformed function?
If $f(x)=\log_7x$ is compressed to one-third its height, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\frac{1}{6}\log_5x$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=5\log_2x$ ?

Solution

With stretching and compression, the parent function $f(x)=\log_bx$ is transformed to $f(x)=a\log_bx$ .

$a=7$ so the transformed function is $f(x)=7\log_3x$
$a=\frac{1}{3}$ so the transformed function is $f(x)=\frac{1}{3}\log_7x$
$a=\frac{1}{6}$ so the transformation was a compression to one-sixth its height
$a=5$ so the transformation was a vertical stretch by a factor of 5

Try It 4

If $f(x)=\log_3x$ is stretched by a factor of 2, what is the equation of the transformed function?
If $f(x)=\log_7x$ is compressed to one-eighth its height, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\frac{1}{4}\log_5x$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=7\log_2x$ ?

Show Answer

$a=2$ so the transformed function is $f(x)=2\log_3x$
$a=\frac{1}{8}$ so the transformed function is $f(x)=\frac{1}{8}\log_7x$
$a=\frac{1}{4}$ so the transformation was a compression to one-quarter its height
$a=7$ so the transformation was a vertical stretch by a factor of 7

Now we can combine vertical stretches and compressions with horizontal and vertical shifts.

Example 5

If $f(x)=\log_3x$ is stretched by a factor of 7, and moved down by 5 units what is the equation of the transformed function?
If $f(x)=\log_7x$ is compressed to one-third its height, moved left by 4 units and moved up by 2 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\frac{1}{5}\log_5{(x-9)}-6$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=3\log_2{(x+5)}+7$ ?

Solution

With stretching and compression, combined with shifting the parent function $f(x)=\log_bx$ is transformed to $f(x)=a\log_b{(x-h)}+k$ .

$a=7,\; k=-5$ so the transformed function is $f(x)=7\log_3x-5$
$a=\frac{1}{3},\;h=-4,\;k=2$ so the transformed function is $f(x)=\frac{1}{3}\log_7{(x+4)}+2$
$a=\frac{1}{5},\;h=9,\;k=-6$ so the transformation was a compression to one-fifth its height, a shift right by 9 units, and a shift down by 6 units
$a=3,\;-5,\;k=7$ so the transformation was a vertical stretch by a factor of 3, a shift left by 5 units, and a shift up by 7 units

Try It 5

If $f(x)=\log_3x$ is stretched by a factor of 5, and moved down by 2 units what is the equation of the transformed function?
If $f(x)=\log_7x$ is compressed to one-half its height, moved left by 7 units and moved up by 3 units, what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\frac{1}{3}\log_5{(x-2)}-3$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=9\log_2{(x+1)}+5$ ?

Show Answer

$a=5,\; k=-2$ so the transformed function is $f(x)=5\log_3x-2$
$a=\frac{1}{2},\;h=-7,\;k=3$ so the transformed function is $f(x)=\frac{1}{2}\log_7{(x+7)}+3$
$a=\frac{1}{3},\;h=2,\;k=-3$ so the transformation was a compression to one-third its height, a shift right by 2 units, and a shift down by 3 units
$a=9,\;h=-1,\;k=5$ so the transformation was a vertical stretch by a factor of 9, a shift left by 1 unit, and a shift up by 5 units

Reflections

Across the $x$ -axis

When the graph of the function $f(x)=\log_2{x}$ is reflected across the $x$ -axis, the $y$ -coordinates of all of the points on the graph change their signs, from positive to negative values or from negative to positive values, while the $x$ -coordinates remain the same. The equation of the function after $f(x)=\log_2{x}$ is reflected across the $x$ -axis is $f(x)=-\log_2{x}$ . The graph changes from increasing upwards to decreasing downwards. Table 7 shows the effect of such a reflection on the functions values and the graph is shown in figure 7.

$x$	$\log_2{x}$	$-\log_2{x}$	Figure 7. Reflecting the graph of $f(x)=\log_2{x}$ across the $x$ -axis.
$\dfrac{1}{8}$	-3	3
$\dfrac{1}{4}$	-2	2
$\dfrac{1}{2}$	-1	1
1	0	0
2	1	-1
4	2	-2
8	3	-3
Table 7. Reflecting the graph of $f(x)=\log_2{x}$ across the $x$ -axis transforms $f(x)=\log_2{x}$ into $f(x)=-\log_2{x}$ .

Notice that reflecting across the $x$ -axis does not change the vertical asymptote.

Across the $y$ -axis

When the graph of the function $f(x)=\log_2{x}$ is reflected across the $y$ -axis, the $x$ -coordinates of all of the points on the graph change their signs, from positive to negative values, while the $y$ -coordinates remain the same. The equation of the function after $f(x)=\log_2{x}$ is reflected across the $y$ -axis is $f(x)=\log_2{(-x)}$ . The graph changes from increasing from the left to decreasing from the left. Table 8 shows the effect of such a reflection on the functions values and the graph is shown in figure 8.

$x$	$-x$	$\log_2{(-x)}$	Figure 8. Reflecting the graph of $f(x)=\log_2{x}$ across the $y$ -axis.
$-\dfrac{1}{8}$	$\dfrac{1}{8}$	–3
$-\dfrac{1}{4}$	$\dfrac{1}{4}$	–2
$-\dfrac{1}{2}$	$\dfrac{1}{2}$	–1
–1	1	0
–2	2	1
–4	4	2
–8	8	3
Table 8. Reflecting the graph of $f(x)=\log_2{x}$ across the $y$ -axis transforms $f(x)=\log_2{x}$ into $f(x)=\log_2{(-x)}$

Notice that reflecting across the

$x$ -axis does not change the vertical asymptote.

Example 6

If $f(x)=\log_3x$ is reflected across the $x$ -axis what is the equation of the transformed function?
If $f(x)=\log_7x$ is reflected across the $y$ -axis what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=-\log_5{x}-6$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=-3\log_2{-x}$ ?

Solution

The $y$ -values change sign so the transformed function is $f(x)=-\log_3x$
The $x$ -values change sign so the transformed function is $f(x)=\log_7{(-x)}$
$a=-1,\;k=-6$ so the transformation was a reflection across the $x$ -axis and a shift down by 6 units
$a=-3$ and $x$ is $-x$ so the transformation was a vertical stretch by a factor of 3, a reflection across the $x$ , and a reflection across the $y$ -axis

Try It 6

If $f(x)=\log_9x$ is reflected across the $x$ -axis what is the equation of the transformed function?
If $f(x)=\log_4x$ is reflected across the $y$ -axis what is the equation of the transformed function?
What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{(-x)}+4$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=2\log_2{(-x)}$ ?

Show Answer

The $y$ -values change sign so the transformed function is $f(x)=-\log_9x$
The $x$ -values change sign so the transformed function is $f(x)=\log_4{(-x)}$
The transformation was a reflection across the $y$ -axis and a shift up by 4 units
The transformation was a vertical stretch by a factor of 2, and a reflection across the $y$ -axis

Combining Transformations

After learning all the transformations for the function $f(x)=\log_b{x}$ , we should be able to write a transformed function given specific transformations, and also determine what transformations have been performed on the function $f(x)=\log_b{x}$ , given an arbitrary transformed function $f(x)=a\log_b{(x-h)}+k$ .

Example 7

What transformations have been done to the parent function $f(x)=\log_2{x}$ to get the transformed function $f(x)=-3\log_2{(x+3)}-6$ ?

Solution

We need to identify $a,\;h,\;k$ and whether or not $x$ has a negative sign in front of it. To do this we line up the transformed function $f(x)=-3\log_2{(x+3)}-6$ with the standard function $f(x)=a\log_2{(x-h)}+k$ :

$a=-3$ means it has been stretched by a factor of 3 and reflected across the $x$ -axis.

$h=-3$ means it has been shifted left by 3 units.

$k=-6$ means it has been shifted down by 6 units.

Try It 7

What transformation was made to the parent function $f(x)=\log_5x$ if the transformed function is $f(x)=\log_5{-x}+7$ ?
What transformation was made to the parent function $f(x)=\log_2x$ if the transformed function is $f(x)=-2\log_2{(x-5)}-4$ ?

Show Answer

The transformation was a reflection across the $y$ -axis and a shift up by 7 units
The transformation was a vertical stretch by a factor of 2, a reflection across the $x$ -axis, a shift right by 5 units, and a shift down by 4 units.

Example 8

If $f(x)=\log_3x$ is reflected across the $x$ -axis, stretched by a factor of 3, and shifted left by 2 units, what is the equation of the transformed function? What happens to the vertical asymptote?
If $f(x)=\log_7x$ is reflected across the $y$ -axis, compressed to half its height, and shifted up by 7 units, what is the equation of the transformed function? What happens to the vertical asymptote?

Solution

$a=-3,\;h=-2$ so the transformed function is $-3\log_3{(x+2)}$ . The vertical asymptote is shifted left by 2 units from $x=0$ to $x=-2$ .
$a=\frac{1}{2},\;k=7$ and $x$ has a negative coefficient so the transformed function is $f(x)=\frac{1}{2}\log_7{(-x)}+7$ . Since there are no horizontal shifts, nothing happens to the vertical asymptote.

Try It 8

If $f(x)=\log_3x$ is stretched by a factor of 7, shifted right by 4 units and shifted down by 4 units, what is the equation of the transformed function? What happens to the vertical asymptote?
If $f(x)=\log_7x$ is reflected across the $x$ -axis, compressed to one-sixth its height, shifted left by 1 unit, and shifted up by 7 units, what is the equation of the transformed function? What happens to the vertical asymptote?

Show Answer

$a=7,\;h=4,\;k=-4$ so the transformed function is $f(x)=7\log_3{(x-4)}-4$ . The vertical asymptote is shifted right by 4 units from $x=0$ to $x=4$ .
$a=-\frac{1}{6},\;h=-1,\;k=7$ so the transformed function is $f(x)=-\frac{1}{6}\log_7{(x+1)}+7$ . The vertical asymptote is shifted left by 1 unit from $x=0$ to $x=-1$ .

Move the red dots in manipulation 5 to change the values of $a, h, k$ and $b$ or to reflect the graph across the $y$ -axis. Pay attention to what happens to the graph and the relationship between the values of $a,\;h,\;k$ and the transformed function.

Manipulation 5. Transformations on $f(x)=\log_b{x}$

Chapter 6: Logarithmic Functions