Learning Objectives
- Define a relation using ordered pairs, a mapping, a graph, and an equation
- Determine the domain and range of a relation
- Write the domain and range in interval notation
- Write the domain and range in set-builder notation
Parentheses, Brackets, and Braces
Parentheses ( ), brackets [ ], and braces { } play an important role in mathematics and have several different uses. Parentheses can be used to denote multiplication: [latex]3(4) = 3\cdot 4=12[/latex]. They can also be used along with brackets and braces to denote grouping and order of operations: [latex]\{3+[2-(3x-1)]\}[/latex]. Parentheses are also used to denote ordered pairs. An ordered pair consists of two numbers (or more generally two mathematical objects) enclosed by a pair of parentheses, where the order of the numbers in the pair of parentheses matters. An ordered pair has many meanings in mathematics.
Coordinates
An ordered pair may refer to the coordinates of a point on a coordinate plane. A rectangular coordinate plane (or Cartesian plane) is composed of two number lines or two axes and the plane that they form. The horizontal number line is called the [latex]x[/latex]-axis and the vertical number line is called the [latex]y[/latex]-axis. The two axes cross at a point where both the [latex]x[/latex]– and [latex]y[/latex]-values are zero, called the origin. The two axes form a grid, called a rectangular coordinate plane, and each intersection on the grid is a point (Figure 1). The points on the grid are not only integers. There are an infinite number of real number intersections that make up the grid.
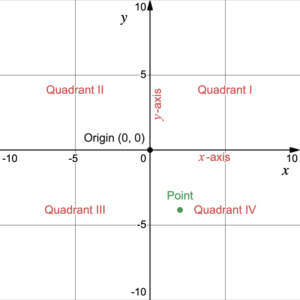
Figure 1. Rectangular coordinate plane
There are an infinite number of points on the coordinate plane. The location of a point may be specified using the values on the [latex]x[/latex] and [latex]y[/latex]-axis. The ordered pair (3, –2) refers to a point on the coordinate plane where the location is 3 relative to the horizontal number line (or [latex]x[/latex]-axis) and –2 relative to the vertical number line (or [latex]y[/latex]-axis). We call 3 the [latex]x[/latex]-coordinate and –2 the [latex]y[/latex]-coordinate. Therefore, the ordered pair [latex](3, -2)[/latex] may represent a pair of coordinates on the coordinate plane (Figure 2).

Figure 2. The point (3, –2) on the coordinate plane
Any point on the coordinate plane [latex](x, y)[/latex] is an ordered pair because it is two numbers (a pair) written in the specific order of [latex]x[/latex]-coordinate first, [latex]y[/latex]-coordinate second.
Example 1
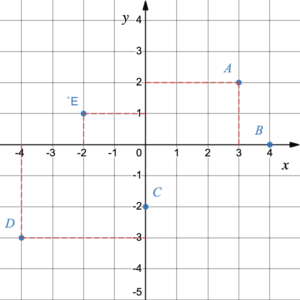
Solution
Point [latex]A[/latex] is right above [latex]3[/latex] on the [latex]x[/latex]-axis and across from [latex]2[/latex] on the [latex]y[/latex]-axis. Therefore, [latex]A=(3, 2)[/latex].
Point [latex]B[/latex] lies on [latex]4[/latex] on the [latex]x[/latex]-axis and across from [latex]0[/latex] on the [latex]y[/latex]-axis. Therefore, [latex]B=(4, 0)[/latex].
Point [latex]C[/latex] is right below [latex]0[/latex] on the [latex]x[/latex]-axis and lies on [latex]-2[/latex] on the [latex]y[/latex]-axis. Therefore, [latex]C=(0, -2)[/latex].
Point [latex]D[/latex] is right below [latex]-4[/latex] on the [latex]x[/latex]-axis and across from [latex]-3[/latex] on the [latex]y[/latex]-axis. Therefore, [latex]D=(-4, -3)[/latex].
Point [latex]E[/latex] is right above [latex]-2[/latex] on the [latex]x[/latex]-axis and across from [latex]1[/latex] on the [latex]y[/latex]-axis. Therefore, [latex]E=(-2, 1)[/latex].
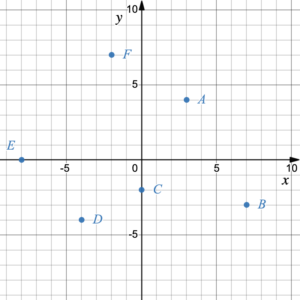
Try It 1
State the coordinates of the points on the graph:
Intervals
An ordered pair may also refer to an interval with a starting value and an ending value. The pair of numbers are ordered with the smaller number written first. For example, [latex](-1, 3)[/latex] means an interval on a number line starting at –1 and ending at 3. The parentheses means both of the two numbers –1 and 3 are not included in the interval, but are boundaries of the interval. Figure 3 shows this interval on a number line. We use an empty circle to show that an end point is not included in an interval. Since the two end points –1 and 3 are not included in the interval, they are both empty circles on the number line. Since this interval is for [latex]x[/latex], it is equivalent to the inequality [latex]1 < x < 3[/latex].
Figure 3. Interval (–1, 3)
[latex](-2, 1][/latex] represents an interval on a number line starting at –2 and ending at 1. The parentheses next to –2 tells us that –2 is not included in the interval, while the bracket next to 1 tells us that 1 is included in the interval. Figure 4 shows the interval on a number line. We use a solid circle to show that an end point is included in an interval. This interval is equivalent to [latex]-2 < x ≤ 1[/latex].
Figure 4. Interval (–2, 1]
Example 2
Write the interval.
- All values between [latex]-1[/latex] and [latex]4[/latex].
- All values between [latex]-1[/latex] and [latex]4[/latex], including [latex]4[/latex].
- All values between [latex]-1[/latex] and [latex]4[/latex], including [latex]-1[/latex] and [latex]4[/latex].
Solution
- [latex]-1[/latex] and [latex]4[/latex] are not included so we use parentheses: [latex](-1,4)[/latex]
- [latex]-1[/latex] is not included so we use parentheses on that end, and [latex]4[/latex] is included so we use a bracket on that end: [latex](-1,4][/latex]
- Both [latex]-1[/latex] and [latex]4[/latex] are included so we use brackets: [latex][-1,4][/latex]
Try It 2
Write the interval.
- All values between [latex]-7[/latex] and [latex]5[/latex].
- All values between [latex]-7[/latex] and [latex]5[/latex], including [latex]-7[/latex].
- All values between [latex]-7[/latex] and [latex]5[/latex], including [latex]-7[/latex] and [latex]5[/latex].
Example 3
Sketch the interval on a number line.
- (–3, 2)
- [4, 7]
- [latex](-\infty,0][/latex]
Solution
1. The parentheses tell us that neither –3 nor 2 are included in the interval, so we use open circles on both ends:
![]()
2. The brackets tell us that 4 and 7 are included in the interval, so we use closed circles on both ends:
![]()
3. Negative infinity can never be reached so it has a parenthesis to show that it is not included in the interval. We will use an arrow on that end of the line to show that it goes on forever. The bracket next to 0 tells us that 0 is included in the interval, so we will use a closed circle on that end:

Try It 3
Write the interval shown on the number line.
1.

2. ![]()
3. ![]()
Input – Output
An ordered pair may also refer to a relation or mapping where the first object in the pair is a source or input in a mapping and the second object in the pair is a target or output in a mapping. For example, we may define the relation double the input value to get the output value using the ordered pair idea where the second number is double the first number. Therefore, [latex](1, 2), (2, 4), (3, 6)...[/latex] are specific examples of the relation. In general, the relation is [latex](x, 2x)[/latex]. We will explore this further under Relations.
Sets
Braces { } are used when we talk about sets. A set is simply a group or collection of objects. We use braces { } to enclose the group of objects. Each object in a set is called an element. For example, {blue, red, yellow} is the set of primary colors. Blue, red, and yellow are the elements of the set. The set {2, 4, 6, 8, …} is the set of even whole numbers. The set {(1, 2), (3, 8), (4, 9)} is a set of three ordered pairs. A set that contains no elements, [latex]\{\;\}[/latex], is called the empty set and is notated [latex]\varnothing[/latex]. We will look further at sets in set builder notation.
Example 4
- Write the set of all integers between –2 and 5.
- How many elements are in the set of currently printed US currency notes?
Solution
- The integers between –2 and 5 are {–1, 0, 1, 2, 3, 4}.
- The set of currently printed US currency notes is {$1, $5, $10, $20, $50, $100} so there are 6 elements in this set.
Try It 4
- Write the set of US currency coins intended for circulation.
- How many elements are in the set of proper fractions between 0 and 1?
Relations
A relation is a way in which two or more objects are connected. For example, every person has a date of birth, so there is a relation between the person and their date of birth. Indeed, there is a relation between the set of all people and the set of all birth dates. Every perfect square has a whole number square root, so there is a relation between a perfect square and its whole number square root. Further, there is a relation between the set of perfect squares and the set of whole number square roots.
Mathematically, a binary relation is defined as a connection between two sets of objects. That relation can be represented in multiple ways: a set of ordered pairs; a mapping; a graph; or an equation.
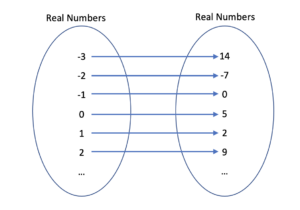
For example, the relation between two whole numbers where the second number is double the first number, may be represented in different ways:
- A set of ordered pairs shows the first number followed by the second number, or the source followed by the target: {(0, 0), (1, 2), (2, 4), (3, 6), (4, 8),…}. The ellipses … show that the established pattern continues forever.
- A mapping shows the association of the first numbers (the set of whole numbers) with an arrow that points to the corresponding second number (double the first number):

- A graph shows the set of ordered pairs plotted on the rectangular (Cartesian) coordinate plane. If the first number is represented by [latex]x[/latex] and the second number by [latex]y[/latex], the graph shows the plotted points [latex](x, y)[/latex]. Obviously, the graph does not show all possible coordinate pairs as the whole numbers start at zero and go to infinity. Notice also, that the plotted pairs are not joined by a line, as the line that joins them represents real numbers, not whole numbers.
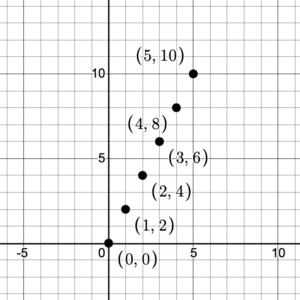
- An equation: If the first number is represented by [latex]x[/latex] and the second number by [latex]y[/latex], then since [latex]y[/latex] is double the value of [latex]x[/latex], the relation can be represented by the equation [latex]y = 2x[/latex] where [latex]x[/latex] is a whole number.
Example 5
The relation given by the set of ordered pairs {(Juan, Brown), (Ian, Blue), (Bailey, Brown), (Kirsty, Hazel), (Jean, Grey), (Freddy, Blue)} is the eye color of each named person. Create a mapping to show this relation.
Solution
We start by listing the elements of each set inside a border, then draw arrows from the person to their respective eye color.
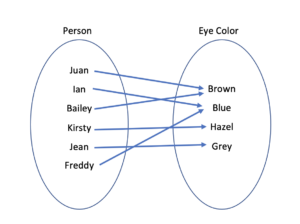
Notice that there are more people than colors, since some people share the same eye color.
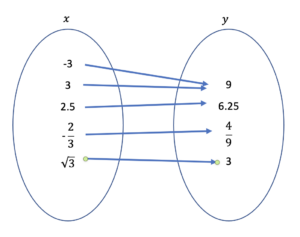
Try It 5
What relation is shown in the mapping?
Example 6
Graph the relation [latex]y=-x+3[/latex]
Solution
This relation is given in the form of a linear equation. To graph an equation we can use a table of values. Choose any [latex]x[/latex]-value and find the corresponding [latex]y[/latex]-value, then plot the ordered pairs.
| [latex]x[/latex] | [latex]y=-x+3[/latex] |
|---|---|
| -2 | [latex]y=-(-2)+3=5[/latex] |
| -1 | [latex]y=-(-1)+3=4[/latex] |
| 0 | [latex]y=-(0)+3=3[/latex] |
| 1 | [latex]y=-(1)+3=2[/latex] |
| 2 | [latex]y=-(2)+3=1[/latex] |
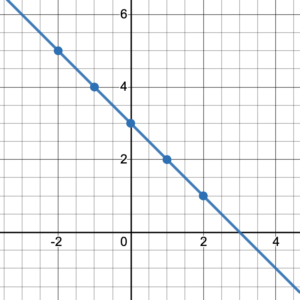
The equation [latex]y=-x+3[/latex] had no limitations on the values of [latex]x[/latex] so we can assume that it includes all real numbers. This means that we can join the dots to form a line that continues forever in both directions.
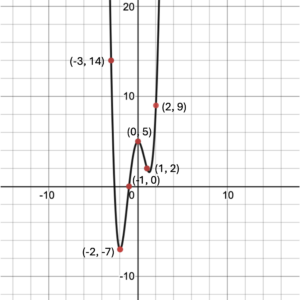
Try It 6
Use the graph to create a mapping from the set of real numbers to the set of real numbers.
Domain and Range
The word domain is used to refer to the set of elements of the source in a relation. The word range is used to refer to the set of elements of the target in a relation. For example, the domain in the relation between two whole numbers where the second number is double the first number is the set {0, 1, 2, 3, 4….}. The range in this relation is the set {0, 2, 4, 6, 8,…}.
When the relation is given as a set of ordered pairs, where the first element in the pair is mapped to the second element in the pair, the first element in the pair belongs to the domain, while the second element belongs to the range. For example, the pair (3, 5) means the element 3 in the domain is mapped to the element 5 in the range. For the set of ordered pairs {(1, 2), (4, 8), (5, -3), (4, 6)}, the domain is the set {1, 4, 5}, while the range is the set {2, 8, -3, 6}.
Try It 7
State the domain and the range of the relation {(-3, 2), (0, 3), (4, 2), (-3, 0)}.
Every graph on a coordinate plane is composed of points which are ordered pairs. Therefore, the domain of the graph will be the set of the [latex]x[/latex]-coordinates of all the points on the graph and the range will be the set of the [latex]y[/latex]-coordinates of all the points on the graph. However, depending on the graph, it may be impossible to list all the [latex]x[/latex]-coordinates for the domain and all the [latex]y[/latex]-coordinates for the range (see figure 1). In these situations, there are alternative ways to help us describe the domain and range.
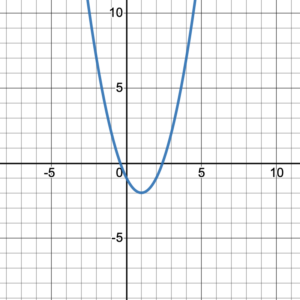
Figure 1.
Interval Notation:
Since the domain of a graph is a set of [latex]x[/latex]-values, we describe the domain of a graph using an interval. Basically, the interval describes the coverage of the graph along a number line. The covered area of the [latex]x[/latex]-coordinates of the graph in figure 1 is from negative infinity to positive infinity. Therefore, the domain is
[latex](-\infty, +\infty)[/latex]
We can do the same with the [latex]y[/latex]-coordinates of the graph to get the range. The covered area of the [latex]y[/latex]-coordinates is from the lowest value of [latex]y[/latex] where the graph turns at –2 to positive infinity. Therefore, the range is
[latex][-2,+\infty)[/latex]
In interval notation a parenthesis ( or ) means the number next to it is not included. On the other hand, a bracket [ or ] means the number next to it is included.
Try It 8
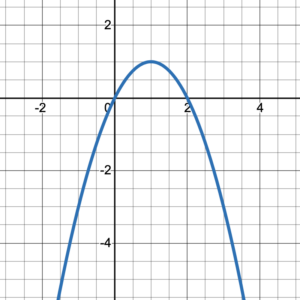
Write the domain and range of the graphed relation in interval notation:
Try It 9
Write the domain and range of the graphed relation, in interval notation:

Set-Builder Notation:
Another way to describe the domain and range is using set-builder notation. Set-builder notation specifies a set as a selection from a larger set, determined by a condition on the elements. Set-builder notation is composed of three elements, the braces (curly brackets), the variable being described, and the conditions on the variable. For example, { [latex]x[/latex] | [latex]x\in\mathbb{R}\text{ and }x > 3[/latex] }. The braces enclose elements of a set. The vertical bar is read, “such that” and the condition on the variable is placed after the vertical bar. It describes and constrains the elements of the set. [latex]x\in\mathbb{R}\text{ and }x > 3[/latex] tells us that the elements of the set are real numbers greater than 3.
The set-builder notation for the domain of the graph in figure 1 is { [latex]x\; | \;\;x\in\mathbb{R}[/latex]}. The statement [latex]x\in\mathbb{R}[/latex] is read [latex]x[/latex] is a real number and is identical to all elements on the [latex]x[/latex]-axis from negative infinity to positive infinity. The set notation for the range will be [latex]\{y\; |\;\;y\in\mathbb{R}\text{ and }y ≥ -2 \}[/latex].
Try It 10
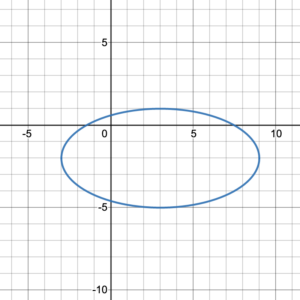
Write the domain and range of the graphed relation in set-builder notation:

Try It 11
Write the domain and range of the graphed relation in set-builder notation:
Candela Citations
- Relations and Functions. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- All Examples and Try Its. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution