Learning Objectives
- Define a function
- Determine if a relation is a function
- Determine if a function is one-to-one
- Write a function using function notation
- Determine an inverse function from a mapping or set of ordered pairs
- Determine the domain of an inverse function given the domain and range of a one-to-one function.
- Write an inverse function using function notation
Definition of a Function
A function is defined as a one-to-one or many-to-one mapping. One-to-many and many-to-many mappings are not functions. A one-to-one mapping means every element in the domain is mapped to exactly one element in the range, and every element in the range is mapped by only one element in the domain (See Figure 2). A many-to-one mapping means in addition to one-to-one, there are elements in the domain that are mapped to the same element in the range (See Figure 3).
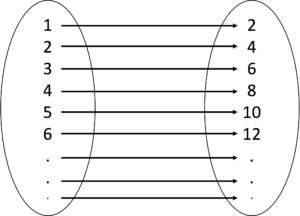
Figure 2: A one-to-one mapping is a function
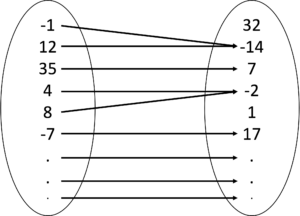
Figure 3: A many-to-one mapping is a function
This means that for a relation to be a function, every element in the domain has exactly one mapping arrow coming from it. And, for a function to be one-to-one, every element in the range has only one mapping arrow coming to it.
One-to-many and many-to-many mappings are not functions. A one-to-many mapping means, there is at least one element in the domain that is mapped to two or more elements in the range (See Figure 4). A many-to-many mapping means there are many-to-one and one-to-many cases in the mapping (See Figure 5).
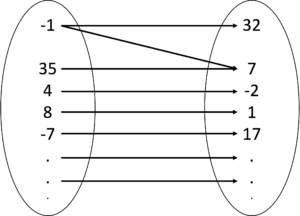
Figure 4: A one-to many mapping is NOT a function
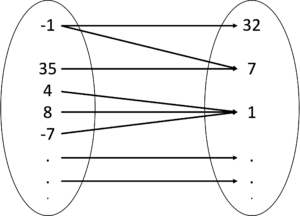
Figure 5: A many-to-many mapping is NOT a function
Relations are NOT functions if there are more than one mapping arrows coming from a least one element in the domain.
For example, the relation given by the set of ordered pairs {(1, 2), (4, 8), (5, -3), (4, 6)}, it is not a function because it is a one-to-many mapping. The element 4 in the domain is mapped to 6 and 8 in the range. In order for a relation to be a function, every element in the domain must map to only one element in the range.
Try It 1
Determine if the relations are functions:
- {(0, 6), (1, 7), (2, 9), (4, 6)}
- {(-6, 9), (7, 3), (-8, 5), (5, 4)}
- {(-8, 4), (7, 9), (-8, 6), (0, 5)}
Definition of a function
- For each value in the domain, there is one and only one corresponding value in the range.
- Every element in the domain must be mapped to one and only one corresponding element in the range.
Inverse Functions
When a function is one-to-one, it has an inverse function. An inverse function maps the range elements back to the original domain elements. The function must be one-to-one so that every range element has only one domain element to go back to. This ensures that the inverse relation is a function.
Consider the function that maps people to their social security number. That is a one-to-one function because every person has a unique social security number. The inverse function takes any given social security number and maps it back to the person it belongs to. The original function takes the domain elements of given people and maps to their unique social security number in the range. The inverse function takes its domain elements of social security number and maps it to the person that it belongs to in the functions range. So the domain of the inverse function is the range of the original function. And the range of the inverse function is the domain of the original function.

Example 1
State the inverse function of [latex]\{ (2, 1), (3, 4), (4, 7), (5, 9)\}[/latex].
Solution
First we have to check that this function is one-to-one. It is because every [latex]x[/latex]-value maps to only one [latex]y[/latex]-value and every [latex]y[/latex]-value is mapped from only one [latex]x[/latex]-value.
The domain of the inverse function is the range of the original function, and vice versa. This means that we just need to switch the [latex]x[/latex]-values and [latex]y[/latex]-values.
Inverse function = [latex]\{ (1, 2), (4, 3), (7, 4), (9, 5)\}[/latex].
Try It 2
State the inverse function, if it exists:
- Original function = [latex]\{ (1, 2), (2, 3), (3, 4), (4, 5), (5, 6)\}[/latex]
- Original function = [latex]\{ (1, 2), (2, 3), (3, 2), (4, 3)\}[/latex]
Try It 3
If a one-to-one function has a domain of [latex](-\infty, +\infty)[/latex] and a range of [latex](-\infty, 6)[/latex], state the domain and range of the inverse function.
Example 2
If [latex]f[/latex] is a function that says. “add 3 to any real number”,
- Create a mapping, using at least four numbers and a variable, that describes the function [latex]f[/latex].
- Create a mapping, using at least four numbers and a variable, that describes the inverse function of [latex]f[/latex].
- Describe the inverse function of [latex]f[/latex] in words.
Solution
Choose any four real numbers for the domain of the function [latex]f[/latex], then add 3 to map them to the range. For a variable domain element [latex]x[/latex], the mapping is [latex]x+3[/latex]. For the inverse function, the domain of the original function becomes the range of the inverse function and vice versa. For a variable domain element [latex]x[/latex], the mapping for the inverse function is [latex]x-3[/latex].
For the inverse function, the domain of the original function becomes the range of the inverse function and vice versa. For a variable domain element [latex]x[/latex], the mapping for the inverse function is [latex]x-3[/latex].
Inverse function of [latex]f[/latex] = subtract 3.
Notice that the inverse function “undoes” what the original function “does”. The original function “adds 3” to every element in the domain. The inverse function “undoes” “adding 3” by “subtracting 3”. If we apply a function to a domain element [latex]x[/latex], then apply the inverse function to the result, we end up back at [latex]x[/latex].
Try It 4
If [latex]f[/latex] is a function that says. “multiply any real number by 4″,
- create a mapping that using at least four numbers and a variable that describes the function [latex]f[/latex].
- create a mapping that using at least four numbers and a variable that describes the inverse function of [latex]f[/latex].
- describe the inverse function of [latex]f[/latex] in words.
Function Notation
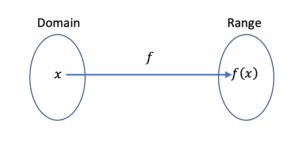
Function notation describes how the elements in the range are obtained from the elements in the domain. Function notation is used because it allows us to immediately recognize the domain variable. The function is given a name that is usually a letter of the alphabet (e.g. f, g, R, C, etc). In parentheses next to the function’s name we write the domain variable. The notation [latex]f(x)[/latex], which is read, “f of x”, means we are going to apply the function named [latex]f[/latex] to the domain variable [latex]x[/latex]. The function [latex]f[/latex] is a rule that tells us how to map the elements in the domain to the elements in the range. It can be written in words, but is usually written in mathematical notation.
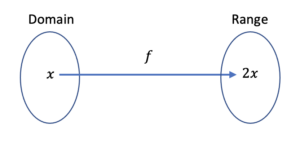
For example, the rule that says, “take any real number and double it” is written in function notation as [latex]f(x)=2x[/latex]. Any element [latex]x[/latex] in the domain is doubled and becomes part of the range.
The notation [latex]f(x)[/latex] specifies that the range element depends on the domain element, [latex]x[/latex]. As [latex]x[/latex] changes value, so does[latex]f(x)[/latex]. Note that the parentheses in function notation do NOT imply multiplication. They simply separate the domain variable from the function name.
Example 3
Write function notation that describes the function:
- Function [latex]f[/latex] when applied to any domain element [latex]x[/latex] adds 4 to the domain element.
- Function [latex]g[/latex] when applied to any domain element [latex]x[/latex] multiplies the domain element by 7.
- Function [latex]C[/latex] when applied to any domain element [latex]t[/latex] squares the domain element.
- Function [latex]H[/latex] when applied to any domain element [latex]z[/latex] multiplies the domain element by -3 and adds 8 to the product.
Solution
- [latex]f(x) = x+4[/latex] The function is named [latex]f[/latex], the variable is [latex]x[/latex] and the rule is “add 4”: [latex]x+4[/latex]
- [latex]g(x) = 7x[/latex] The function is named [latex]g[/latex], the variable is [latex]x[/latex] and the rule is “multiply by 7”: [latex]7x[/latex]
- [latex]C(t) = t^2[/latex] The function is named [latex]C[/latex], the variable is [latex]t[/latex] and the rule is “square”: [latex]t^2[/latex]
- [latex]H(z) = -3z+8[/latex] The function is named [latex]H[/latex], the variable is [latex]z[/latex] and the rule is “multiply by -3 then add 8”: [latex]-3z+8[/latex]
Try It 5
Write function notation that describes the function:
- Function [latex]f[/latex] when applied to any domain element [latex]x[/latex] subtracts 5 from the domain element.
- Function [latex]h[/latex] when applied to any domain element [latex]z[/latex] multiplies the domain element by 3.
- Function [latex]T[/latex] when applied to any domain element [latex]t[/latex] cubes the domain element then add 8.
- Function [latex]G[/latex] when applied to any domain element [latex]x[/latex] adds 7 to the domain element then squares the sum.
Inverse Function Notation
We have already learned that for an inverse function to exist the original function must be one-to-one. This ensures that the inverse is also a function. Rather than having to say, “the inverse function is…”, we use the following notation: The inverse of [latex]f(x)[/latex] is [latex]{f}^{-1}(x)[/latex], which is read, “the inverse of [latex]f(x)[/latex]. This may seem like odd notation as the [latex]-1[/latex] is NOT an exponent. This is because the notation comes from set theory and is a bit of an anomaly. All we need to know right now is that when working with any one-to-one function [latex]f(x),\;{f}^{-1}(x)[/latex] is the inverse of [latex]f(x)[/latex].
Consider the function [latex]f(x)=x+3[/latex]. We already looked at the mapping for this function and its inverse in a previous example:

We write the inverse of [latex]f(x)[/latex] as [latex]{f}^{-1}(x)=x-3[/latex].
Example 4
A one-to-one function [latex]g(x)[/latex] takes whole numbers and squares them.
- Write the function using function notation.
- Create a mapping that shows the function [latex]g[/latex] applied to at least 4 whole numbers and a variable term.
- Create a mapping that shows the inverse of the function [latex]g[/latex] applied to at least 4 whole numbers and a variable term.
- Write the inverse function using function notation.
Solution
- [latex]g(x)=x^2[/latex]
- and 3.

- [latex]{g}^{-1}(x)=\sqrt{x}[/latex]
Try It 6
A one-to-one function [latex]h(x)[/latex] takes integers and divides them by –2.
- Write the function using function notation.
- Create a mapping that shows the function [latex]h[/latex] applied to at least 4 integers and a variable term.
- Create a mapping that shows the inverse of the function [latex]h[/latex] applied to at least 4 integers and a variable term.
- Write the inverse function using function notation.
Try It 7
If a one-to-one function [latex]f(x)[/latex] has a domain of all real numbers and a range of [latex][0, +\infty)[/latex], determine the domain and range of [latex]{f}^{-1}(x)[/latex].
Candela Citations
- Functions. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- All Examples and Try Itd. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. Located at: http://desmos.com. License: CC BY: Attribution


