Learning Objectives
- Evaluate an expression using the order of operations
- Explain the meaning of assigning the independent variable of a function a value
- Solve one-variable linear equations
- Determine function values given a domain value
- Explain the meaning of assigning a function a value
- Determine a domain value given a function value
Before we delve into function values, let’s recall the order of operations to evaluate algebraic expressions.
Order of Operations
When we evaluate algebraic expressions we use the order of operations.
Order of operations
When evaluating algebraic expressions perform the operations in the following order:
1. Grouping Symbols: parentheses ( ), brackets [ ], braces { }, etc.
- Simplify all expressions inside parentheses or other grouping symbols, working on the innermost parentheses first.
2. Exponents and Radicals
- Simplify all expressions with exponents or radicals.
3. Multiplication and Division from left to right
- Perform all multiplication and division in order from left to right. These operations have equal priority.
4. Addition and Subtraction from left to right
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
Operations are applied from left to right within terms of the expression. For example, to evaluate
[latex]6 \div 2 \times 4[/latex]
we perform the division before the multiplication:
[latex]\begin{aligned}&6 \div 2 \times 4\\&=3\times 4\\&=12\end{aligned}[/latex]
Multiplication or division are applied before addition or subtraction. For example, to evaluate
[latex]3+4\times5-6[/latex]
we evaluate [latex]4\times5[/latex] before adding and subtracting:
[latex]\begin{aligned}&3+4\times5-6\\&=3+20-6\\&=23-6\\&=17\end{aligned}[/latex]
If there are any exponents or radicals, we evaluate them before performing any multiplication or division, before performing any addition or subtraction. There is a hierarchy to the operations. For example, to evaluate
[latex]3+5\times3^2[/latex]
we evaluate [latex]3^2[/latex] first:
[latex]\begin{aligned}&3+5\times3^2\\&=3+5\times9\\&=3+45\\&=48\end{aligned}[/latex]
Likewise, to evaluate
[latex]\sqrt{2^3-3(2)+3^2+5}[/latex]
we work under the radical first, following the order of operations:
[latex]\begin{aligned}&\sqrt{2^3-3(2)+3^2+5}\\&=\sqrt{8-6+9+5}\\&=\sqrt{16}\\&=4\end{aligned}[/latex]
Notice that we evaluated each term under the radical separately, but at the same time. This is the most efficient method. Recall that a term is a number (or variable), or a product or quotient of numbers (and variables). Terms are separated by addition and subtraction.
Grouping symbols include parentheses, brackets, braces, and absolute values, and the operations inside these should be performed before any other operations. If there are multiple grouping symbols, the expression should be evaluated from the inside out. For example, to evaluate
[latex]5\times[2+(3\times3^2+1)]\div10[/latex]
we complete the operations inside the parentheses first:
[latex]\begin{aligned}&5\times[2+(3\times3^2+1)]\div10\\&=5\times[2+(3\times9+1)]\div10\\&=5\times[2+(27+1)]\div10\\&=5\times[2+(28)]\div10\\&=5\times[30]\div10\\&=150\div10\\&=15\end{aligned}[/latex]
example 1
Evaluate: [latex]5+{2}^{3}+3\left[6 - 3\left(4 - 2\right)\right][/latex].
Solution
Color is used to show exactly what part of the expression is being evaluated at each step.
[latex]\begin{aligned}&5+\color{blue}{{2}^{3}}+3\left[6 - 3\color{green}{\left(4 - 2\right)}\right]\\&=5+\color{blue}{8}+3\left[6 - 3\color{green}{\left(2\right)}\right]\\&=5+8+3\left[6 - \color{green}{3\left(2\right)}\right]\\&=5+8+3\left[6 - \color{green}{6}\right]\\&=5+8+3\color{green}{\left[6 - 6\right]}\\&=5+8+\color{green}{3\left[0\right]}\\&=5+8+\color{green}{0}\\&=13\end{aligned}[/latex]
Example 2
Evaluate: [latex]\dfrac{-3^2+4\cdot (-6)}{(-5)^2-(6-2)} - \left [\dfrac{6-2^2}{-4}\right ]^{2}[/latex]
Solution
With fractions, we must evaluate the numerator and denominator separately before dividing. We also work each fraction and term separately.
[latex]\begin{aligned}&\dfrac{-\color{blue}{3^2}+\color{green}{4\cdot (-6)}}{\color{red}{(-5)^2}-(\color{blue}{6-2})}-\left [\dfrac{6-\color{blue}{2^2}}{-4}\right ]^{2}&&\text{Evaluate the numerators and denominators separately}\\\\&=\dfrac{-\color{blue}{9}+\color{green}{(-24)}}{\color{red}{25}-(\color{blue}{4})}-\left [\dfrac{6-\color{blue}{4}}{-4}\right ]^{2}&&\text{Evaluate the numerators and denominators separately}\\\\&=\dfrac{-33}{21}-\left [\color{blue}{\dfrac{2}{-4}}\right ]^{2}&&\text{Simplify inside the brackets}\\\\&=\dfrac{-11}{7}-\left [\color{blue}{\dfrac{1}{-2}}\right ]^{2}&&\text{Square}\\\\&=\dfrac{-11}{7}-\color{blue}{\dfrac{1}{4}}&&\text{Common denominator is } 28\\\\&=\dfrac{-11}{7}\color{red}{\times\dfrac{4}{4}}-\dfrac{1}{4}\color{red}{\times\dfrac{7}{7}}&&\text{Build equivalent fractions}\\\\&=\dfrac{-44}{28}-\dfrac{7}{28}&&\text{Multiply}\\\\&=\dfrac{-44-7}{28}&&\text{Combine numerators}\\\\&=-\dfrac{51}{28}&&\text{Subtract}\end{aligned}[/latex]
Try It 1
Evaluate:
1. [latex]4-3[6-(7-4)^2][/latex]
2. [latex]\sqrt{13^2-12^2}-(2+3)^2[/latex]
3. [latex]\dfrac{4^2-3(7-5)}{3(6)+2}-\dfrac{10-2(9-6)^2+6(5)}{2^{(5-2)}}[/latex]
We can also evaluate an algebraic expression if we are given the values assigned to each variable.
Example 3
Evaluate [latex]-x^2+\sqrt{x^2+4x+4}[/latex] when [latex]x=3[/latex].
Solution
We replace every [latex]x[/latex] with the value [latex]3[/latex]. Putting the number inside parentheses helps to ensure we follow the order of operations.
[latex]\begin{aligned}&-\color{blue}{x}^2+\sqrt{\color{blue}{x}^2+4\color{blue}{x}+4}\\&=-\color{blue}{(3)}^2+\sqrt{\color{blue}{(3)}^2+4\color{blue}{(3)}+4}&&\text{Replace each }x\text{ with }(3)\\&=-9+\sqrt{9+12+4}\\&=-9+\sqrt{25}\\&=-9+5\\&=-4\end{aligned}[/latex]
Try It 2
Evaluate [latex]\dfrac{x^2-5x-7}{4x^2-6x-8}[/latex] when [latex]x=-2[/latex].
Assigning the Independent Variable a Value
Determining function values
The algebraic form of a function defines the independent and dependent variables of the function. For example, the function [latex]f(x)=2x+1[/latex], designates [latex]x[/latex] as the the independent variable. We know this because [latex]x[/latex] is the variable in parentheses next to the function name, [latex]f[/latex]. The dependent variable is the function value, and is dependent on the value of the independent variable. The values of the independent variable determine the values of the function (the dependent variable) through the rule described in the algebraic form of the function.
For example, the function[latex]f(x)=2x+1[/latex] has a function value of 1 when the independent variable [latex]x[/latex] is 0. To determine this, we substitute [latex]x=0[/latex] in the function:
[latex]f(x)=2x+1\\f(0) = 2(0) + 1 =1[/latex]
The notation [latex]f(0)[/latex] means the function value (or the value of the dependent variable) given the value of the independent variable [latex]x[/latex] is 0. The function value is 1, after the independent variable in the rule is replaced with 0. Therefore, we may write [latex]f(0)=1[/latex]. Similarly, the function value is 11 after the independent variable in the rule is replaced with 5.
[latex] f(x)=2x+1\\f(5) = 2(5) + 1 = 10 + 1 = 11[/latex]
On the coordinate plane, a function is a graph. The graph is composed of those points [latex](x,y)[/latex] where [latex]x[/latex] is the independent variable and [latex]y=f(x)[/latex] is the dependent variable. Therefore, when assigning the independent variable a value (e.g., [latex]x=5[/latex]), it refers to the point on the graph where the [latex]x[/latex]-coordinate is 5. According to the graph in figure 1, we can determine that the [latex]y[/latex]-coordinate is 11 when the [latex]x[/latex]-coordinate is 5 because the point (5, 11) lies on the graph of the function. The point (5, 11) is the point where the vertical line [latex]x=5[/latex] intersects the graph [latex]y=f(x)[/latex].
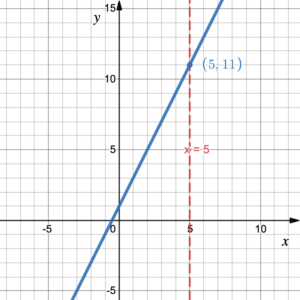
Figure 1.
Example 4
Determine the function values for [latex]g(x)=x^2+3x-2[/latex]:
1. [latex]g(0)[/latex]
2. [latex]g(2)[/latex]
3. [latex]g(–1)[/latex]
Solution
Replace [latex]x[/latex] in the function with each of the values 0, 2, and –1. Inserting the [latex]x[/latex]-values inside parentheses helps keep the order of operations in our minds.
| 1.
[latex]g(x)=x^2+3x-2\\g(0)=(0)^2+3(0)-2=-2[/latex] |
2.
[latex]g(x)=x^2+3x-2\\g(2)=(2)^2+3(2)-2\\g(2)=4+6-2=8[/latex] |
3.
[latex]g(x)=x^2+3x-2\\g(-1)=(-1)^2+3(-1)-2\\g(-1)=1-3-2=-4[/latex] |
Try It 3
Determine the function values for [latex]f(x)=\frac{2x}{x-3}[/latex]:
1. [latex]f(0)[/latex]
2. [latex]f(-2)[/latex]
3. [latex]f(3)[/latex]
Why do you think there is no function value at [latex]x=3[/latex] for the function [latex]f(x)=\frac{2x}{x-3}[/latex]? If we look at the graph, we may gain a better understanding. Figure 2 shows the graph of the rational function [latex]f(x)=\frac{2x}{x-3}[/latex]. The reason that [latex]f(3)[/latex] is undefined is because there is a vertical asymptote at [latex]x=3[/latex]. A graph can never cross a vertical asymptote, so there is no function value at [latex]x=3[/latex].
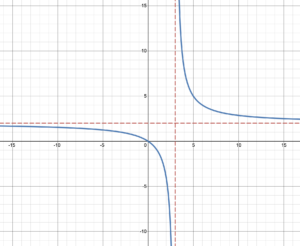
Figure 2. [latex]f(x)=\frac{2x}{x-3}[/latex]
Example 5
Use the graph to determine the function values [latex]f(x)[/latex] at the given [latex]x[/latex]-values.
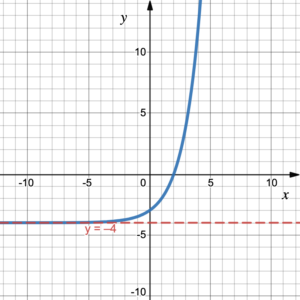
1. [latex]x=0[/latex]
2. [latex]x=1[/latex]
3. [latex]x=-1[/latex]
Solution
1. The line [latex]x=0[/latex] intersects the graph at the point (0, –4) so [latex]f(0) = -4[/latex].
2. The line [latex]x=1[/latex] intersects the graph at the point (1, –2) so [latex]f(1) = -2[/latex].
3. The line [latex]x=-1[/latex] intersects the graph at the point (-1, –4.5) so [latex]f(-1) = -4.5[/latex].
Try It 4
Use the graph to determine the function values [latex]g(x)[/latex] at the given [latex]x[/latex]-values.
1. [latex]x=1[/latex]
2. [latex]x=4[/latex]
3. [latex]x=16[/latex]
Assigning the Function a Value
Determining the value of the independent variable
Graphical Interpretation
On the coordinate plane, when a function is assigned a value, it refers to the point on the graph where the [latex]y[/latex]-coordinate of the point is the assigned value. For example, [latex]f(x)=7[/latex], refers to a point on the graph where the [latex]y[/latex]-coordinate is 7. If we have the graph of the function we can find the corresponding [latex]x[/latex]-value of the function by determining the [latex]x[/latex]-coordinate of the point where [latex]y=7[/latex]. The graph in figure 3 shows that the point (3, 7) lies on the graph of the function. Therefore, when [latex]y=7,\; x=3[/latex]. This means that the function value of 7 occurs when the independent variable value is 3. The point (3, 7) is the point where the horizontal line [latex]y=7[/latex] intersects the graph [latex]y=f(x)[/latex].
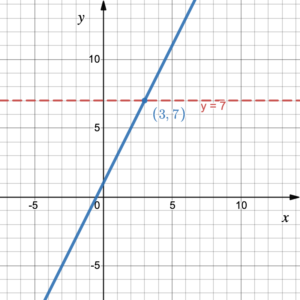
Figure 3. The [latex]x[/latex]-coordinate is 3 when [latex]f(x)=7[/latex]
Example 6
Use the graph of the function [latex]y=f(x)[/latex] to determine the corresponding [latex]x[/latex]-values when:
1. [latex]f(x)=8[/latex]
2. [latex]f(x)=0[/latex]
3. [latex]f(x)=6[/latex]
Solution
1. The point where the horizontal line [latex]y=8[/latex] meets the graph is at the point (–1, 8). Therefore, [latex]x=-1[/latex] when [latex]f(x)=8[/latex].
2. The point where the horizontal line [latex]y=0[/latex] (the [latex]x[/latex]-axis) meets the graph is at the point (3, 0). Therefore, [latex]x=3[/latex] when [latex]f(x)=0[/latex].
3. The point where the horizontal line [latex]y=6[/latex] meets the graph is at the point (0, 6). Therefore, [latex]x=0[/latex] when [latex]f(x)=6[/latex].
Try It 5
Use the graph of the function [latex]y=g(x)[/latex] to determine the corresponding [latex]x[/latex]-values when:
1. [latex]g(x)=4[/latex]
2. [latex]g(x)=0[/latex]
3. [latex]g(x)=-4[/latex]
Algebraic Interpretation
Figure 3 showed the graphical interpretation of solving [latex]f(x)=7[/latex] for [latex]f(x)=2x+1[/latex]. We can also determine the [latex]x[/latex]-value algebraically, by setting [latex]f(x)=7[/latex]:
[latex]\begin{aligned}f(x)&= 2x + 1 \\7&=2x+1\end{aligned}[/latex]
The equation [latex]2x+1=7[/latex] is a linear equation in one variable. In this case the one variable is [latex]x[/latex], and the equation is linear because the highest power on the variable, [latex]x[/latex], is 1 (i.e., [latex]x=x^1[/latex]). Linear equations in one variable can be written in the form [latex]ax+b=c[/latex], where [latex]a, b[/latex], and [latex]c[/latex] are real numbers with [latex]a\ne 0[/latex].
To solve this linear equation (find the value of [latex]x[/latex] that makes the equation true), we must recall the properties of equality:
Properties of Equality
Addition (and Subtraction) Property of Equality
The same term can be added to each side of an equation without changing the solution of the equation:
If [latex]a=b[/latex], then [latex]a+c=b+c[/latex] and [latex]a-c=b-c[/latex].
Multiplication (and Division) Property of Equality
The same non-zero term can be multiplied onto (or divided into) each side of an equation without changing the solution of the equation:
If [latex]a=b[/latex], then [latex]ac=bc[/latex] and [latex]a÷c=b÷c[/latex], [latex]c\ne0[/latex].
Reflection Property
The sides of an equation can be exchanged without changing the solution of the equation:
If [latex]a=b[/latex], then [latex]b=a[/latex].
Consequently, to solve [latex]7=2x+1[/latex], we start by isolating the [latex]x[/latex]-term by subtracting 1 from both sides of the equation:
[latex]\begin{aligned}7&=2x+1\\7\color{blue}{-1}&=2x+1\color{blue}{-1}\\6&=2x\end{aligned}[/latex]
Now we can isolate the variable, [latex]x[/latex], by dividing both sides of the equation by 2:
[latex]\begin{aligned}6&=2x\\6\color{blue}{÷2}&=2x\color{blue}{÷2}\\3&=x\end{aligned}[/latex]
Therefore, using the reflection property, the solution of the equation [latex]7=2x+1[/latex] is [latex]x=3[/latex].
Notice that this is exactly the same solution that we found graphically in figure 3.
This equation solving process to determine the value of an independent variable given a function value will be discussed throughout this entire course.
The goal of solving any equation is to isolate the variable so that the variable (e.g., [latex]x[/latex]) is on one side and a number is on the other side of the equation (e.g., [latex]x=3[/latex]). A general strategy for solving a linear equation is to first simplify the equation by combining like terms on each side of the equation, then use the addition property of equality to get all the variable terms on one side of the equation and all the constant terms (numbers) on the other side of the equation. Finally, after simplifying by combining like terms if necessary, use the multiplication property of equality to isolate the variable.
For example, the equation [latex]3x + 5 - 10 = 4x - 7 + 8x[/latex] can be solved by first combining the constant terms 5 and –10 on the left side and the two variable terms [latex]4x[/latex] and [latex]8x[/latex] on the right side of the equation:
[latex]\begin{aligned}3x+5-10&=4x-7+8x\\3x + \color{blue}{(5 - 10)} &= \color{blue}{(4x +8x)} - 7 \\3x - 5 &= 12x - 7\end{aligned}[/latex]
Now we want all the [latex]x[/latex]-terms on one side and the constant terms on the other side of the equation. To get all the [latex]x[/latex]-terms on the left side of the equation, we subtract [latex]12x[/latex] from both sides of the equation. To get all the numbers on the right side of the equation, we add 5 to both sides:
[latex]\begin{equation}\begin{aligned}3x - 5 &= 12x - 7 \\ 3x - 5 \color{blue}{- 12x} &= 12x - 7\color{blue}{- 12x} \\-9x - 5 &= - 7 \\-9x -5 \color{blue}{+ 5} &= -7\color{blue}{+ 5}\\-9x &= -2\end{aligned}\end{equation}[/latex]
Finally, we can isolate the variable [latex]x[/latex]. Since it is multiplied by [latex]-9[/latex], we divide both sides of the equation by [latex]-9[/latex]:
[latex]\begin{aligned}-9x &= -2\\-9x\color{blue}{\div -9}&=-2\color{blue}{\div -9}\\x&=\dfrac{-2}{-9}\\x&=\dfrac{2}{9}\end{aligned}[/latex].
Therefore, the solution of the equation [latex]3x + 5 - 10 = 4x - 7 + 8x[/latex] is [latex]x=\dfrac{2}{9}[/latex].
Example 7
Solve the equation [latex]13x - 4 = -7x + 6[/latex]
[latex]\begin{aligned}13x - 4 &= -7x + 6 \\13x +7x -4 &= -7x + 7x + 6 \\20x - 4 &= 6 \\20x -4 + 4 &= 6 + 4 \\20x &= 10 \\ \dfrac{20x}{20} &= \dfrac{10}{20} \\ x &= \dfrac{1}{2}\end{aligned}[/latex]
Example 8
Solve the equation [latex]5(2x - 6) + 5x = -2(4x + 1)[/latex]
[latex]\begin{aligned}5(2x - 6) + 5x &= -2(4x + 1) \\ 5 \cdot 2x - 5 \cdot6 + 5x &= (-2) \cdot 4x + (-2) \cdot 1 \\10x - 30 +5x &= -8x - 2 \\15x - 30 &= -8x - 2 \\15x + 8x - 30 &= -8x + 8x - 2 \\ 23x - 30 &= -2 \\23x - 30 + 30 &= -2 + 30 \\23x &= 28 \\ \dfrac{23x}{23} &= \dfrac{28}{23} \\x &= \dfrac{28}{23}\end{aligned}[/latex]
Try It 6
Solve the linear equation [latex]3x-7=-2(x-1)+1[/latex].
Example 9
For [latex]T(x)=-2x+7[/latex], determine the corresponding [latex]x[/latex]-values when:
1. [latex]T(x)=1[/latex]
2. [latex]T(x)=-1[/latex]
3. [latex]T(x)=9[/latex]
Solution
Set [latex]T(x)[/latex] equal to the given values and solve the resulting equation for [latex]x[/latex].
| 1.
[latex]T(x)=-2x+7\\1=-2x+7\\-6=-2x\\3=x[/latex] |
2.
[latex]T(x)=-2x+7\\-1=-2x+7\\-8=-2x\\4=x[/latex] |
3.
[latex]T(x)=-2x+7\\9=-2x+7\\2=-2x\\-1=x[/latex] |
Try It 7
For [latex]T(x)=3x-2[/latex], determine the corresponding [latex]x[/latex]-values when:
1. [latex]T(x)=7[/latex]
2. [latex]T(x)=0[/latex]
3. [latex]T(x)=-11[/latex]
