2.1.2: Parallel and Perpendicular Lines

Learning Objectives

  • Determine the slope between two points on a line
  • Determine if two lines are parallel
  • Determine if two lines are perpendicular

Parallel and Perpendicular Lines

Two lines are said to be parallel if their slopes are the same. This means that the lines are going in exactly the same direction. Two lines are said to be perpendicular if they cross at right angles. Perpendicular lines have slopes that multiply to –1. This means that the slopes are the negative reciprocals of each other.

Graph of parallel lines

Figure 1. Parallel Lines
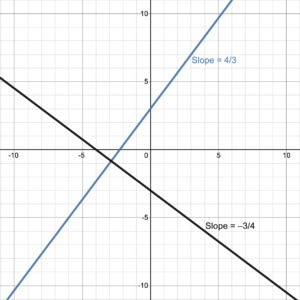
Graph of perpendicular lines

Figure 2. Perpendicular Lines

 

parallel and perpendicular lines

Two lines are parallel if they have the same slope:  [latex]m_1=m_2[/latex]

Two lines are perpendicular if the product of their slopes = –1:  [latex]m_1 \cdot m_2 = -1[/latex]    i.e.  [latex]m_1=\large -\frac{1}{m_2}[/latex] and [latex]m_2=\large -\frac{1}{m_1}[/latex]

Example 1

Determine if the lines are parallel, perpendicular or neither.

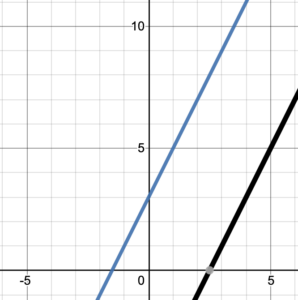
Graph of two lines

Solution

The lines look parallel but let’s find the slopes to be sure.

Blue line passes through (–1, 1) and (0, 3) so has a rise of 2 and a run of 1. Therefore, the slope of the blue line is [latex]m=\frac{\text{rise}}{\text{run}}=2[/latex].

Black line passes through (3, 1) and (5, 5) so has a rise of 4 and a run of 2. Therefore, the slope of the black line is [latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{2}=2[/latex].

Since the slopes are identical, the lines are parallel.

Try It 1

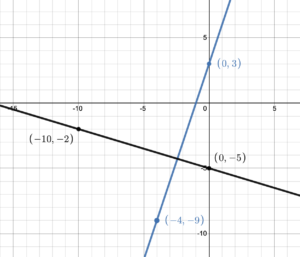
Determine if the lines are parallel, perpendicular or neither.

Graph of 2 lines

Examples 2

Determine if the line that passes through the two points is parallel, perpendicular, or neither to a line with slope –4.

1. (2, 3) and (4, –5)

2. (0, 0) and (1, 4)

3. (–2, 4) and (2, 3)

4. (3, –2) and (7, –1)

Solution

We need to find the slope between the pair of points. If the slope = –4, the line is parallel. If the slope = [latex]\frac{1}{4}[/latex], the line is perpendicular. Otherwise, the line is neither parallel nor perpendicular to a line with slope –4.

1. Rise from 3 to –5 = –8. Run from 2 to 4 = 2.  [latex]m=\frac{\text{rise}}{\text{run}}=\frac{-8}{2}=-4[/latex]. The line is parallel since it has the same slope of –4.

2. Rise from 0 to 4 = 4. Run from 0 to 1 = 1.  [latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{1}=4[/latex]. The line is neither parallel nor perpendicular.

3. Rise from 4 to 3 = –1. Run from –2 to 2 = 4. [latex]m=\frac{\text{rise}}{\text{run}}=\frac{-1}{4}[/latex]. The line is neither parallel nor perpendicular since [latex]\frac{-1}{4} \cdot (-4) = 1 \ne -1[/latex]

4. Rise from –2 to –1 = 1. Run from 3 to 7 = 4.  [latex]m=\frac{\text{rise}}{\text{run}}=\frac{1}{4}[/latex]. The line is perpendicular since [latex]\frac{1}{4} \cdot (-4) = -1[/latex]

Try It 2

Determine if the line that passes through the two points is parallel, perpendicular, or neither to a line with slope [latex]\frac{2}{3}[/latex].

1. (1, 3) and (4, 5)

2. (0, 0) and (–3, –2)

3. (–2, 7) and (0, 4)

4. (3, –5) and (5, –2)