Learning Outcomes
- Explain the meaning of a solution or solutions of a system of linear equations
- Explain the three types of systems of linear equations
- Solve a system of linear equations by graphing
Systems of Equations
A system of linear equations consists of two or more linear equations in two or more variables such that all equations in the system are considered simultaneously. To find the single, unique solution of a system of linear equations, we must find a numerical value for each variable in the system that satisfies all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a single, unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a single, unique solution.
In this section, we will look at systems of linear equations in two variables, which consist of two equations that each contain the same two variables. For example, consider this system of linear equations in two variables:
The solution of a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution of the system of linear equations. We can verify the solution by substituting the value of each variable into each equation to see if the ordered pair satisfies both equations:
This system consists of two linear equations, so graphically, we are considering two lines. Each point on the first line is a solution of the first equation. Each point on the second line is a solution of the second equation. Only a point on both lines will satisfy both equations. For the system we just looked at, the two lines cross at the solution (4, 7), as shown in figure 1.
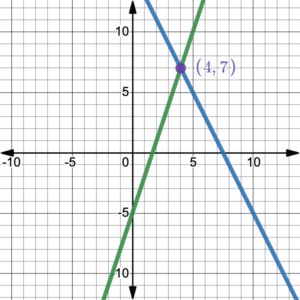
Figure 1. The intersection point of the two lines is the solution of the system.
How To determine whether an ordered pair is a solution of a system
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in each equation; if so, the ordered pair is a solution.
Example 1
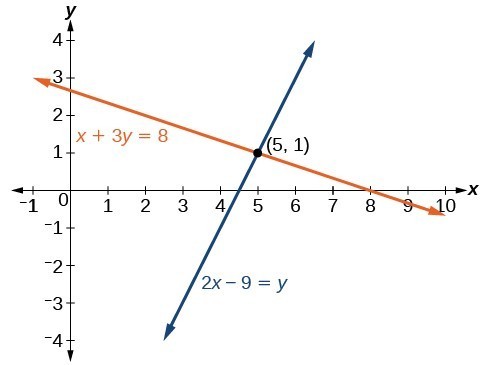
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution of the system of equations:
Solution
Substitute the ordered pair [latex]\left(5,1\right)[/latex] into each equation:
[latex]\begin{array}{ll}\left(5\right)+3\left(1\right)=8\hfill & \hfill \\ \text{ }8=8\hfill & \text{True}\hfill \\2\left(5\right)-9=\left(1\right)\hfill & \hfill \\ \text{ }\text{1=1}\hfill & \text{True}\hfill \end{array}[/latex]
The ordered pair [latex]\left(5,1\right)[/latex] satisfies both equations, so it is the solution of the system.
We can see the solution clearly by plotting the graph of each equation. Since the solution is an ordered pair that satisfies both equations, it is a point on both of the lines and thus the point of intersection of the two lines.
The following video shows another example of how to verify whether an ordered pair is a solution of a system of equations.
Try It 1
Determine whether the ordered pair [latex]\left(–2,4\right)[/latex] is a solution of the system of equations:
[latex]\begin{aligned}-x+2&=y\\2x+y&=8\end{aligned}[/latex]
Classifying a System of Linear Equations in 2 Variables
In addition to considering the number of equations and variables, we can categorize a system of linear equations by the number of solutions it has. A system of equations is said to be consistent if it has at least one solution.
A consistent system is considered to be independent if it has a single solution, like the example we just explored. Graphically, this means that the two lines that make up the system have different slopes and intersect at exactly one point in the plane (e.g., figure 1).
A consistent system is considered to be dependent if the two lines that make up the system have the same slope and the same [latex]y[/latex]-intercept. In other words, the lines coincide, so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions of the system that all lie on the same line.
A system of linear equations is said to be inconsistent if it has no solution. This is where the graph of the system consists of two parallel lines. The lines have the same slope and different [latex]y[/latex]–intercepts. There are no points common to both lines; hence, there is no solution to the system.
Linear Systems of equations
There are three types of systems of linear equations in two variables and three types of solutions.
- A consistent, independent system has exactly one solution. Graphically, the point where the two lines intersect is the only solution.
- A consistent, dependent system has infinitely many solutions. Graphically, the lines coincide. Since they are the same line, every coordinate pair on the line is a solution of the system.
- An inconsistent system has no solution. Graphically, the two lines are parallel and never intersect.
Graphical representations of each type of system:
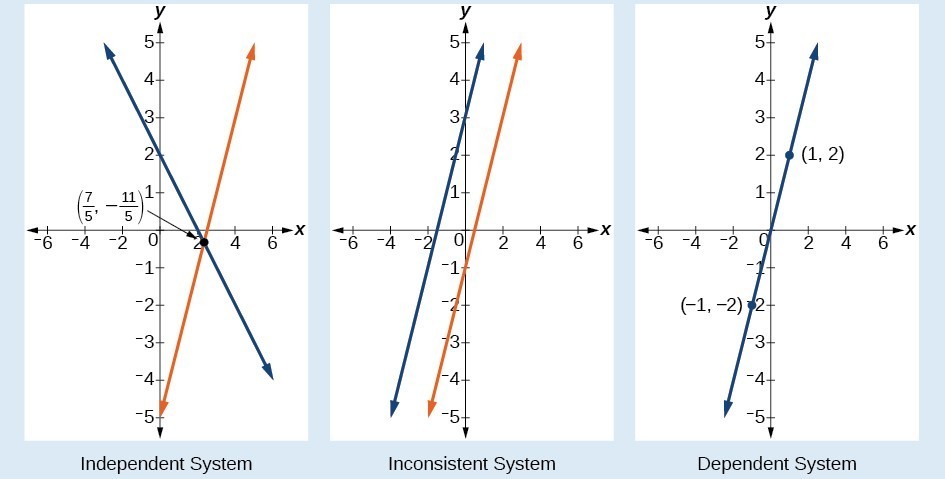
The independent and dependent systems are also consistent because they both have at least one solution.
The following video shows examples of how to identify whether a graphed system has a solution and identify what type of solution is represented.
Example 2
Classify the system of equations shown on the graph:

Solution
The lines are parallel and never cross, therefore there is no solution.
The system is inconsistent.
Try It 2
Classify the system of equations shown on the graph:

Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
Example 3
Solve the following system of equations by graphing. Identify the type of system.
[latex]\begin{array}{c}2x+y=-8\\ x-y=-1\end{array}[/latex]
Solution
To graph the equations, we can either plot points or convert the equation to slope intercept form, [latex]y=mx+b[/latex], and use the slope and [latex]y[/latex]-intercept.
Solve the first equation for [latex]y[/latex]:
[latex]\begin{array}{c}2x+y=-8\\ y=-2x - 8\end{array}[/latex]
So [latex]m=-2[/latex] and the [latex]y[/latex]-intercept is (0, –8).
Solve the second equation for [latex]y[/latex]:
[latex]\begin{array}{c}x-y=-1\\ y=x+1\end{array}[/latex]
So [latex]m=1[/latex] and the [latex]y[/latex]-intercept is (0, 1).
Graph both equations on the same set of axes as seen below.
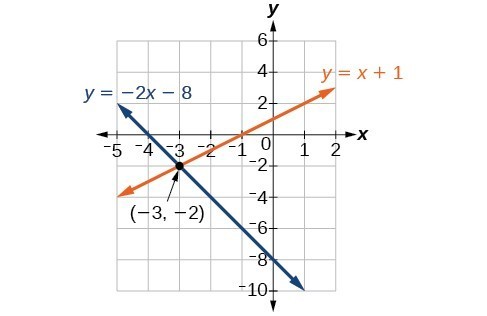
Clearly, the lines intersect at a single point,so the system is independent.
The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex]. We can check to make sure that this is the solution of the system by substituting the ordered pair into each equation:
[latex]\begin{array}{ll}2\left(-3\right)+\left(-2\right)=-8\hfill & \hfill \\ \text{ }-8=-8\hfill & \text{True}\hfill \\ \text{ }\left(-3\right)-\left(-2\right)=-1\hfill & \hfill \\ \text{ }-1=-1\hfill & \text{True}\hfill \end{array}[/latex]
The solution of the system is the ordered pair [latex]\left(-3,-2\right)[/latex].
Try It 3
Solve the system of equations by graphing. Identify the type of system.
[latex]\begin{array}{c}2x+y=6\\ -2x-y=1\end{array}[/latex]
Graphing can be used if the system is inconsistent or dependent. In both cases, we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.
The next video shows how to solve a system of equations by first graphing the lines and then identifying the solution the system has.
Determining the solution of a system of equations graphically does have its drawbacks. Apart from the time it takes to draw the graph, we could end up with a solution whose coordinates are fractions that we cannot read from the graph. Or the lines could look parallel but actually not be parallel.
Example 4
Solve the system of equations by graphing. Identify the type of system.
[latex]\begin{array}{c}2x+3y=6\\ 2x-y=1\end{array}[/latex]
Solution
Using points:
(0, 2) and (3, 0) lie on the line [latex]2x+3y=6[/latex]
(0, –1) and [latex]\left (\frac{1}{2}, 0\right )[/latex] lie on the line [latex]2x-y=1[/latex]
Graph the lines:
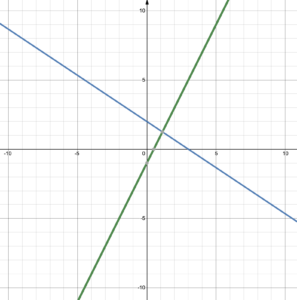
The two lines cross at a single point so there is one solution. This means that the system of equations is consistent and independent.
However, it is impossible to determine the exact solution from the graph as the coordinates are fractional.
This is why algebraic methods are needed to solve systems of equations.
Candela Citations
- Determine if an Ordered Pair is a Solution to a System of Linear Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/2IxgKgjX00k. License: CC BY: Attribution
- Determine the Number of Solutions to a System of Linear Equations From a Graph. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/ZolxtOjcEQY. License: CC BY: Attribution
- Try It: hjm866; hjm482; hjm237. Figure 1. Example of classification. Example with fractional solution.. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Ex 2: Solve a System of Equations by Graphing. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/Lv832rXAQ5k. License: CC BY: Attribution
- Revised and adapted: Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution

