Learning Outcomes
- Solve a system of linear equations using the elimination method
- Write the general solution of a dependent system as an ordered pair in terms of one variable
A third method of solving systems of linear equations is the elimination method. The idea behind this method is to add the two equations in the system together while eliminating one of the variables. The result will be a new linear equation in one variable that we can solve. We get this new equation by adding equations where the same term in each equation has opposite coefficients, so that when they are added the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated through addition.
Example 1
Solve the given system of equations by elimination.
[latex]\begin{equation}\begin{aligned}x+2y&=-1 \\ -x+y&=3 \end{aligned}\end{equation}[/latex]
Solution
Both equations have the [latex]x[/latex] and [latex]y[/latex] terms on the same side of the equations. Notice that the coefficient of [latex]x[/latex] in the second equation, [latex]–1[/latex], is the opposite of the coefficient of [latex]x[/latex] in the first equation, [latex]1[/latex]. This means we can immediately add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant.
Now that we have eliminated [latex]x[/latex], we can solve the resulting equation for [latex]y[/latex]:
[latex]\begin{array}{l}3y=2\hfill \\ \text{ }y=\dfrac{2}{3}\hfill \end{array}[/latex]
Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex]:
[latex]\begin{array}{l}\text{ }-x+y=3\hfill \\ \text{ }-x+\dfrac{2}{3}=3\hfill \\ \text{ }-x=3-\dfrac{2}{3}\hfill \\ \text{ }-x=\dfrac{7}{3}\hfill \\ \text{ }\:\:\:\:\:x=-\dfrac{7}{3}\hfill \end{array}[/latex]
The solution to this system is [latex]\left(-\dfrac{7}{3},\dfrac{2}{3}\right)[/latex].
Check the solution in the first equation:
[latex]\begin{array}{llll}\text{ }x+2y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }\left(-\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right)=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{7}{3}+\dfrac{4}{3}=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{3}{3}=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-1=-1\hfill & \text{True}\hfill \end{array}[/latex]
We gain an important perspective on systems of equations by looking at the graphical representation. In the graph below, we can see that the equations intersect at the solution. We do not need to ask whether there may be a second solution, because observing the graph confirms that the system has exactly one solution.

Notice that we used the second equation to determine [latex]x[/latex] after solving for [latex]y[/latex], then we used the first equation to check our answer. We could have used the first equation to determine [latex]x[/latex] after solving for [latex]y[/latex], then we would have used the second equation to check our answer. We use both equations as we know that the solution will work in the equation we use to determine the second variable, so we use the other one to check that the solution works in both equations.
The following video shows an example of how to use the method of elimination to solve a system of linear equations.
Try It 1
Solve the given system of equations by elimination.
[latex]\begin{equation}\begin{aligned}3x+2y&=6 \\ 3x-2y&=6 \end{aligned}\end{equation}[/latex]
Sometimes we have to do a couple of steps of algebra before we can eliminate a variable from a system and solve it. In the next example, we will see a technique where we multiply one of the equations in the system by a number that will allow us to eliminate one of the variables.
Example 2
Solve the given system of equations by the elimination method.
[latex]\begin{aligned}3x+5y&=-11\hfill \\ x - 2y&=11\hfill \end{aligned}[/latex]
Solution
Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the [latex]x[/latex]-terms will add to zero.
Now, add the equations:
[latex]\begin{array}\ \hfill 3x+5y=−11 \\ \hfill −3x+6y=−33 \\ \text{_____________} \\ \hfill 11y=−44 \\ \hfill y=−4 \end{array}[/latex]
For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex]:
[latex]\begin{array}{c}3x+5y=-11\\ 3x+5\left(-4\right)=-11\\ 3x - 20=-11\\ 3x=9\\ x=3\end{array}[/latex]
Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation.
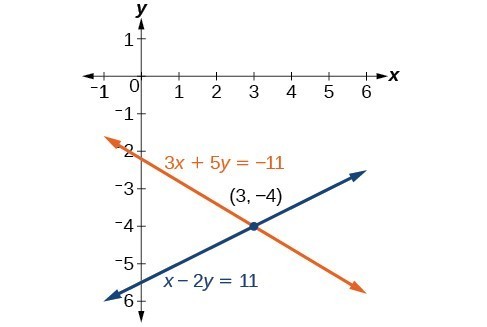
Next is another video example of using the elimination method to solve a system of linear equations.
Try It 2
Solve the given system of equations by the elimination method.
[latex]\begin{aligned}3x+4y&=16\hfill \\ x - 2y&=2\hfill \end{aligned}[/latex]
In the next example, we will see that sometimes both equations need to be multiplied by different numbers in order for one variable to be eliminated.
Example 3
Solve the given system of equations in two variables by elimination.
Solution
If we decide to eliminate [latex]x[/latex], we should notice that one equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. We need to make the coefficients opposites of one another by finding a number that 2 and 5 both divide into. The least common multiple of 2 and 5 is 10, so we will multiply both equations by a constant that will result in the coefficients of [latex]x[/latex] being 10 and –10. We can achieve opposite coefficients of [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex]:
\begin{array}{rl}
\textcolor{blue}{-5}(2x + 3y) &= \textcolor{blue}{-5} \cdot (-16) \\
-10x – 15y &= 80 \\
\\
\textcolor{green}{2}(5x – 10y) &= \textcolor{green}{2} \cdot 30 \\
10x – 20y &= 60
\end{array}
\]
Then, we add the two equations together to eliminate [latex]x[/latex]:
[latex]\begin{array}\ −10x−15y=80 \\ \:\:\,10x−20y=60 \\ \text{______________} \\ \text{ }\:\:\:\:\:\:\:\:\:\:−35y=140 \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:y=−4 \end{array}[/latex]
Substitute [latex]y=-4[/latex] into one of the original equations:
Equation 1:
[latex]\begin{array}{c}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{array}[/latex]
The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the second original equation:
Equation 2:
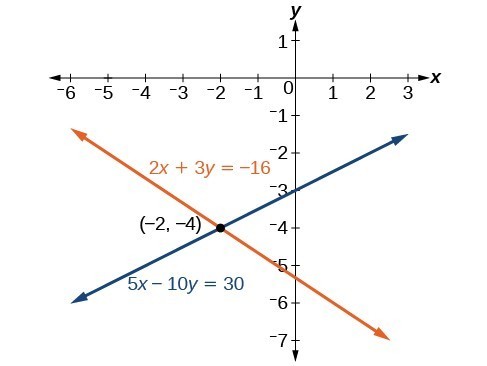
Notice that we checked our solution in the original equations, not the modified equations. This is to guarantee that we did not make an arithmetical mistake when we multiplied the original equations by a constant.
Here is a summary of the general steps for using the elimination method to solve a system of equations.
solve a system of linear equations using the elimination method
- Write both equations with [latex]x[/latex]– and [latex]y[/latex]-terms on the left side of the equals sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. Use multiplication as necessary so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation.
- Add the equations.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the other variable.
- Check the solution by substituting the values into the other original equation.
Try It 3
Solve the given system of equations by the elimination method.
[latex]\begin{aligned}5x+-2y&=20\hfill \\ 3x + 5y&=-19\hfill \end{aligned}[/latex]
In the next example, we will show how to solve a system with fractions. The easiest way to solve this system is to clear the fractions first by multiplying the equation by the least common denominator.
Example 4
Solve the given system of equations in two variables by elimination.
[latex]\begin{array}{l}\dfrac{x}{3}+\dfrac{y}{6}=3\hfill \\ \dfrac{x}{2}-\dfrac{y}{4}=\text{ }1\hfill \end{array}[/latex]
Solution
First clear each equation of fractions by multiplying both sides of the equation by the least common denominator:
\[
\begin{array}{rl}
\textcolor{blue}{6} \left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= \textcolor{blue}{6} \cdot 3 \\
2x + y &= 18 \\
\\
\textcolor{blue}{4} \left(\dfrac{x}{2}-\dfrac{y}{4}\right) &= \textcolor{blue}{4} \cdot 1 \\
2x – y &= 4
\end{array}
\]
Now multiply the second equation by [latex]-1[/latex] so that we can eliminate the [latex]x[/latex]-term:
\[
\begin{array}{rl}
\textcolor{blue}{-1} (2x – y) &= \textcolor{blue}{-1} \cdot 4 \\
-2x + y &= -4
\end{array}
\]
Add the two equations to eliminate the [latex]x[/latex]-terms and solve the resulting equation:
[latex]\begin{array}\ \hfill 2x+y=18 \\ \hfill−2x+y=−4 \\ \text{_____________} \\ \hfill 2y=14 \\ \hfill y=7 \end{array}[/latex]
Substitute [latex]y=7[/latex] into the first equation, and solve for [latex]x[/latex]:
[latex]\begin{array}{l}2x+\left(7\right)=18\hfill \\ \text{ }2x=11\hfill \\ \text{ }x=\dfrac{11}{2}\hfill \end{array}[/latex]
The solution is [latex]\left(\dfrac{11}{2},7\right)[/latex]. Check it in the other equation.
[latex]\begin{array}{c}2x-y=4\\ 2(\dfrac{11}{2})-7=4\\ 11-7=4 \\ 4=4\end{array}[/latex]
The following video shows another example of using the elimination method to solve a system; this one has coefficients that are fractions.
Try It 4
Solve the given system of equations by the elimination method.
[latex]\begin{aligned}x+\frac{1}{5}y&=4\hfill \\ \frac{1}{2}x + y&=11\hfill \end{aligned}[/latex]
The elimination method can also identify dependent systems and inconsistent systems. If after adding to eliminate one of the terms, the resulting equation is an identity such as 0=0, the system is dependent, and if the resulting equation is a contradiction such as 5 = 8, the system is inconsistent.
EXAMPLE 5
Find a solution to the system of equations using the elimination method.
.
[latex]\begin{array}{c}x+3y=2\\ 3x+9y=6\end{array}[/latex]
Solution
With the elimination method, we want to eliminate one of the variables by adding the equations.
Let’s focus on eliminating [latex]x[/latex]. If we multiply both sides of the first equation by [latex]-3[/latex], then we will be able to eliminate the [latex]x[/latex] -variable by addition:
[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \left(-3\right)\left(x+3y\right)=\left(-3\right)\left(2\right)\hfill \\ \text{ }-3x - 9y=-6\hfill \end{array}[/latex]
Now add the equations:
[latex]\begin{array} \hfill−3x−9y=−6 \\ \hfill3x+9y=6 \\ \hfill \text{_____________} \\ \hfill 0=0 \end{array}[/latex]
We end up with an identity which means that there will be an infinite number of solutions that satisfy both equations.
Answer
There are an infinite number of solution that lie on the line [latex]x+3y=2[/latex].
Note: If we rewrite both equations in slope-intercept form, we end up with the same equation.
[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \text{ }3y=-x+2\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \\ 3x+9y=6\hfill \\ \text{ }9y=-3x+6\hfill \\ \text{ }y=-\dfrac{3}{9}x+\dfrac{6}{9}\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \end{array}[/latex]
The graph shows that both lines are the same.
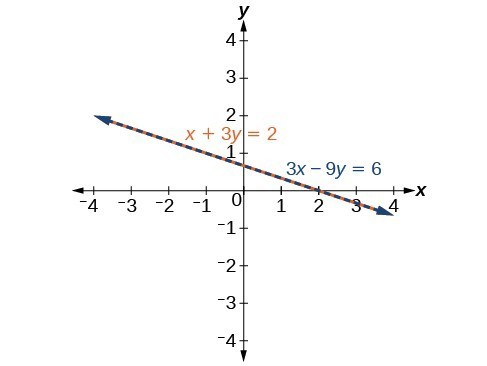
Notice that when we have a dependent system we write the set of all solutions as an ordered pair in term of one variable. In the example, we wrote [latex]y[/latex] in terms of [latex]x[/latex] and wrote the solution as [latex]\left(x, -\dfrac{1}{3}x+\dfrac{2}{3}\right)[/latex]. We could also have written the solution in terms of [latex]y[/latex]: [latex]\left (-3y+2, y\right )[/latex].
The following video shows another example of solving a system that is dependent using elimination.
The last video example presents a system that is inconsistent; it has no solutions, which means the lines the equations represent are parallel to each other, and the system is inconsistent.
Try It 5
Solve the system of equations using the elimination method.
[latex]\begin{aligned}\frac{5}{2}x-y&=4\\-\frac{5}{4}x+\frac{1}{2}y&=5\end{aligned}[/latex]
Try It 6
Solve the system of equations using the elimination method.
[latex]\begin{aligned}\frac{2}{3}x-\frac{1}{4}y&=-1\\-6x+\frac{9}{4}y&=9\end{aligned}[/latex]
Candela Citations
- Adapted and revised. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Try It hjm487; hjm827; hjm507; hjm036; hjm553; hjm239. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Ex 1: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/M4IEmwcqR3c. License: CC BY: Attribution
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/_liDhKops2w. License: CC BY: Attribution
- Ex: Solve a System of Equations Using Eliminations (Fractions). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/s3S64b1DrtQ. License: CC BY: Attribution
- Ex: System of Equations Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/NRxh9Q16Ulk. License: CC BY: Attribution
- Ex: System of Equations Using Elimination (No Solution). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/z5_ACYtzW98. License: CC BY: Attribution
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
