Learning Outcomes
- Use back substitution to find a solution to a system of linear equations in three variables
- Solve a system of linear equations in three variables
We know how to solve a system of two linear equations in two variables. So our goal in solving a system of three linear equations in three variable is to simplify it to a system of two linear equations in two variables. In order to to this we need to eliminate a variable by working with two pairs of equations to eliminate the same variable in each pair. By doing this we will end up with two new equations in two variables that we already know how to solve. Solving this new system will result in determining the values of two of the variables. We can then find the remaining variable by substitution.
SOLVING a linear system of three equations
- Pick any pair of equations and eliminate one variable using the elimination (addition) method.
- Pick another pair of equations and eliminate the same variable using the elimination (addition) method.
- Solve the resulting system of the two new equations.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Solving a system with three variables is very similar to solving one with two variables. It is important to keep track of our work as the addition of one more equation creates more steps in the solution process.
We’ll take the steps slowly in the following few examples. First, we’ll look just at the last step in the process: back-substitution. Then, we’ll look at an example that requires the elimination (addition) method to reach the first solution. We have also included some video examples that illustrate some of the different kinds of situations we may encounter when solving three-by-three systems.
In the example that follows, we will solve the system by using back-substitution.
Example 1
Solve the system of linear equations.
[latex]\left\lbrace\begin{array}{rrrrrrr}x&-&\dfrac{1}{3}y&+&\dfrac{1}{2}z&=&1\\&{}&y&-&\dfrac{1}{2}z&=&4\\&{}&{}&{}&{}z&=&-1\end{array}\right.[/latex]
Solution
The third equation states that [latex]z = −1[/latex], so we substitute this into the second equation to obtain a value for [latex]y[/latex].
[latex]\begin{aligned}y-\dfrac{1}{2}z&=4\\y-\dfrac{1}{2}(-1)&=4\\y+\dfrac{1}{2}&=4\\y&=4-\dfrac{1}{2}\\y&=\dfrac{8}{2}-\dfrac{1}{2}\\y&=\dfrac{7}{2}\end{aligned}[/latex]
Now we have two of our values, and we can substitute them both into the first equation to solve for [latex]x[/latex].
[latex]\begin{aligned}x-\dfrac{1}{3}y+\dfrac{1}{2}z&=1\\x-\dfrac{1}{3}\left(\dfrac{7}{2}\right)+\dfrac{1}{2}\left(-1\right)&=1\\x-\dfrac{7}{6}-\dfrac{1}{2}&=1\\x-\dfrac{7}{6}-\dfrac{3}{6}&=1\\x-\dfrac{10}{6}&=1\\x&=1+\dfrac{10}{6}\\x&=\dfrac{6}{6}+\dfrac{10}{6}\\x&=\dfrac{16}{6}\\x&=\dfrac{8}{3}\end{aligned}[/latex]
Now we have our ordered triple; remember to place each variable value in order.
[latex](x,y,z)=\left(\dfrac{8}{3},\dfrac{7}{2},-1\right)[/latex]
Analysis of the Solution:
Each of the lines in the system above represents a plane. If you imagine three stiff sheets of paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.
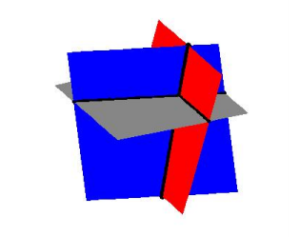
Three planes intersecting.
The following video shows another example of using back-substitution to solve a linear system in three variables.
Try It 1
Solve the system of linear equations.
[latex]\left\lbrace\begin{array}{rrrrrrr}2x&+&3y&-&z&=&-1\\&&2y&+&3z&=&-3\\&&&&z&=&1\end{array}\right.[/latex]
In the next example we’ll need to use the elimination method to find our first solution.
Example 2
Find a solution to the following system:
Solution
We labeled the equations this time to be able to keep track of things a little more easily.
Looking at the equations we see that equations (2) and (3) have only two variables. So we will solve this system by adding them together to eliminate [latex]y[/latex] and solve for [latex]z[/latex]:
Now we can substitute in 6 for [latex]z[/latex] in equation (2):
[latex]\begin{aligned}-2y+(6)&=6\\-2y&=6-6\\-2y&=0\\y&=0\end{aligned}[/latex]
NOTE: Be careful here not to get confused with a solution of [latex]y = 0[/latex] and an inconsistent solution. It is ok for variables to equal [latex]0[/latex].
Now we can substitute [latex]z = 6[/latex] and [latex]y = 0[/latex] into equation (1) and solve for [latex]x[/latex]:
[latex]\begin{aligned}x-y+z&=5\\x-0+6&=5\\x+6&=5\\x&=5-6\\x&=-1\end{aligned}[/latex]
Answer
[latex](x,y,z)=(-1,0,6)[/latex]
Watch the following videos for more examples of the algebra that may be encountered when solving systems with three variables.
Solving three-by-three systems involves both creativity and careful, well-organized work. It may take some practice before it begins to feel natural.
Example 3
Solve the system of linear equations:
[latex]\left\lbrace\begin{array}{rrrrrrr}x&-& 2y&+&3z&=&9\\ -x&+&3y&-&z&=&-6\\ 2x&-&5y&+&5z&=&17 \end{array}\right.[/latex][latex]\hspace{5mm}\begin{gathered}\text{(1})\\ \text{(2)}\\ \text{(3)}\end{gathered}[/latex]
Solution
There will always be several choices as to where to begin. Look for the variable that can be eliminated most easily from two pairs of equations. Let’s start by eliminating [latex]x[/latex]:
Add equations (1) and (2):
[latex]\begin{array}{rrrrrrr}x &-& 2y&+&3z&=&9\\ -x&+&3y&-&z&=&-6 \\ \hline &&y&+&2z&=&3 \end{array}[/latex][latex]\hspace{5mm}\begin{gathered}\text{(1})\\ \text{(2)}\\ \text{(4)}\end{gathered}[/latex]
The result is a new equation in two variables that we’ve labeled as equation (4).
Now choose another pair of the original equations to eliminate [latex]x[/latex]:
Using equations (1) and (3):
We need to multiply equation (1) by [latex]-2[/latex] and add the result to equation (3).
[latex]\begin{array}{rrrrrrr}−2x&+&4y&−&6z&=&−18 \\ 2x&−&5y&+&5z&=&17 \\ \hline &−&y&−&z&=&−1\end{array}[/latex][latex]\hspace{5mm}\begin{align}&\text{(2) multiplied by }−2\\&\left(3\right)\\&(5)\end{align}[/latex]
The result is equation (5). Equations (4) and (5) now form a system of two linear equations in the two variables y and z:
We can solve for [latex]z[/latex] by adding equations (4) and (5):
[latex]\begin{array}{rrrrr}y&+&2z&=&3 \\ -y&-&z&=&-1 \\ \hline &&z&=&2 \end{array}[/latex][latex]\hspace{5mm}\begin{align}(4)\\(5)\\(6)\end{align}[/latex]
Now we know the value of [latex]x[/latex], we can substitute into either equation (4) or (5) to find [latex]y[/latex].
Back-substitute [latex]z=2[/latex] into equation (4) and solve for [latex]y[/latex]:
[latex]\begin{align}y+2\left(2\right)&=3 \\ y+4&=3 \\ y&=-1 \end{align}[/latex]
Knowing the values of [latex]z[/latex] and [latex]y[/latex] allows us to back-substitute [latex]z=2[/latex] and [latex]y=-1[/latex] into equation (1). This will yield the solution for [latex]x[/latex]:
[latex]\begin{align} x - 2\left(-1\right)+3\left(2\right)&=9\\ x+2+6&=9\\ x&=1\end{align}[/latex]
Answer
The solution is the ordered triple [latex]\left(1,-1,2\right)[/latex].
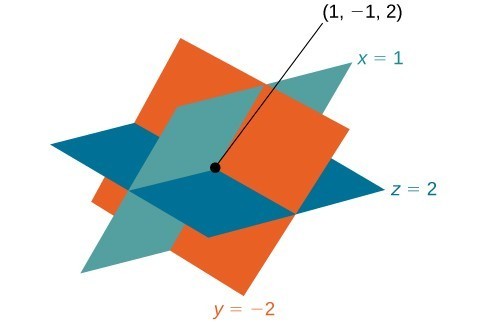
TRY IT 2
In the following video, you will see a visual representation of the three possible outcomes for solutions to a system of equations in three variables. There is also a worked example of solving a system using elimination.
Dependent and Inconsistent Systems
When solving a system of equations algebraically, we know we have a dependent system when we get an equation that is an identity (e.g., 0 = 0). We also know that if we end up with a contradiction, the system is inconsistent, and there is no solution.
Example 4
Solve the following system.
[latex]\left\lbrace\begin{array}{rrrrrrr}x&-&3y&+&z&=&4\\{}&-&y&-&4z&=&7\\{}&&2y&+&8z&=&-12\end{array}\right.[/latex][latex]\hspace{5mm}\begin{gathered}\text{(1})\\ \text{(2)}\\ \text{(3)}\end{gathered}[/latex]
Solution
First notice that equations (2) and (3) have no [latex]x[/latex]-term. So we can solve them to find [latex]y[/latex] and [latex]z[/latex].
To eliminate [latex]y[/latex] using equations (2) and (3), we can multiply equation (2) by 2 and add equations (2) and (3) together:
First, multiply both sides of equation (2) by 2:
[latex]\begin{array}{rrrrr}\color{blue}{2}(-y&-&4z)&=&\color{blue}{2}(7)\\-2y&-&8z\,&=&14\end{array}[/latex]
Next, add equations [latex](2)[/latex] and [latex](3)[/latex] together to eliminate y and solve for [latex]z[/latex].
[latex]\begin{array}{rrrrr}-2y&-&8z&=&14\\2y&+&8z&=&-12\\ \hline 0&+&0&=&2\\&{}&0&=&2\end{array}[/latex]
We have a contradiction so the two planes represented by equations (2) and (3) are parallel.
This means there is no solution to the system of equations.
The next video shows another example of using elimination to solve a system in three variables that ends up being inconsistent and having no solution.
We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. The other possibility is that two of the equations could be the same and intersect the third on a line.
Example 5
Find the solution to the given system of three equations in three variables.
[latex]\left\lbrace\begin{array}{rrrrrrr}2x&+&y&-&3z&=&0& \hfill \left(1\right)\\ 4x&+&2y& - &6z&=&0& \hfill \left(2\right)\\ x&-&y&+&z&=&0& \hfill \left(3\right)\end{array}\right.[/latex]
Solution
First, we decide which variable looks easiest to eliminate: [latex]y[/latex]
We can multiply equation [latex](1)[/latex] by [latex]-2[/latex] and add it to equation [latex](2)[/latex]:
[latex]\begin{array}{rrrrrl} −4x&−&2y&+&6z&=&0 \hfill&(1)\text{ multiplied by }−2 \\ 4x&+&2y&−&6z&=&0\hfill&(2) \end{array}[/latex]
The result we get when adding the two equations is an identity, [latex]0=0[/latex] which tells us that the two planes represented by equations (1) and (2) are coincidental.
We now need to determine if the third plane is a) coincidental with the first two (in which case there are infinite solutions on the plane), or b) parallel to the coincident planes (in which case the system has no solution), or c) intersects with the two coincidental planes in a line (in which case there are infinite solutions on the line).
SInce equations (1) and (2) are equivalent, we can use either one with equation (3) to help make our determination.
Let’s consider equations (1) and (3). If we add (1) and (3) together, the [latex]y[/latex]-terms will cancel each other out:
[latex]\begin{array}{rrrrrrr}2x&+&y&-&3z&=&0& \hfill \left(1\right)\\ x&-&y&+&z&=&0& \hfill \left(3\right)\\ \hline3x&&&-&2z&=&0&\end{array}[/latex]
This is a linear equation in the two variables {latex]x[/latex] and [latex]z[/latex], so the two coincident planes intersect the third plane in a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.
The last video example shows a dependent system that has an infinite number of solutions. It is enough for this course to know why the system is dependent. The video goes on to discuss how to write all variables in term of a parameter. Although that is not covered in this class, we will see it in College Algebra.
It is important to know why a system of linear equations in three variables is dependent. The infinite solutions to such a system do not just float around anywhere in space! Rather they are either all on a line or on a plane.
The infinite solutions will be on a line if two of the three equations are equivalent. Graphically, this means that two of the planes are identical and the third plane crosses them in a line.
The infinite solutions will be on a line if the three planes meet in a single line.
The infinite solutions will be on a plane if all three equations are equivalent. Graphically this means that all three planes coincide and it is this plane that is the solution set.
IMPORTANT NOTE: When we get an identity from manipulating two equations, that does not mean that there are automatically an infinite number of solutions! It simply means that two of the three planes are coincident. We still need to determine whether the third plane is also coincident (resulting in infinite solutions on the three coincident planes), is parallel to the two coincident planes (resulting in no solution), or intersects the two coincident planes in a line (resulting in infinite solutions on the line of intersection).
Try It 3
Solve the system of linear equations:
[latex]\left\lbrace\begin{array}{rrrrrrr}2x&-&3y&+&4z&=&9\\x&+&5y&-&3z&=&12\\-4x&+&6y&-&8z&=&-18\end{array}\right.[/latex]
Try It 4
Solve the system of linear equations:
[latex]\left\lbrace\begin{array}{rrrrrrr}2x&-&3y&+&4z&=&9\\2x&-&3y&+&4z&=&12\\-4x&+&6y&-&8z&=&-5\end{array}\right.[/latex]
