The Composition of a Function and Its Inverse

In the previous section we discovered that a one-to-one function has an inverse function, and that a one-to-one function and its inverse functions are reflections of one another across the line $y=x$. This means that while the green curve in figure 1 is the inverse function of the blue curve, symmetry shows that the blue curve must be the inverse function of the green curve.

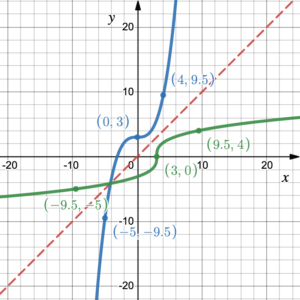
Figure 1. A one-to-one function and its inverse functions are reflections of each other across the line $y=x$

In figure 1, if $y=f(x)$ is the blue curve, $f(0) = 3$ implies that $f^{-1}(3) = 0$. This is confirmed on the green curve $y=f^{-1}(x)$. In other words, if we find the function value at $x=0$ and get 3, then find the inverse function value at $x=3$, $f^{-1}(3)$, we get back to 0. The inverse function undoes the original function and we end up back where we started.

Logically, since $f(x)$ and $f^{-1}(x)$ are inverse functions of each other, $\left (f\circ f^{-1}(x)\right )=f\left (f^{-1}(x)\right )=x$.

Diagrammatically,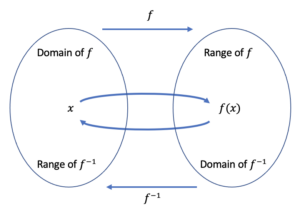 

Given a function $f\left(x\right)$, we can verify whether some other function $g\left(x\right)$ is the inverse of $f\left(x\right)$ by checking whether $g\left(f\left(x\right)\right)=x$ and $f\left(g\left(x\right)\right)=x$ are true.

For example, prove that $y=4x$ and $y=\frac{1}{4}x$ are inverse functions.

$\left({f}^{-1}\circ f\right)\left(x\right)={f}^{-1}\left(4x\right)=\frac{1}{4}\left(4x\right)=x$

and

$\left({f}^{}\circ {f}^{-1}\right)\left(x\right)=f\left(\frac{1}{4}x\right)=4\left(\frac{1}{4}x\right)=x$