3.4.1: The Division of Polynomials

Learning Outcomes

Divide a polynomial by a monomial
Use long division to divide polynomials

Dividing a Polynomial by a Monomial

The distributive property of multiplication over addition also works for division, since division is just multiplication by the reciprocal.

The distributive property

$a(b+c)=ab+ac$

$\dfrac{a+b}{c}=\dfrac{1}{c}(a+b)=\dfrac{a}{c}+\dfrac{b}{c}$

where $a,\;b,$ and $c$ are algebraic terms.

To divide a polynomial by a monomial, we can write the division as a fraction, and then decompose the fraction into the sum of fractions, and then simplify each fraction. For example, to divide the polynomial $3x^3-6x^2+18x-7$ by $2x^2$ :

$\begin{aligned}&\;\;\;\;\,\dfrac{3x^3-6x^2+18x-7}{2x^2} \\ \\&= \dfrac{3x^3}{2x^2}-\dfrac{6x^2}{2x^2}+\dfrac{18x}{2x^2}-\dfrac{7}{2x^2} \\ \\&= \dfrac{3}{2}x-3+\dfrac{9}{x}-\dfrac{7}{2x^2}\end{aligned}$

Example 1

Divide $12x^4-18x^3+36x^2-24x$ by $-6x^2$ .

Solution

Divide each term in the first polynomial by the monomial divisor:

$\begin{aligned}&\;\;\;\;\,\dfrac{12x^4-18x^3+36x^2-24x}{-6x^2}\\ \\&=\dfrac{12x^4}{-6x^2}-\dfrac{18x^3}{-6x^2}+\dfrac{36x^2}{-6x^2}-\dfrac{24x}{-6x^2}\\ \\&=-2x^2+3x-6+\dfrac{4}{x}\end{aligned}$

Try It 1

Divide $60x^5-30x^4+25x^3-35x+10$ by $10x^3$ .

Show Answer

$6x^2-3x+\dfrac{5}{2}-\dfrac{7}{2x^2}+\dfrac{1}{x^3}$

Dividing Polynomials using Long Division

long division revision

When we divide two numbers, we often end up with a remainder. For example, $17\div 3 = 5\;\text{R}(3)$ .

This can also be thought of as:

$\dfrac{17}{3}=5+\dfrac{2}{3}$

Equivalently, multiplying both sides by 3:

$17=3\cdot 5 + 2$

The process used to accomplish division of polynomials is similar to long division of whole numbers, so it is essential that we are confident with long division of whole numbers. If you haven’t performed long division for a while, take a moment to refresh before reading this section.

The Long Division Algorithm for Arithmetic

We begin by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat. For example, let’s divide 178 by 3 using long division.

Long Division. Step 1, 5 times 3 equals 15 and 17 minus 15 equals 2. Step 2: Bring down the 8. Step 3: 9 times 3 equals 27 and 28 minus 27 equals 1. Answer: 59 with a remainder of 1 or 59 and one-third.

Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.

$\begin{aligned}\left(\text{Divisor }\cdot \text{Quotient}\right)\text{ + Remainder}&=\text{Dividend}\\ \left(3\cdot 59\right)+1&= 178\end{aligned}$

We call this the Division Algorithm:

$\dfrac{\text{Dividend}}{\text{Divisor}}=\text{Quotient}+\dfrac{\text{Remainder}}{\text{Divisor}}$

Equivalently:

$\text{Dividend}=\text{Quotient}\cdot\text{Divisor}+\text{Remainder}$

The dividend, divisor, and remainder are whole numbers, and the remainder < divisor.

Example 2

Use long division to divide: $\dfrac{242}{15}$

Solution

$\begin{aligned}16\\15) \overline{242}\\15\;\;\\ \overline{92}\\ 90\\ \overline{2}\end{aligned}$

So, $\dfrac{242}{15}=16 +\dfrac{2}{15}$

Equivalently, $242=15\cdot 16 + 2$

Try It 2

Use long division to divide: $\dfrac{463}{12}$

Show Answer

$\dfrac{463}{12}=38+\dfrac{7}{12}$

The Division Algorithm

The division algorithm for arithmetic can be adapted to polynomials.

division algorithm for polynomials

Let $p(x)$ and $d(x)$ be polynomials where the degree of $p(x)$ ≥ the degree of $d(x)$ , then

$\dfrac{p(x)}{d(x)}=q(x)+\dfrac{r(x)}{d(x)}$

where the degree of $r(x)$ < the degree of $d(x)$ .

Equivalently, multiplying both sides by $d(x)$ :

$p(x)=d(x)q(x) + r(x)$

The division algorithm allows us to divide two polynomials. To set up this division there are two basic rules that must be adhered to:

The polynomials of the divisor and dividend need to be in descending order, which means the terms of a polynomial are written in the order of descending powers of variables.
There should be no gaps in the descending order of powers. Any gaps need to be filled with zeros.

For example, if the dividend is given as $4+5x-3x^3$ , the first step tells us to write the polynomial in descending order:

$-3x^3+5x+4$

Since there is no $x^2$ term in this polynomial (i.e. there is a gap), we must include $0x^2$ as a term to fill the gap:

$-3x^3\color{blue}{+0x^2}+5x+4$

Example 3

Write the polynomial in descending order, filling any gaps with zeros.

1. $7x^3-8+2x^2$

2. $6x-4x^2-3x^3+x^5$

Solution

1. First write $7x^3-8+2x^2$ in descending order: $7x^3+2x^2-8$

Now look for missing terms: there is no $x$ term. Write $0x$ where the $x$ term should be:

$7x^3+2x^2\color{blue}{+0x}-8$

2. First write $6x-4x^2-3x^3+x^5$ in descending order: $x^5-3x^3-4x^2+6x$

Now look for missing terms: there is no $x^4$ term and no constant term. Write $0x^4$ where the $x^4$ term should be, and write 0 for the constant term at the end of the polynomial:

$x^5\color{blue}{+0x^4}-3x^3-4x^2+6x\color{blue}{+0}$

Try It 3

Write the polynomial in descending order, filling any gaps with zeros.

1. $7x^4-8x+2x^2$

2. $-2x-4x^4-3x^3+x^5$

Show Answer

$7x^4\color{blue}{+0x^3}+2x^2-8x\color{blue}{+0}$
$x^5-4x^4-3x^3\color{blue}{+0x^2}-2x\color{blue}{+0}$

The process for dividing polynomials is basically the same as it was for whole numbers.

As an example, let’s divide

x^{2} + x + 1

$x^2+x+1$ by

x - 1

$x-1$ .

We truncate the divisor $x-1$ to $x$ and divide the first term in the dividend by $x$ : $\dfrac{x^2}{x}=x$ . This $\color{blue}{x}$ goes on the quotient line.

Now multiply $\color{blue}{x}$ by the divisor $x-1$ : $\color{blue}{x}\cdot(x-1)=\color{blue}{x^2-x}$ . This goes under the dividend.

Now subtract: $(x^2+x+1)-(\color{blue}{x^2-x})=(x^2-x^2)+(x-(-x))+1=\color{red}{2x+1}$ .

Divide $2x$ by $x$ : $\dfrac{2x}{x}=\color{green}{2}$ . Add this $\color{green}{2}$ onto the quotient line.

Multiply $\color{green}{2}$ by the divisor $x-1$ : $\color{green}{2}(x-1)=\color{green}{2x-2}$ .

FInally, subtract: $\color{red}{(2x+1)}-\color{green}{(2x-2)}=(\color{red}{2x}-\color{green}{2x})+(\color{red}{1}-(\color{green}{-2}))=\color{orange}{3}$ .

We have found that $\dfrac{x^2+x+1}{x-1}=x+2+\dfrac{3}{x-1}$ .

\begin{matrix} x + 2 x - 1) ¯ ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯ x^{2} + x + 1 x^{2} - x ¯ ¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯ 2 x + 1 2 x - 2 - ----- - 3 \end{matrix}

$\begin{aligned}\color{blue}{x}+\color{green}{2}\\x-1 )\overline{x^2+x+1}\\ \color{blue}{x^2-x}\;\;\;\;\;\;\\ \overline{\color{red}{2x+1}}\\\underline{\color{green}{2x-2}}\\ \color{orange}{3}\end{aligned}$

We can identify the dividend, divisor, quotient, and remainder by writing this answer in its equivalent form:

$\begin{array}{lllllll}&x^2+x+1&=&(x-1)&(x+2)&+&3\\&\text{Dividend}&&\text{Divisor}&\text{Quotient}&&\text{Remainder}\end{array}$

Example 4

Divide $2{x}^{3}-3{x}^{2}+4x+5$ by $x+2$ using the long division algorithm.

Solution

Answer

$\dfrac{2{x}^{3}-3{x}^{2}+4x+5}{x+2}=2{x}^{2}-7x+18+\dfrac{-31}{x+2}$

or equivalently,

$2{x}^{3}-3{x}^{2}+4x+5=\left(x+2\right)\left(2{x}^{2}-7x+18\right)+(-31)$

We can identify the dividend, divisor, quotient, and remainder.

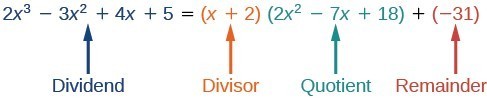
The dividend is 2x cubed minus 3x squared plus 4x plus 5. The divisor is x plus 2. The quotient is 2x squared minus 7x plus 18. The remainder is negative 31.

Notice that the remainder in this example is negative. Even when the remainder is negative, we add it as a negative remainder.

using long division to divide polynomials

Set up the division problem based on the rules of descending powers and no gaps.
Determine the first term of the quotient by dividing the leading term of the dividend by the leading term of the divisor.
Put the answer as the first term in the quotient.
Multiply the answer by the divisor and write it below the like terms of the dividend.
Subtract the product in step 4 from all the terms above it.
Repeat steps 2–5 until reaching the last term of the dividend.
If the remainder is non-zero, express as a fraction using the divisor as the denominator.

Example 5

Divide $5{x}^{2}+3x - 2$ by $x+1$ .

Solution

Set up the division problem. 5x squared divided by x is 5x. Multiply x plus 1 by 5x. Subtract. Bring down the next term. Negative 2x divded by x is negative 2. Multiply x + 1 by negative 2. Subtract.
The quotient is $5x - 2$ . The remainder is 0. We write the result as:

$\dfrac{5{x}^{2}+3x - 2}{x+1}=5x - 2$

Analysis of the Solution

This division problem had a remainder of 0. This tells us that the dividend is divided exactly by the divisor and that, therefore, the divisor and the quotient are factors of the dividend. $5{x}^{2}+3x - 2=\left(x+1\right)\left(5x - 2\right)$

Example 6

Divide $6{x}^{3}+11{x}^{2}-31x+15$ by $3x - 2$ .

Solution

There is a remainder of 1. We can express the result as:

$\dfrac{6{x}^{3}+11{x}^{2}-31x+15}{3x - 2}=2{x}^{2}+5x - 7+\dfrac{1}{3x - 2}$

Analysis of the Solution

We can check our work by using the Division Algorithm to rewrite the solution then multiplying.

$\;\;\;\left(3x - 2\right)\left(2{x}^{2}+5x - 7\right)+1\\=3x\left(2{x}^{2}+5x - 7\right)-2\left(2{x}^{2}+5x - 7\right)+1\\=6x^3+15x^2-21x-4x^2-10x+14+1\\=6{x}^{3}+11{x}^{2}-31x+15$

Notice, as we write our result,

the dividend is $6{x}^{3}+11{x}^{2}-31x+15$
the divisor is $3x - 2$
the quotient is $2{x}^{2}+5x - 7$
the remainder is 1

Try It 4

Divide $16{x}^{3}-12{x}^{2}+20x - 3$ by $4x+5$ .

Show Answer

$\dfrac{16x^3-12x^2+20x-3}{4x+5}=4x^2-8x+15+\left (\dfrac{-78}{4x+5}\right )$

Chapter 3: Polynomial Functions

Learning Outcomes

Dividing a Polynomial by a Monomial

The distributive property

Example 1

Solution

Try It 1

Dividing Polynomials using Long Division

long division revision

The Long Division Algorithm for Arithmetic

Example 2

Solution

Try It 2

The Division Algorithm

division algorithm for polynomials

Example 3

Solution

Try It 3

Example 4

Solution

Answer

using long division to divide polynomials

Example 5

Solution

Analysis of the Solution

Example 6

Solution

Analysis of the Solution

Try It 4

Candela Citations