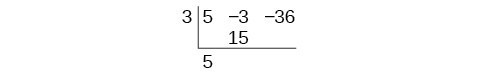Learning Outcomes
- Use synthetic division to divide polynomials by a linear binomial.
Although long division of polynomials will always work, there is a shorthand method for the special case of dividing a polynomial by a linear factor whose leading coefficient is 1. This shorthand method is called synthetic division.
Consider the example of dividing [latex]2{x}^{3}-3{x}^{2}+4x+5[/latex] by [latex]x+2[/latex] using the long division algorithm. Work through the example on your own to make sure you know how to get the solution in figure 1.
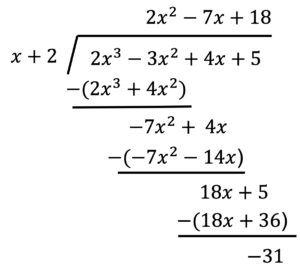
Figure 1. Division of a polynomial by a linear binomial
There is a lot of repetition when we use the division algorithm. If we don’t write the variables but instead line up their coefficients in columns under the division sign and also eliminate some partial products, we already have a simpler version of the entire problem.
Synthetic division takes this simplification further. Collapse the algorithm by moving each of the rows up to fill any vacant spots. Also, instead of multiplying and subtracting the product, we change the sign of the “divisor” to –2, so we can add rather than subtract. The process starts by bringing down the leading coefficient. We then multiply it by the “divisor” and add, repeating this process column by column until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is [latex]2x{^2} -7x+18[/latex] and the remainder is –31.

Figure 3. Synthetic division
synthetic division
Synthetic division is a shortcut that can be used when the divisor is a binomial in the form [latex]x–k[/latex], where [latex]k[/latex] is a constant. In synthetic division, only the coefficients are used in the division process.
- Write [latex]k[/latex] for the divisor.
- Write the coefficients of the dividend written in descending order.
- Bring the leading coefficient down in the first column.
- Multiply the leading coefficient by [latex]k[/latex]. Write the product in the next column.
- Add the terms of the second column.
- Multiply the result by [latex]k[/latex]. Write the product in the next column.
- Repeat steps 5 and 6 for the remaining columns.
- Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on. The degree of the quotient will be one degree less than the degree of the dividend.
There are then two basic rules to synthetic division:
- Add vertically
- Multiply diagonally by [latex]k[/latex]
The process will be made clearer in the examples that follow.
Example 1
Use synthetic division to divide [latex]5x^2-3x-36[/latex] by [latex]x - 3[/latex].
Solution
Begin by setting up the synthetic division. Determine the value of [latex]k[/latex]: [latex]x-3=x-k[/latex], so [latex]k=3[/latex].
Write [latex]k=3[/latex] and the coefficients of the dividend in descending order.
Bring down the leading coefficient. Multiply the leading coefficient 5 by [latex]k=3[/latex] and put the answer under the second column.
Add the numbers vertically in the second column.
Multiply the resulting number by [latex]k=3[/latex] and write the result in the next column: [latex]12\cdot 3=36[/latex].
Then add the numbers vertically in the third column.
The quotient is [latex]5x+12[/latex] with remainder is 0.
[latex]\dfrac{5x^2-3x-36}{x-3}=5x+12[/latex]
With no remainder, [latex]x - 3[/latex] and [latex]5x+12[/latex] are factors of the original polynomial.
[latex]5x^2-3x-36=(x-3)(5x+12)[/latex]
Analysis of the Solution
Just as with long division, we can check our work by multiplying the quotient by the divisor and adding the remainder.
[latex](x - 3)(5x+12)+0\\=x(5x+12)-3(5x+12)\\=5x^2+12x-15x-36\\=5{x}^{2}-3x - 36[/latex]
Example 2
Use synthetic division to divide [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex] by [latex]x+2[/latex].
Solution
The binomial divisor is [latex]x+2=x-(-2)=x-k[/latex], so [latex]k=-2[/latex].
Bring down the leading coefficient. Multiply the leading coefficient 4 by [latex]k=-2[/latex] and put the answer under the second column. Add vertically: 10+(-8) =2. Multiply diagonally by –2: 2(–2) = –4. Repeat until the last column is reached.

The degree of the quotient is always one degree less than the dividend, so we start with an [latex]x^2[/latex] term. The result is [latex]\dfrac{4x^3+10x^2-6x-20}{x+2}=4{x}^{2}+2x - 10[/latex]. The remainder is 0. Thus, [latex]x+2[/latex] and [latex]4x^2+2x-10[/latex] are factors of [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex].
Analysis of the Solution
The graph of the polynomial function [latex]f\left(x\right)=4{x}^{3}+10{x}^{2}-6x - 20[/latex] shows a zero at [latex]x=-2[/latex]. This confirms that [latex]x+2[/latex] is a factor of [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex].

Example 3
Use synthetic division to divide [latex]-9{x}^{4}+10{x}^{3}+7{x}^{2}-6[/latex] by [latex]x - 1[/latex].
Solution
[latex]k=1[/latex]. Notice there is no [latex]x[/latex] term so we must use a zero as the coefficient for that term.
Starting from the first column, add vertically then multiply diagonally by [latex]k=1[/latex].

The result is [latex]\dfrac{-9{x}^{4}+10{x}^{3}+7{x}^{2}-6}{x-1}=-9{x}^{3}+{x}^{2}+8x+8+\frac{2}{x - 1}[/latex].
Try It 1
Use synthetic division to divide [latex]3{x}^{4}+18{x}^{3}-3x+40[/latex] by [latex]x+7[/latex].
TRY IT 2
Try It 3
Use synthetic division to divide the polynomial [latex]3{x}^{3}+14{x}^{2}-23x+6[/latex] by [latex]x+6[/latex].
Candela Citations
- Revision and Adaptation. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- Question ID 29483. Authored by: McClure,Caren. License: Other. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2