3.6: Algebraic Analysis on Intersection Points

Learning Outcomes

Explain the meaning of solving a polynomial equation graphically
Solve polynomial equations using the zero product property
Find the $x$ -intercepts of a polynomial function

The Meaning of Solving a Polynomial Equation

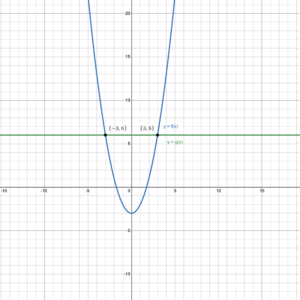
Suppose we have two functions $f(x)=x^2-2x-10$ and $g(x)=5$ . Using Desmos to graph these functions we get the graph in figure 1.

Figure 1. The intersection of two functions

The horizontal line representing $g(x)=5$ intersects the parabola representing $f(x)=x^2-2x-10$ in two points. The two graphs intersect at the points (–3, 5) and (5, 5). These are the points where $f(x)=g(x)$ or, in this case, where $x^2-2x-10=5$ . In other words, the $x$ -coordinates of the intersection points are solutions of the equation $x^2-2x-10=5$ . Finding the intersection points graphically, as in figure 1, is equivalent to solving the equation $f(x)=g(x)$ .

The intersection point(s) between the graphs of any two functions $f(x)$ and $g(x)$ can be found algebraically by setting the two functions equal to each other:

$f(x) = g(x)$

At any intersection point $(x,y)$ , the value of $x$ is the same for both functions, as is the value of $y$ . In other words, $f(x)=g(x)$ means when the two functions have the same input $x$ , and the output of the two functions $f(x)$ and $g(x)$ are equal (i.e., $f(x)=g(x)$ ).

Example 1

Use Desmos to find the solution to the equation $x^2-x-12=0$ .

Solution

Let $f(x)=x^2-x-12$ and $g(x)=0$ . Note that $g(x)=0$ is represented by the $x$ -axis, so we are finding where the graph of $y=f(x)$ intersects the $x$ -axis (i.e., the $x$ -intercepts).

Using Desmos we get:

Intersection of a parabola with the x-axis

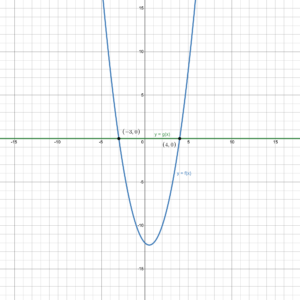
From the graph, $y=f(x)$ intersects the $x$ -axis at (–3, 0) and (4, 0).

So the solution to the equation $x^2-x-12=0$ is $x=–3,\;4$ .

Note. We can always check our solution by substituting the values into the equation:

When $x=–3$ ,

$\begin{aligned}x^2-x-12&=0\\(-3)^2-(-3)-12&=0\\9+3-12&=0\\0&=0\;\;\;\;\text{True}\end{aligned}$

When $x=4$ ,

$\begin{aligned}x^2-x-12&=0\\(4)^2-(4)-12&=0\\16-4-12&=0\\0&=0\;\;\;\;\text{True}\end{aligned}$

Example 2

Use Desmos to find the solution to the equation $x^2-4=-x^2+14$ .

Solution

Let $f(x)=x^2-4$ and $g(x)=-x^2+14$ . then use Desmos to graph the two functions.

Intersection of two functions

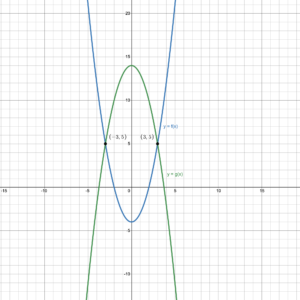
From the graph, the intersection points are (–3, 5) and (3, 5).

So, the solution of the equation $x^2-4=-x^2+14$ is $x=–3,\;3$ .

Try It 1

Use Desmos to find the solution to the equation $x^2-3=6$ .

Show Answer

Intersection of two functions

$x=-3,\;3$

The Relationship of Equivalent Equations, Solutions, Zeros, $x$ -Intercepts, and Points of Intersection

No matter the equation, $f(x)=g(x)$ can always be simplified to $f(x)-g(x)=0$ . The difference in two polynomial functions is always another polynomial function, so solving $f(x)=g(x)$ is equivalent to solving $p(x)=0$ , where $p(x)=f(x)-g(x)$ .

For example, the equation in Example 2, $x^2-4=-x^2+14$ , can be simplified to $2x^2-18=0$ . $x^2-4=-x^2+14$ and $2x^2-18=0$ are equivalent equations so they have identical solutions. Consequently, solving $x^2-4=-x^2+14$ is equivalent to solving $2x^2-18=0$ , which in turn is equivalent to finding the zeros of the function $p(x)=2x^2-18$ . In other words, solving $x^2-4=-x^2+14$ is equivalent to finding the intersection of $p(x)=2x^2-18$ with the $x$ -axis, which is where the $x$ -intercepts lie. Figure 2 shows this graphically.

Intersection of a function and the x-axis

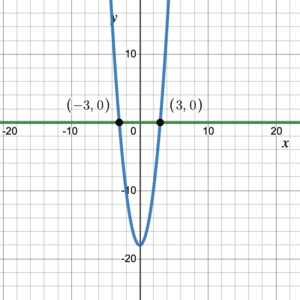
Figure 2. Finding zeros of a function

The zeros of $p(x)=2x^2-18$ are $x=-3,\;3$ .

The $x$ -intercepts of the graph of $p(x)=2x^2-18$ are (–3, 0) and (3, 0).

The graphs of $f(x)=2x^2-18$ and $g(x)=0$ intersect at $x=-3,\;3$ .

The solutions of the polynomial equation $2x^2-18=0$ are $x=-3,\;3$ .

Do you see the relationship between zeros, intersection points, $x$ -intercepts, and solutions?

Example 3

Find the zeros of the polynomial function $f(x)=x^3+2x^2-8x$ .

Solution

Finding the zeros is equivalent to solving the equation $x^3+2x^2-8x=0$ .

Graphically, this is equivalent to finding where the function $f(x)=x^3+2x^2-8x$ intersects the $x$ -axis (the line $g(x)=0$ ).

Using Desmos, we graph $f(x)=x^3+2x^2-8x$ and $g(x)=0$ .

The curve intersects the horizontal line at (–4, 0), (0, 0) and (2, 0).

Consequently, the zeros of $f(x)=x^3+2x^2-8x$ are $x=-4,\;0,\;2$ .

Try It 2

Use Desmos to find the zeros of the polynomial function $f(x)=x^3-2x^2-3x$ .

Show Answer

$x=-1,\;0,\;3$

Solving a Polynomial Equation

We now know what it means to solve a polynomial equation graphically, but what about solving the equation algebraically? Afterall, the intersection points of two curves will not always end up on integer values of $x$ .

One way to solve a polynomial set equal to zero is to use the zero product property.

The Zero Product Property

Suppose we multiply two numbers together and get an answer of zero. What can you say about the two numbers? Could they be $2$ and $5$ ? Could they be $9$ and $–1$ ? No! The only way to get a product of zero, is to multiply by zero. So if a product equals zero, at least one of the factors must be zero. This idea is called the zero product property, and it is useful for solving polynomial equations that can be factored.

Zero Product property

The Zero Product Property states that if the product of two or more factors is $0$ , then at least one of the factors must be $0$ .

If $ab=0$ , then either $a=0$ or $b=0$ , or both $a$ and $b=0$ .

Example 3

Solve the equation $x(x-3)=0$ .

Solution

According to the zero product property,

$x(x-3)=0$ means $x=0$ or $x-3=0$

If $x-3=0$ , then $x=3$ .

Answer

$x=0,\;3$

Example 4

Solve the equation $(2x-5)(7x+6)(3x+4)=0$ .

Solution

$\begin{aligned}(2x-5)(7x+6)(3x+4)&=0\\2x-5=0\;\;\text{ or }\;\;7x+6=0\;\;\text{ or }\;\;3x+4&=0\\2x=5\;\;\;\;\;7x=-6\;\;\;\;\;3x&=-4\\x=\dfrac{5}{2}\;\;\;\;\;x=-\dfrac{6}{7}\;\;\;\;\;x&=-\dfrac{4}{3}\end{aligned}$

Try It 3

Solve the equation:

1. $(x+1)(x-7)=0$

2. $x(3x-5)=0$

3. $-5x(3x+1)(2x-9)=0$

Show Answer

$x=-1,\;7$

$x=0,\;\dfrac{5}{3}$

$x=0,\;-\dfrac{1}{3},\;\dfrac{9}{2}$

Using Factoring to Solve a Polynomial Equation

The zero product property makes it possible for us to solve factored polynomial equations. So, if the equation contains a polynomial that is not factored, the first thing we need to do is 1) simplify it so that it is equal to zero, and 2) factor.

Example 5

Solve the equation $x^2-x-12=0$ .

Solution

The equation is already set equal to zero, so all we have to do is factor it, then use the zero product property to solve it:

$\begin{aligned}x^2-x-12&=0\\(x-4)(x+3)&=0\\x-4=0\;\;\text{or}\;\;x+3&=0\\x=4\;\;\;\;\;\;\;\;\;\;\;\;\;x&=-3\end{aligned}$

Answer

$x=4,\;-3$

Graphically, this means that the graph of the function $f(x)=x^2-x-12$ has $x$ -intercepts at (4, 0) and (–3, 0). See example 1.

The following video shows two more examples of using both factoring and the principle of zero products to solve a polynomial equation.

The next video shows that we can use previously learned methods to factor a trinomial in order to solve a polynomial equation.

What happens if we don’t have zero on one side of the equation? More often than not, we will start by simplifying the equation to get zero on one side.

Example 6

Solve: $s^2-4s=5$

Solution

To solve a polynomial equation, we need to have a zero on one side of the equation so we can factor and use the zero product principle to solve the equation. So, we will start by subtracting 5 from both sides of the equation:

$\begin{aligned}s^2-4s&=5\\s^2-4s-5&=0\\\end{aligned}$

We now have all the terms on the left side and zero on the right side. The polynomial $s^2-4s-5$ factors nicely which makes this equation a good candidate for the zero product principle.

$\begin{aligned}s^2-4s-5&=0\\\left(s+1\right)\left(s-5\right)&=0\end{aligned}$

We separate our factors into two linear equations using the zero product property.

$(s-5)=0$

$s-5=0$

$s=5$

$(s+1)=0$

$s+1=0$

$s=-1$

Therefore, $s=-1\text{ OR }s=5$ .

Try It 4

Solve $15x^2=16x+15$ .

Show Answer

$x=-\dfrac{3}{5},\;\dfrac{5}{3}$

Let’s work through one more example that is similar to the one above, except this example has fractions, yay!

Example 7

Solve $y^2-5=-\dfrac{7}{2}y+\dfrac{5}{2}$ .

Solution

We can solve this equation by first multiplying the equation by a common denominator to get rid of the fractions. Start by multiplying the whole equation by $2$ to eliminate the fractions:

$\begin{aligned}2\left(y^2-5\right)&=2\left(-\dfrac{7}{2}y+\dfrac{5}{2}\right)\\2y^2-10&=-7y+5\end{aligned}$

Now we can move all the terms to one side and see if the resulting polynomial will factor so we can use the zero product property:

$\begin{aligned}2y^2-10&=-7y+5\\2y^2-10+7y-5&=0\\2y^2-15+7y&=0\\2y^2+7y-15&=0\end{aligned}$

We can now check whether this polynomial will factor. Using a table we can list factors until we find two numbers with a product of $ac=2\cdot(-15)=-30$ and a sum of $b=7$ .

Factors of $2\cdot-15=-30$	Sum of Factors
$1,-30$	$-29$
$-1,30$	$29$
$2,-15$	$-13$
$-2,15$	$13$
$3,-10$	$-7$
$-3,10$	$7$

$10,-3$ multiply to –30 and add to 7. We replace $7y$ with $10y-3y$ then factor by grouping:

$\begin{aligned}2y^2+7y-15&=0\\ 2y^2+10y-3y-15&=0\\2y(y+5)-3(y+5)&=0\\(y+5)(2y-3)&=0\end{aligned}$

Now we can set each factor equal to zero and solve:

$\begin{aligned}(2y-3)=0\;\;\;\text{ OR }\;\;\;\left(y+5\right)&=0\\2y=3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y&=-5\\y=\frac{3}{2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y&=-5\end{aligned}$

Remember, we can always check to make sure our solutions are correct:

Check $y=\frac{3}{2}$

$\begin{array}{ccc}\left(\frac{3}{2}\right)^2-5=-\frac{7}{2}\left(\frac{3}{2}\right)+\frac{5}{2}\\\frac{9}{4}-5=-\frac{21}{4}+\frac{5}{2}\\\text{ common denominator = 4}\\\frac{9}{4}-\frac{20}{4}=-\frac{21}{4}+\frac{10}{4}\\-\frac{11}{4}=-\frac{11}{4}\end{array}$

$y=\frac{3}{2}$ is indeed a solution, now check $y=-5$

$\begin{array}{ccc}\left(-5\right)^2-5=-\frac{7}{2}\left(-5\right)+\frac{5}{2}\\25-5=\frac{35}{2}+\frac{5}{2}\\20=\frac{40}{2}\\20=20\end{array}$

$y=-5$ is also a solution, so we must have done something right!

Therefore, $y=\frac{3}{2}\text{ OR }y=-5$ .

The next video shows how to solve another quadratic equation that contains fractions.

Try It 5

Solve $\dfrac{1}{2}x^2+\dfrac{7}{6}x=1$

Show Answer

$x=-3,\;\dfrac{2}{3}$

There are, of course, polynomial equations that do not factor; they are prime. But just because they are prime, does not mean that they do not intersect with the $x$ -axis. For example, the function $f(x)=x^2-3x-1$ is prime, yet it crosses the $x$ -axis at two points. This means that the equation $x^2-3x-1=0$ has two solutions (figure 3). We just can’t find them by factoring.

Parabola rossing the x-axis in two points

Figure 3. A prime polynomial function with two $x$ -intercepts

Figure 4. A prime polynomial function with no $x$ -intercepts

In addition, there are polynomial equations that have no solution. For example the function $g(x)=x^2+2$ never crosses the $x$ -axis, therefore there is no real solution of the equation $x^2+2=0$ (figure 4).

The techniques we have learned can be used to solve polynomial equations that factor, find zeros of functions, find intersection points of functions, and find $x-intercepts$ .

Example 8

Find the $x$ -intercepts of the graph of the function $f(x)=6x^2-11x-10$ .

Solution

We could do this graphically using Desmos, but we end up with fractional $x$ -values. So we will work the problem algebraically.

x-intercepts

$x$ -intercepts are found when $f(x)=0$ so we need to solve the equation $6x^2-11x-10 = 0$

To solve the equation for $x$ we can use factoring and the zero product property:

$\begin{aligned}6x^2-11x-10 &= 0\\(2x-5)(3x+2)&=0\\2x-5=0\;\;\;\;\;\text{or}\;\;\;\;\;3x+2&=0\\x=\dfrac{5}{2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x&=-\dfrac{2}{3}\end{aligned}$

Therefore, the $x$ -intercepts of the function $f(x)=x^2-3x-10$ are $\left(\dfrac{5}{2}, 0\right)$ and $\left(–\dfrac{2}{3}, 0\right)$ .

Example 9

Determine the zeros of the function $f(x)=4x^3-36x$ .

Solution

We need to solve the equation $4x^3-36x=0$ .

We start by factoring then use the zero product property.

There is a common factor of $4x$ : $4x^3-36x=4x(x^2-9)$ .

$x^2-9$ is the difference of two squares $x^2-3^2=(x-3)(x+3)$ .

So,

$\begin{aligned}4x^3-36x&=0\\4x(x-3)(x+3)&=0\\4x=0\;\;\;\text{or}\;\;\;x-3=0\;\;\;\text{or}\;\;\;x+3&=0\\x=0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,x&=-3\end{aligned}$

The zeros of $f(x)=4x^3-36x$ are $x=0,\;3,\;-3$

Try It 6

Find the $x$ -intercepts of the graph of the function $f(x)=15x^3+28x^2-32x$

Show Answer

$\left(-\dfrac{8}{3},0\right)$ , $\left(0,0\right)$ and $\left(\dfrac{4}{5},0\right)$

Try It 7

Solve $(x-2)^2=(x-2)(x+5)$ .

Show Answer

$x=2$

Chapter 3: Polynomial Functions