Learning Objectives
- Define logarithm
- Evaluate logarithms
- Explain “logarithmic growth”
- Define and graph logarithmic functions
- Describe the asymptote of a logarithmic function
- Find the domain and range of an logarithmic function
Definition of a Logarithm
The logarithm of a number [latex]a[/latex], called the argument, with base [latex]b[/latex] is the number [latex]x[/latex] where [latex]b^x=a[/latex]. In other words, a logarithm is the value of the exponent where the given base [latex]b[/latex] to the exponent is equal to the argument [latex]a[/latex]. For example, [latex]\log_{10}{100}=2[/latex], since the given base 10 to the power of 2 is equal to the given number 100. i.e. [latex]10^2=100[/latex]. Also, [latex]\log_{4}{64}=3[/latex], since the given base 4 to the power of 3 is equal to the given number 64. i.e. [latex]4^3=64[/latex].
logarithms
A logarithm is a quantity representing the power to which a fixed number (the base) must be raised to produce a given number.
For all real numbers [latex]x[/latex] and positive real numbers [latex]a[/latex] and [latex]b, b\neq1[/latex],
if [latex]a=b^x[/latex], then [latex]x=\log_b{a}[/latex]
[latex]x=\log_b{a}[/latex] is read ‘[latex]x[/latex] equals the logarithm base [latex]b[/latex] of [latex]a[/latex].
The base of the exponential expression becomes the base of the logarithm.
Notice the restrictions on the numbers [latex]a[/latex] and [latex]b[/latex]. The argument of the logarithm must be positive because the base of the exponent is positive. i.e. [latex]a=\text{positive number}^x=\text{positive number}[/latex]. The base of the logarithm [latex]b[/latex] is positive because it is equal to the base of the exponent, which is positive by definition of exponents (see section 5.1). In addition, [latex]b\neq 1[/latex] because as the base of the exponent, [latex]a=1^x[/latex] means [latex]a[/latex] is always equal to 1, and does not allow for exponential growth (see section 5.1).
Evaluating Logarithms
Some logarithms are easier to evaluate than others. If the argument of the logarithm (the number we are taking the logarithm of) is a power of the base, then evaluating the logarithm is as simple as determining the exponent the base is raised to to get the argument. For example, to determine the value of [latex]\log_7{49}[/latex], we are looking for an exponent, call it [latex]x[/latex], so that [latex]7^x=49[/latex]. Since [latex]7^2=49,\;x=2[/latex]. Consequently, [latex]\log_7{49}=2[/latex].
Example 1
Use the definition of logarithms to determine the value of the logarithm:
- [latex]\log_2{16}[/latex]
- [latex]\log_5{25}[/latex]
- [latex]\log_{10}{10,000}[/latex]
- [latex]\log_3{\frac{1}{81}}[/latex]
- [latex]\log_6{1}[/latex]
Solution
- If [latex]x=\log_2{16}[/latex], then [latex]2^x=16[/latex]. Since [latex]2^4=16,\;x=4[/latex]. Consequently, [latex]\log_2{16}=4[/latex].
- If [latex]x=\log_5{25}[/latex], then [latex]5^x=25[/latex]. Since [latex]5^2=25,\;x=2[/latex]. Consequently, [latex]\log_5{25}=2[/latex].
- If [latex]x=\log_{10}{10,000}[/latex], then [latex]10^x=10,000[/latex]. Since [latex]10^4=10,000,\;x=4[/latex]. Consequently, [latex]\log_{10}{10,000}=4[/latex].
- If [latex]x=\log_3{\frac{1}{81}}[/latex], then [latex]3^x=\frac{1}{81}[/latex]. Since [latex]3^4=81,\;3^{-4}=\frac{1}{81}[/latex], and [latex]x=-4[/latex]. Consequently, [latex]\log_3{\frac{1}{81}}=-4[/latex].
- If [latex]x=\log_6{1}[/latex], then [latex]6^x=1[/latex]. Since [latex]6^0=1,\;x=0[/latex]. Consequently, [latex]log_6{1}=0[/latex].
Try It 1
Use the definition of logarithms to determine the value of the logarithm:
- [latex]\log_3{27}[/latex]
- [latex]\log_2{32}[/latex]
- [latex]\log_{10}{1,000,000}[/latex]
- [latex]\log_4{\frac{1}{16}}[/latex]
- [latex]\log_{17}{1}[/latex]
Show Answer
- [latex]\log_3{27}=3[/latex]
- [latex]\log_2{32}=5[/latex]
- [latex]\log_{10}{1,000,000}=6[/latex]
- [latex]\log_4{\frac{1}{16}}=-2[/latex]
- [latex]\log_{17}{1}=0[/latex]
Did you notice that in example 1, [latex]\log_6{1}=0[/latex], and in try it 1, [latex]\log_{17}{1}=0[/latex]? In fact, [latex]\log_{b}{1}=0[/latex] for any [latex]b>0,\;b\neq1[/latex]. Why? Because [latex]b^0=1[/latex] is true for all values of [latex]b\neq0[/latex].
logarithm property
Since [latex]b^0=1[/latex] for all values of [latex]b\neq0[/latex],
[latex]\log_b{1}=0[/latex]
When the argument of the logarithm is not a power of the base, it is not as obvious what the exponent is. For example, to determine the value of [latex]log_2{5}[/latex], we need to find a value [latex]x[/latex] such that [latex]2^x=5[/latex]. We know that [latex]2^2=4[/latex] and [latex]2^3=8[/latex]. So since [latex]5[/latex] lies between 4 and 8, [latex]x[/latex] must lie between 2 and 3. i.e. [latex]2<\log_2{5}<3[/latex]. We could use a calculator to help us get closer to the value, using trial and error:
We know that [latex]25[/latex]. Still too large, but now we know that [latex]25[/latex], so 2.4 is too large. Now we know that [latex]2.1
Example 2
Write an equivalent logarithmic equation to solve for [latex]x[/latex]:
- [latex]4^x=8[/latex]
- [latex]5^x=9[/latex]
- [latex]7^{x+1}=4[/latex]
- [latex]3^{2x}=12[/latex]
- [latex]2^{3x-5}=20[/latex]
Solution
We write an equivalent logarithmic equation, [latex]b^x=a\Longleftrightarrow x=log_ba[/latex], then solve for [latex]x[/latex]:
|
Solutions
|
Solutions
|
|
1.
[latex]\begin{aligned}4^x&=8\\x&=\log_4{8}\end{aligned}[/latex]
|
2.
[latex]\begin{aligned}5^x&=9\\x&=\log_5{9}\end{aligned}[/latex]
|
|
3.
[latex]\begin{aligned}7^{x+1}&=4\\x+1&=\log_7{4}\\x&=\log_7{4}-1\end{aligned}[/latex]
|
4.
[latex]\begin{aligned}3^{2x}&=12\\2x&=\log_3{12}\\x&=\frac{1}{2}\log_3{12}\end{aligned}[/latex]
|
| 5.
[latex]\begin{aligned}2^{3x-5}&=20\\3x-5&=log_2{20}\\3x&=\log_2{20}+5\\x&=\dfrac{\log_2{20}+5}{3}\end{aligned}[/latex]
|
|
Try It 2
Write an equivalent logarithmic equation to solve for [latex]x[/latex]:
- [latex]4^x=3[/latex]
- [latex]5^x=6[/latex]
- [latex]7^{x-2}=9[/latex]
- [latex]3^{4x}=10[/latex]
- [latex]2^{2x+7}=30[/latex]
Show Answer
- [latex]x=\log_4{3}[/latex]
- [latex]x=\log_5{6}[/latex]
- [latex]x=\log_7{9}+2[/latex]
- [latex]x=\frac{1}{4}\log_{3}{10}[/latex]
- [latex]x=\dfrac{\log_2{30}-7}{2}[/latex]
Logarithmic Growth
Unlike exponential growth that increases fast by multiplying by a constant each time, logarithmic growth increases very slowly. For example, the table 1 shows logarithmic growth with base 2. Notice that the value of the logarithm increases by only 1 as the value of the input (i.e., [latex]x[/latex]) doubles each time.
| [latex]x[/latex] |
[latex]log_2{x}[/latex] |
| [latex]\dfrac{1}{8}[/latex] |
[latex]-3[/latex] |
| [latex]\dfrac{1}{4}[/latex] |
[latex]-2[/latex] |
| [latex]\dfrac{1}{2}[/latex] |
[latex]-1[/latex] |
| [latex]1[/latex] |
[latex]0[/latex] |
| [latex]2[/latex] |
[latex]1[/latex] |
| [latex]4[/latex] |
[latex]2[/latex] |
| [latex]8[/latex] |
[latex]3[/latex] |
| [latex]16[/latex] |
[latex]4[/latex] |
| [latex]32[/latex] |
[latex]5[/latex] |
| [latex]64[/latex] |
[latex]6[/latex] |
| [latex]128[/latex] |
[latex]7[/latex] |
| Table 1. Logarithmic growth |
Try It 3
Create a table showing logarithmic growth base 3. Comment on any patterns you see.
Show Answer
| [latex]x[/latex] |
[latex]\log_3{x}[/latex] |
| [latex]\frac{1}{27}[/latex] |
[latex]-3[/latex] |
| [latex]\frac{1}{9}[/latex] |
[latex]-2[/latex] |
| [latex]\frac{1}{3}[/latex] |
[latex]-1[/latex] |
| [latex]1[/latex] |
[latex]0[/latex] |
| [latex]3[/latex] |
[latex]1[/latex] |
| [latex]9[/latex] |
[latex]2[/latex] |
| [latex]27[/latex] |
[latex]3[/latex] |
| [latex]81[/latex] |
[latex]4[/latex] |
| [latex]243[/latex] |
[latex]5[/latex] |
[latex]\log_3{x}[/latex] only increases by 1 as [latex]x[/latex] increases by a factor of 3
Logarithmic Functions and their Graphs
A logarithmic function has the form [latex]f(x) = \log_b{x}[/latex], where [latex]b[/latex] is a positive real number and [latex]b \neq 1[/latex]. But why is [latex]b>0[/latex] and [latex]b\neq1[/latex]? The base of the logarithm [latex]b[/latex] is positive because it is equal to the base of the exponent, which is positive by the definition of exponential functions (see section 5.1). If [latex]b = 1[/latex], the corresponding exponential equation of [latex]\log_1a=x[/latex] is [latex]1^x=a[/latex]. But [latex]1^x=1[/latex] for all values of [latex]x[/latex], so cannot equal [latex]a[/latex]. Hence [latex]b\neq1[/latex].
In addition, the graph of [latex]y=\log_1{x}[/latex] is the vertical line [latex]x=1[/latex] when [latex]b=1[/latex]. This is because the equivalent exponential equation is [latex]x=1^y[/latex] and since [latex]1^y=1[/latex] for all values of [latex]y[/latex], [latex]x=1[/latex], which is a vertical line and not a function.
Logarithmic function
The logarithmic function [latex]f(x)=\log_bx[/latex] is defined as the inverse of the exponential function [latex]g(x)=b^x[/latex], where [latex]b>0[/latex] and [latex]b\neq1[/latex].
Graphing a Logarithmic Function
To graph a logarithmic function, we can create a table of values, transfer them to the coordinate plane, and then connect the points with a curve. Figure 1 shows the graph of the logarithmic function [latex]f(x)=\log_2{x}[/latex] based on table 1.

Figure 1. The graph of the function [latex]f(x)=\log_2{x}[/latex].
The Vertical Asymptote and Intercepts
Notice that the graph (figure 1) is always increasing and passes through the point (1, 0) since [latex]\log_b{1}=0[/latex]. The point (1, 0) is the [latex]x[/latex]-intercept of the graph of any logarithmic function in the form [latex]f(x)=\log_b{x}[/latex] with [latex]b>0,\;b\neq1[/latex].
Notice also that the graph has no [latex]y[/latex]-intercept because the graph never touches the [latex]y[/latex]-axis. This is due to the graphs significant feature; a vertical asymptote, [latex]x=0[/latex]. i.,e. the [latex]y[/latex]-axis. As [latex]x[/latex] gets closer and closer to zero, the graph approaches the [latex]y[/latex]-axis as it moves quickly towards negative infinity on the [latex]y[/latex]-axis. Vertical asymptotes can never be crossed. Table 2 shows that as [latex]x[/latex] gets closer and closer to zero, the value of [latex]f(x)=\log_2{x}[/latex] gets more and more negative.
| [latex]x[/latex] |
[latex]f(x)=\log_2x[/latex] |
| [latex]2^{-1}[/latex] |
[latex]-1[/latex] |
| [latex]2^{-10}[/latex] |
[latex]-10[/latex] |
| [latex]2^{-100}[/latex] |
[latex]-100[/latex] |
| [latex]2^{-1000}[/latex] |
[latex]-1000[/latex] |
| [latex]2^{-10,000}[/latex] |
[latex]-10,000[/latex] |
| [latex]2^{-100,000}[/latex] |
[latex]-100,000[/latex] |
| [latex]2^{-1,000,000}[/latex] |
[latex]-1,000,000[/latex] |
| Table 2. As [latex]x[/latex] gets closer to zero, [latex]f(x)[/latex] heads towards negative infinity |
As the the value of [latex]x[/latex] gets close to zero, the value of the function [latex]y[/latex] goes to negative infinity. The value of [latex]x[/latex] may be closer and closer to zero but will never be zero because the answer for the logarithm [latex]\log_2{0}[/latex] does not exist; we are not able to find the value [latex]y[/latex] such that [latex]2^y=0[/latex]. The [latex]y[/latex]-axis, therefore, is the vertical asymptote of the function [latex]f(x)=\log_2{x}[/latex].
The graph in Figure 2 illustrates the logarithmic function [latex]f(x)=\log_{2}{(x+8)}[/latex], which has an [latex]x[/latex]-intercept (-7, 0) because [latex]g(-7)=\log_{2}{(-7+8)=\log_2{1}=0}[/latex]. The [latex]y[/latex]-intercept is (0, 3) because [latex]g(0)=\log_{2}{(0+8)}=\log_2{8}=3[/latex]. Its vertical asymptote is [latex]x = -8[/latex] because the graph approaches but never meets the vertical line [latex]x = -8[/latex]. The value of the function does not exist when [latex]x=-8.[/latex] We will discuss vertical asymptotes for transformed logarithmic functions in the next section.

Figure 2. The graph of the function [latex]f(x)=\log_2{(x+8)}[/latex].
Domain and Range
The range of any logarithmic function in the form [latex]f(x)=\log_bx[/latex] is all real numbers, or {[latex]x | x \in \mathbb{R}[/latex]}. The domain of any logarithmic function in the form [latex]f(x)=\log_bx[/latex] is all real numbers that are greater than zero.
We will discuss the domain and range of transformed logarithmic functions later. However, figure 2 shows that the domain of [latex]f(x)=\log_2{(x+8)}[/latex] is [latex](-8,\;+\infty)[/latex]. The vertical asymptote plays an important role in determining the domain of a logarithmic function.
Try It 4
Use the table of values you created in Try It 3 to graph [latex]f(x)=\log_3x[/latex]. State the domain and the range, the [latex]x[/latex]-intercept, and the vertical asymptote.
Show Answer
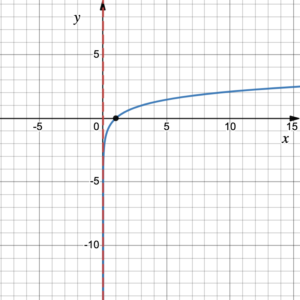
The graph of the function [latex]f(x)=\log_3{x}[/latex].
Domain = [latex](0,\;+\infty)[/latex]Range = [latex](-\infty,\;+\infty)[/latex][latex]x[/latex]-intercept = (1, 0)
vertical asymptote is the line [latex]x=0[/latex]
Candela Citations
CC licensed content, Original
- Logarithmic Functions and Their Graphs. Authored by: Leo Chang and Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Leo Chang and Hazel McKenna. Provided by: Utah Valley University. Located at: http://www.desmos.com/calculator. License: CC BY: Attribution
- All examples and Try Its: hjm192; hjm794; hjm001; hjm085. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution



