- Graph the inverse function of a logarithmic function
- Find the equation of the inverse function of a logarithmic function
- Use compositions of function to show equivalency: [latex]f\left(f^{-1}(x)\right)=f^{-1}\left(f^(x)\right)=x[/latex]
Graphing the Inverse Function
One way to graph the inverse of a logarithmic function is by creating and using its inverse table. For example, to graph the inverse function of [latex]f(x)=log_2{x}[/latex], we start by creating a table of values for the function (Table 1).
| [latex]x[/latex] | [latex]y=\log_2{x}[/latex] |
| [latex]\dfrac{1}{8}[/latex] | [latex]-3[/latex] |
| [latex]\dfrac{1}{4}[/latex] | [latex]-2[/latex] |
| [latex]\dfrac{1}{2}[/latex] | [latex]-1[/latex] |
| [latex]1[/latex] | [latex]0[/latex] |
| [latex]2[/latex] | [latex]1[/latex] |
| [latex]4[/latex] | [latex]2[/latex] |
| [latex]8[/latex] | [latex]3[/latex] |
| Table 1. Table of values for [latex]f(x)=\log_2{x}[/latex] | |
To create an inverse table, we switch the values in the [latex]x[/latex] and [latex]y[/latex] columns so that the inputs become the values of [latex]y[/latex] and the outputs become the values of [latex]x[/latex]. The table after switching the values of the [latex]x[/latex] and [latex]y[/latex] columns is the inverse table (Table 2). Since [latex]f(x)=\log_2{x}[/latex] is a one-to-one function, its inverse will also be a one-to-one function.
| [latex]x[/latex] | [latex]y=f^{-1}(x)[/latex] |
| [latex]-3[/latex] | [latex]\dfrac{1}{8}[/latex] |
| [latex]-2[/latex] | [latex]\dfrac{1}{4}[/latex] |
| [latex]-1[/latex] | [latex]\dfrac{1}{2}[/latex] |
| [latex]0[/latex] | [latex]1[/latex] |
| [latex]1[/latex] | [latex]2[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]8[/latex] |
| Table 2. Inverse table | |
Looking at the values in table 2, notice that as [latex]x[/latex] increases by 1, the inverse function value increases by a multiple of 2. This means that the inverse of a logarithmic function is an exponential function. In this case, the inverse of [latex]f(x)=\log_2{x}[/latex] is [latex]f^{-1}(x)=2^x[/latex].
Figure 1 shows the graphs of the function [latex]f(x)=\log_2{x}[/latex] (the blue curve) and its inverse (the green curve) graphed usings the values in Tables 1 and 2. Notice that the graph of the inverse function is a reflection of the graph of the original function with respect to the line [latex]y=x[/latex] (the red line).
Figure 1. The graphs of the function [latex]f(x)=\log_2{x}[/latex] and its inverse function.
Notice that the inverse is also a function because it passes the vertical line test. The inverse is a one-to-one mapping. Therefore, the inverse is a function.
Example 1
Use Desmos to graph [latex]f(x)=2\log_2{(x-3)}+1[/latex], then use reflection to graph its inverse function.
Solution
Copying and pasting the function into Desmos yields:
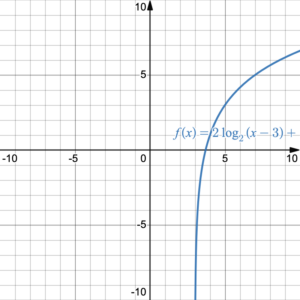
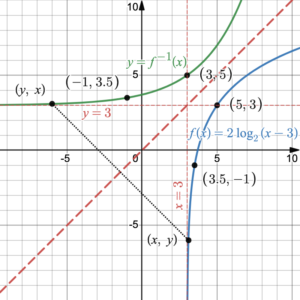
Now we draw in the line [latex]y=x[/latex] and reflect every point on the graph of [latex]y=f(x)[/latex] across the line [latex]y=x[/latex] to get the inverse. Every point [latex](x,\;y)[/latex] is reflected to [latex](y,\;x)[/latex]. The vertical asymptote [latex]x=3[/latex] reflects to a horizontal asymptote [latex]y=3[/latex].
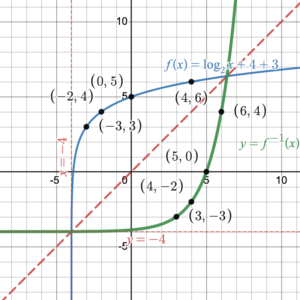
Try It 1
Use Desmos to graph [latex]f(x)=\log_2{(x+4)}+3[/latex], then use reflection to graph its inverse function.
The Inverse Function Equation
We already know that to find the equation of an inverse function for a given function, we set [latex]y=f(x)[/latex], switch [latex]x[/latex] and [latex]y[/latex], then solve for [latex]y[/latex]. For example, given the logarithmic function [latex]f(x)=\log_2{x}[/latex], we first set [latex]y=f(x)[/latex]:
[latex]y=\log_2{x}[/latex]
Then we switch [latex]x[/latex] and [latex]y[/latex] to get the inverse:
[latex]x=\log_2y[/latex]
Now we solve for [latex]y[/latex] by writing this logarithmic equation as an equivalent exponential equation. Based on the definition of logarithm, the base of the logarithm, 2, becomes the base of the exponential:
[latex]y=2^x[/latex]
Therefore, the inverse function of the logarithmic function [latex]f(x)=\log_2{x}[/latex] is:
[latex]f^{-1}(x)=2^{x}[/latex]
Example 2
Determine the inverse function of [latex]g(x)=\log_5x[/latex].
Solution
First set [latex]y=g(x)[/latex]: [latex]y=\log_5x[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse: [latex]x=\log_5y[/latex]
Use the definition of logarithm to solve for [latex]y[/latex]: [latex]y=5^x[/latex]
Write in function notation: [latex]g^{-1}(x)=5^x[/latex]
Try It 2
Determine the inverse function of [latex]h(x)=\log_7x[/latex].
Example 3
Determine the inverse function of the logarithmic function [latex]f(x)=\log_4{(x+5)}[/latex].
Solution
First set [latex]y=f(x)[/latex]: [latex]y=\log_4{(x+5)}[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse: [latex]x=\log_4{(y+5)}[/latex]
Use the definition of logarithm to solve for [latex]y[/latex]: [latex]y+5=4^x[/latex]
Solve for [latex]y[/latex] by subtracting 5 from both sides: [latex]y=4^x-5[/latex]
Write in function notation: [latex]f^{-1}(x)=4^x-5[/latex]
Try It 3
Determine the inverse function of the logarithmic function [latex]g(x)=\log_3{(x-6)}[/latex].
For a logarithmic function that is in the form [latex]f(x)=a\log_b{x-h}+k[/latex], we must first isolate the logarithm, before using the definition of a logarithm to solve for [latex]y[/latex].
Example 4
Determine the inverse function of the logarithmic function [latex]f(x)=4\log_3{(x+2)}[/latex].
Solution
First set [latex]y=f(x)[/latex]:[latex]y=4\log_3{(x+2)}[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse: [latex]x=4\log_3{(y+2)}[/latex]
Isolate the logarithm by dividing both sides by 4: [latex]\frac{1}{4}x=\log_3{(y+2)}[/latex]
Use the definition of logarithm to solve for [latex]y[/latex]: [latex]y+2=3^{\frac{x}{4}}[/latex]
Solve for [latex]y[/latex] by subtracting 2 from both sides: [latex]y=3^{\frac{x}{4}}-2[/latex]
Write in function notation: [latex]f^{-1}(x)=3^{\frac{x}{4}}-2[/latex]
Try It 4
Determine the inverse function of the logarithmic function [latex]f(x)=5\log_7{(x-3)}[/latex].
Example 5
Determine the inverse function of the logarithmic function [latex]f(x)=\log_5{(x-3)}+2[/latex].
Solution
First set [latex]y=f(x)[/latex]: [latex]y=\log_5{(x-3)}+2[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse: [latex]x=\log_5{(y-3)}+2[/latex]
Isolate the logarithm by subtracting 2 from both sides: [latex]x-2=\log_5{(y-3)}[/latex]
Use the definition of logarithm to solve for [latex]y[/latex]: [latex]y-3=5^{x-2}[/latex]
Solve for [latex]y[/latex] by adding 3 to both sides: [latex]y=5^{x-2}+3[/latex]
Write in function notation: [latex]f^{-1}(x)=5^{x-2}+3[/latex]
Example 6
Determine the inverse function of the logarithmic function [latex]f(x)=\dfrac{2}{5}\log_3{(8x)}-4[/latex].
Solution
First set [latex]y=f(x)[/latex]: [latex]y=\dfrac{2}{5}\log_3{(8x)}-4[/latex]
Switch [latex]x[/latex] and [latex]y[/latex] to get the inverse: [latex]x=\dfrac{2}{5}\log_3{(8y)}-4[/latex]
Isolate the logarithm by adding 4 to both sides: [latex]x+4=\dfrac{2}{5}\log_3{(8y)}[/latex]
Isolate the logarithm by multiplying both sides by [latex]\dfrac{5}{2}[/latex]: [latex]\dfrac{5}{2}(x+4)=\log_3{(8y)}[/latex]
Use the definition of logarithm to solve for [latex]y[/latex]: [latex]8y=3^{\frac{5}{2}(x+4)}[/latex]
Solve for [latex]y[/latex] by dividing both sides by 8: [latex]y=\frac{1}{8}\cdot3^{\frac{5}{2}(x+4)}[/latex]
Write in function notation: [latex]f^{-1}(x)=\frac{1}{8}\cdot3^{\frac{5}{2}(x+4)}[/latex]
Try It 5
Determine the inverse function of the logarithmic function:
- [latex]f(x)=\log_2{(x-9)}+1[/latex]
- [latex]g(x)=\dfrac{3}{4}\log_5{x}-2[/latex]
- [latex]h(x)=\dfrac{1}{3}\log_2{(x+5)}+8[/latex]
- [latex]F(x)=6\log_{10}{(x-3)}+6[/latex]
Composition of Inverse Functions
It is important to remember that an inverse function ‘undoes’ what was ‘done’ by the original function. Logarithmic functions and inverse functions are inverses of one another, so if we apply one function then apply its inverse, we should get back to where we started.
Consider the function [latex]f(x)=\log_4x[/latex] and its inverse function [latex]f^{-1}(x)=4^x[/latex]. Now let’s perform a composition of functions:
[latex]\begin{aligned}\left(f\circ f^{-1}\right)(x)&=f\left(f^{-1}(x)\right)\\&=f\left(4^x\right)\\&=\log_4{4^x}\end{aligned}[/latex]
To simplify [latex]\log_4{4^x}[/latex], let’s set [latex]a=\log_4{4^x}[/latex]. Then using the definition of logarithms, we can write an equivalent exponential equation:
[latex]4^a=4^x[/latex]
Since the bases are identical, the exponents must be equal:
[latex]a=x[/latex]
Consequently, [latex]\log_4{4^x}=x[/latex] and, therefore, [latex]\left(f\circ f^{-1}\right)(x)=x[/latex].
If we perform the composition in the opposite direction we get:
[latex]\begin{aligned}\left(f^{-1}\circ f\right)(x)&=f^{-1}\left(f(x)\right)\\&=f^{-1}\left(\log_4x\right)\\&=4^{\log_4x}\end{aligned}[/latex]
To simplify [latex]4^{\log_4x}[/latex], let’s set [latex]a=4^{\log_4x}[/latex]. Then using the definition of logarithms, we can write an equivalent exponential equation:
[latex]\log_4a=\log_4x[/latex]
Since logarithms are one-to-one functions, [latex]a=x[/latex].
Consequently, [latex]4^{\log_4x}=x[/latex] and, therefore, [latex]\left(f^{-1}\circ f\right)(x)=x[/latex].
Example 7
Use composition of functions to show that [latex]f(x)=\log_2{(x+1)}[/latex] and [latex]g(x)=2^x-1[/latex] are inverse functions.
Solution
It doesn’t matter the order in which we compose the functions.
[latex]\begin{aligned}\left(f\circ g\right)(x)&=f\left(2^x-1\right)\\&=\log_2{(2^x-1+1)}\\&=\log_2{2^x}\end{aligned}[/latex]
To simplify [latex]\log_2{2^x}[/latex], let [latex]a=\log_2{2^x}[/latex], then using the definition of logarithms:
[latex]\begin{aligned}2^a&=2^x\\a&=x\end{aligned}[/latex]
Consequently, [latex]\left(f\circ g\right)(x)=x[/latex]
[latex]\begin{aligned}\left(g\circ f\right)(x)&=g\left(\log_2{(x+1)}\right)\\&=2^{\log_2{(x+1)}}-1\end{aligned}[/latex]
To simplify [latex]2^{\log_2{(x+1)}}[/latex], let [latex]a=2^{\log_2{(x+1)}}[/latex], then using the definition of logarithms:
[latex]\log_2{a}=\log_2{(x+1)}[/latex]
[latex]a=x+1[/latex]
Hence,
[latex]\begin{aligned}\left(g\circ f\right)(x)&=g\left(\log_2{(x+1)}\right)\\&=2^{\log_2{(x+1)}}-1\\&=(x+1)-1\\&=x\end{aligned}[/latex]
Consequently, [latex]\left(g\circ f\right)(x)=x[/latex]
Therefore, [latex]f(x)=\log_2{(x+1)}[/latex] and [latex]g(x)=2^x-1[/latex] are inverse functions.
Try It 6
Use composition of functions to show that [latex]f(x)=\log_3{(x+4)}[/latex] and [latex]g(x)=3^x-4[/latex] are inverse functions.
