6.5: Algebraic Analysis on Intersection Points

Learning Objectives

Describe the meaning of solving a logarithmic equation
Solve logarithmic equations using the rules for logarithms
Solve exponential equations using logarithms

The Meaning of Solving Logarithmic Equations

Intersection point of functions

In chapter 3, we learned that the meaning of solving an equation is to find the intersection point(s) between two functions. The intersection point(s) between the graphs of any two functions $f(x)$ and $g(x)$ can be found algebraically by setting the two functions equal to each other:

$f(x)=g(x)$

When the functions are equal, the value of $x$ is the same for both functions, as is the function value. In other words, $f(x)=g(x)$ means that the two functions have the same input $x$ as well as the same output (i.e $f(x)=g(x)$ ). For example, solving the equation $\log_2{(x+1)} +\log_2{4}=3$ means finding the intersection point between the two functions $f(x)=\log_2{(x+1)} +\log_2{4}$ and $g(x)=3$ (figure 1).

Figure 1. The intersection between two functions at the point $(1, 3)$ .

Finding the $x$ -value given a function value

Given the equation $\log_2{(x+1)} +\log_2{4}=3$ , in addition to the interpretation of finding the intersection point between the two functions $f(x)=\log_2{(x+1)} +\log_2{4}$ and $g(x)=3$ , another interpretation of the equation is finding the $x$ value when the function value of $f(x)=\log_2{(x+1)} +\log_2{4}$ is $3$ (figure 2).

Figure 2. Find the $x$ coordinate given the $y$ coordinate is 3.

Graphically, this means finding the $x$ value as a given $y$ -value on a graph, then moving vertically down to the $x$ -axis to determine the corresponding $x$ -value. In figure 2, to solve $\log_2{(x+1)} +\log_2{4}=3$ , we graph the function $f(x)=\log_2{(x+1)} +\log_2{4}$ , look for 3 on the $y$ -axis then determine which $x$ -value has a function value at 3. In this case, $x=1$ .

Solving an equation in one variable

Algebraically, $\log_2{(x+1)} +\log_2{4}=3$ is an equation in one variable. When solving an equation in one variable, we find the value of the variable that satisfies the equation (e.g., the $x$ -value). There is no function value to report as the equation is in just one variable.

For example, when solving the equation, $\log_2{(x+1)} +\log_2{4}=3$ , we find the value of $x$ that makes the equation true. The value of $x$ is 1 because $\log_2{(1+1)} +\log_2{4}=1+2=3$ . We need algebraic methods to solve logarithmic equations, including the properties of equality covered in chapter 3.

In summary, when we set functions equal to each other, we are finding the intersection point between two functions (e.g., $f(x)=\log_2{(x+1)} +\log_2{4}$ and $g(x)=3$ ). In this example, the intersection point between the graphs of the two functions $f(x)=\log_2{(x+1)} +\log_2{4}$ and $g(x)$ is $(1, 3)$ because the $y$ -value is the function value $f(1)=\log_2{(1+1)} +\log_2{4}=\log_2{2}+\log_2{2^2}=1+2=3$ and $g(x)=3$ . However, when we are solving an equation algebraically, there is no function in sight so we can just report the value of the variable (e.g., $x$ ).

Solving Logarithmic Equations Using the Rules for Logarithms

When solving a logarithmic equation that involves more than one logarithm (e.g., $\log_2{(x-2)}+\log_2{x}=3$ ), we may be able to combine the logarithms, if they have the same base, into a single logarithm using the properties of logarithms we learned in the last section, and then we can use the definition of logarithm to turn the single logarithm into an exponential equation, which we can solve.

Example 1

Solve $\log_2{(x-2)}+\log_2{x}=3$ .

Solution

$\begin{aligned}\log_2{(x-2)}+\log_2{x}&=3\\\\\log_2{x(x-2)}&=3\\\\x(x-2)&=2^3\\\\x^2-2x&=8\\\\x^2-2x-8&=0\\\\(x-4)(x+2)&=0\\\\x=4\text{ or }x&=-2\end{aligned}$

However, we must check our solutions because the argument of all logarithms must be positive:

The arguments in the original equation are $x-2$ and $x$ .

For $x-2$ to be positive $x>2$ , and for $x$ to be positive $x>0$ .

To satisfy both arguments $x>2$ .

This means that the solution $x=4$ is our only answer, since $-2<2$ and $\log_2{-2}$ does not exist.

Answer

$x=4$

Example 2

Solve $5\ln3x+2=7$ .

Solution

$\begin{aligned}5\ln3x+2&=7\\\\5\ln3x&=5\\\\\dfrac{5\ln3x}{5}&=\dfrac{5}{5}\\\\\ln3x&=1\\\\3x&=e^1\\\\x=\dfrac{e}{3}\end{aligned}$

The argument in the original equation is $3x$ which is positive when $x>0$ . $\dfrac{e}{3}>0$ so we have the solution.

Answer

$x=\dfrac{e}{3}$

Example 3

Solve $\ln16x+\ln{x}=4$ .

Solution

$\begin{aligned}\ln{16x}+\ln{x}&=4\\\\\ln{x(16x)}&=4\\\\\ln{(16x^2)}&=4\\\\16x^2&=e^4\\\\x^2&=\dfrac{e^4}{16}\\\\x&=\pm\sqrt{\dfrac{e^4}{16}}\\x&=\pm\dfrac{e^2}{4}\end{aligned}$

The arguments in the original equation are $x$ and $16x$ that must be positive, so we must ensure that $x>0$ .

Therefore, we cannot use the negative radical and $x=\dfrac{e^2}{4}$ .

Try It 1

Solve $\log_6{(x-5)}+\log_6{x}=1$ .

Show Answer

x = 6

$x=6$

Try It 2

Solve $7\ln3x-4=3$ .

Show Answer

x = \frac{e}{3}

$x=\dfrac{e}{3}$

Try It 3

Solve $\log18x+\log{2x}=4$ .

Show Answer

x = \frac{50}{3}

$x=\dfrac {50}{3}$

In Try It 3, remember that graphically we are finding the point of intersection between the functions $f(x)=\log18x+\log{2x}$ and $g(x)=4$ (figure 3). Looking at the graph is a great way to check your solution.

Figure 3. Intersection of two functions

Solving Exponential Equations Using Logarithms

We have already seen how to solve exponential equations in the form $b^x=a$ by writing an equivalent logarithmic equation $x=\log_b{a}$ . We can also use logarithms and rules for logarithms to solve exponential equations. Since an exponential equation has the variable in the exponent, we can take logarithms with any positive base (except for 1) on both sides of the equation, use the power rule for logarithms to pull the exponent in front of the logarithm, and then solve the resulting equation for the variable (e.g., $x$ ).

For example, to solve the equation $3^{2x}=5.4$ , we can start by taking the base 3 logarithm of both sides of the equation:

$\log_3{3^{2x}}=\log_3{5.4}$

Then we can pull the exponent in front of the logarithm:

$2x\log_3{3}=\log_3{5.4}$

$\log_3{3}=1$ and we are left with a linear equation that we know how to solve:

$\begin{aligned}2x&=\log_3{5.4}\\x&=\dfrac{1}{2}\log_3{5.4}\end{aligned}$

If we want a decimal answer, we can convert $\log_3{5.4}$ into base 10 or base $e$ using the change of base formula:

$\log_3{5.4}=\dfrac{\ln{5.4}}{\ln3}=1.535...$

Then the solution is:

$\begin{aligned}x&=\dfrac{1}{2}\log_3{5.4}\\&= \dfrac{1}{2}\times(1.5350...)\\&\approx 0.7675\end{aligned}$

Remember to complete all calculations on the calculator before rounding the answer.

When solving this example, we used base 3 when taking the logarithm of both sides of the equation. In fact, we could choose any (valid) base. The reason we choose base 3 is because $\log_3{3}$ is equal to 1, which helps to simplify the equation.

Here is the same equation, but this time we will take the natural logarithm of both sides:

$\begin{aligned}3^{2x}&=5.4\\\\ \ln{3^{2x}}&=\ln{5.4}\\\\2x\ln{3}&=\ln{5.4}\\\\x&=\dfrac{\ln{5.4}}{2\ln{3}}\\\\x&\approx 0.7675\end{aligned}$

This is exactly the same answer we had before but this time there is no need to change the base to get a decimal answer since most calculators have a natural logarithm button.

Example 4

Solve the equation $4e^{3x}e=10$ .

Solution

$\begin{aligned}4e^{3x}e&=10\\\\4e^{3x+1}&=10&&\text{Simplify }e^{3x}e^1=e^{3x+1}\\\\\dfrac{4e^{3x+1}}{4}&=\dfrac{10}{4}&&\text{Divide both side by 4}\\\\e^{3x+1}&=\dfrac{5}{2}&&\text{Simplify the fraction}\\\\\ln{e^{3x+1}}&=\ln{\dfrac{5}{2}}&&\text{Take the natural logarithm of both sides}\\\\(3x+1)\ln{e}&=\ln{\dfrac{5}{2}}&&\text{Pull the exponent in front of the logarithm}\\\\(3x+1)\times1 &=\ln{\dfrac{5}{2}}&&\text{Evaluate }\ln{e}=1\\\\(3x+1)&=\ln{\dfrac{5}{2}}&&\text{Simplify}\\\\3x&=\ln{\dfrac{5}{2}}-1&&\text{Subtract 1 from both sides}\\\\ \dfrac{3x}{3}&=\dfrac{1}{3}\left(\ln{\dfrac{5}{2}-1}\right)&&\text{Divide both sides by 3}\\\\x&=\dfrac{1}{3}\ln{\dfrac{5}{2}}-\dfrac{1}{3}&&\text{Distribute the }\frac{1}{3}\end{aligned}$

This is an exact solution. If we are asked for a decimal approximation, we can use a calculator to get:

$x\approx -0.0279$

We can also use this approximate value for $x$ to check our solution in the original equation. The left side of the equation should equal approximately 10:

$4e^{3x}e=4e^{3(-0.0279)}e=10.0000$

Try It 4

Solve the equation $7e^{5x+4}=e$ . Round the answer to 5 decimal places and use this approximation to check your exact solution.

Show Answer

x = - 0.98918

$x=-0.98918$

Example 5

Solve the equation $2^{4x-3}=5^x$ .

Solution

$\begin{aligned}2^{4x-3}&=5^x\\\\\log{2^{4x-3}}&=\log{5^x}&&\text{Take the common log of both sides of the equation}\\\\(4x-3)\log{2}&=x\log{5}&&\text{Pull the exponents in front of the logarithms}\\\\4x \log{2} -3\log2&=x\log5&&\text{Distribute the constant }\log2\\\\ 4x\log{2}-x\log5&=3\log2&&\text{Get all variables terms on the same side and constants on the other side}\\\\x\left(4\log{2}-\log(5)\right)&=3\log{2}&&\text{Factor out }x\text{ on the left side}\\\\x&=\dfrac{3\log{2}}{4\log{2}-\log{5}}&&\text{Divide both sides by the constant }\left(\log2-\log5\right)\end{aligned}$

To check our solution we can find an approximation to our answer:

$x=\dfrac{3\log{2}}{4\log{2}-\log{5}}\approx 1.787766$

Check:

$2^{4x-3}=2^{4(1.787766)-3}=17.76621$

$5^x=5^{1.787766}=17.6621$

Try It 5

Solve the equation $3^{6x+1}=7^x$ . Round the answer to 6 decimal places and use this approximation to check your exact solution.

Show Answer

The exact solution may look different depending on which base of logarithm you use. Here are four possibilities:

$x=\dfrac{\ln3}{\ln7-6\ln3}$ using natural logs

$x=\dfrac{\log3}{\log7-6\log3}$ using common logs

$x=\dfrac{1}{\log_3{7}-6}$ using base 3 logs

$x=\dfrac{\log_7{3}}{1-6\log_7{3}}$ using base 7 logs

All solutions give the approximate decimal answer $x=-0.236476$

Don’t forget that solving the equation $3^{6x+1}=7^x$ means we are finding the point of intersection of the functions $f(x)=3^{6x+1}$ and $g(x)=7^x$ (figure 4), so determining the point of intersection graphically is also a way to check our solution.

intersection of two exponential functions

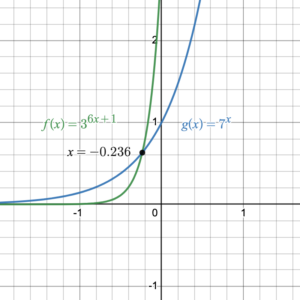
Figure 4. The intersection of two functions

Example 6

Solve the equation $5^{3x+2}=2^{2x-5}$ .

Solution

$\begin{aligned}5^{3x+2}&=2^{2x-5}\\\\ \log_5{5^{3x+2}}&=\log_5{2^{2x-5}}\\\\(3x+2)\log_5{5}&=(2x-5)\log_5{2}\\\\ 3x+2&=2x\log_5{2}-5\log_5{2}\\\\ 2+5\log_5{2}&=2x\log_5{2}-3x\\\\2+5\log_5{2}&=x\left(2\log_5{2}-3\right)\\\\\dfrac{2+5\log_5{2}}{2\log_5{2}-3}&=x\end{aligned}$

Check

Using a calculator, this exact solution is approximately -1.942061

$5^{3x+2}\approx 5^{3(-1.942061)+2}\approx 0.0021$

$2^{2x-5}\approx 2^{2(-1.942061)-5}\approx 0.0021$

Try It 6

Solve the equation $8^{2x-3}=4^{x+5}$ .

Show Answer

$x=\dfrac{19}{4}$

Notice that Try It 6 could have been solved using the equality of bases:

$\begin{aligned}8^{2x-3}&=4^{x+5}\\\\\left(2^3\right)^{2x-3}&=\left(2^2\right)^{x+5}\\\\2^{6x-9}&=2^{2x+10}\\\\6x-9&=2x+10\\\\4x&=19\\\\x&=\dfrac{19}{4}\end{aligned}$

Deciding which method to use when solving exponential equations:

If $a^M=C$ , where $C$ is a constant and $M$ is a function of $x$ , rewrite an equivalent equation in terms of logarithms or take logarithms on both sides of the equation, and then solve for $x$ .

If $a^M=b^N$ where $M$ and $N$ are functions of $x$ , and $a$ and $b$ are both powers of the same number (e.g., 4 and 8 are both some powers of 2, write the equation using the common base then equate the exponents.

Otherwise, take the logarithm of both sides of the equation. Use natural or common logarithms or logarithms of base $a$ or $b$ for the most concise algebra.

Chapter 6: Logarithmic Functions