Learning Objectives
- Explain the definition of a rational function
- Use Desmos to graph rational functions
- Determine the Domain and Range of rational functions
- Determine the vertical and horizontal asymptotes of rational functions
Definition of Rational Functions
A rational function has the form [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex], where [latex]P(x)[/latex] and [latex]Q(x)[/latex] are polynomials. In addition, [latex]Q(x)\neq 0[/latex]. The expression [latex]\dfrac{P(x)}{Q(x)}[/latex] is called a rational expression. Examples of rational functions include: [latex]f(x)=\dfrac{1}{x}[/latex], [latex]f(x)=\dfrac{5x-3}{x^2-1}[/latex], [latex]h(x)=\dfrac{x^2-5}{x^3+2x^2+7}[/latex], [latex]g(x)=\dfrac{7x^3-5x}{x^2-5}[/latex].
Graphs of Rational Functions
We can use Desmos to graph rational functions. Try it out for yourself. Figure 1 shows some examples.
| Examples of Rational Functions |
 |
 |
 |
 |
| Figure 1. Examples of the graphs of rational functions |
Domain and Range
Each function has a domain and a range. The domain is the set of all [latex]x[/latex]-values, while the range is the set of all [latex]y[/latex]-values.
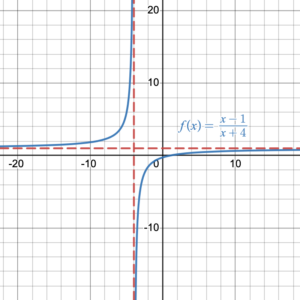
The domain for the function [latex]f(x)=\dfrac{x-1}{x+4}[/latex] is all real numbers except [latex]x=-4[/latex]. It can be written in interval notation as [latex]x\in(-\infty,\,-4)\cup(-4,\,+\infty)[/latex] or in set notation as [latex]\{x\;|\;x \in \mathbb{R}, x\neq -4\}[/latex]. The point [latex]x=-4[/latex] is excluded from the domain because at that point the function value is undefined: [latex]f(-4)=\dfrac{-4-1}{-4+4}=\dfrac{-5}{0}[/latex], and we can’t divide by zero. [latex]x=-4[/latex] is called a restriction on the domain. The line [latex]x=-4[/latex] is a vertical asymptote (Figure 1: top left).
The range of the function [latex]f(x)=\dfrac{x-1}{x+4}[/latex] is all real numbers except [latex]y=1[/latex]. It can be written in interval notation as [latex]y\in(-\infty,\,1)\cup(1,\,+\infty)[/latex] or in set notation as [latex]\{y\;|\;y \in \mathbb{R}, y\neq 1\}[/latex]. There is a horizontal asymptote at [latex]y=1[/latex] (Figure 1: top left). Horizontal asymptotes appear on the graphs of rational functions [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] when the degree of [latex]P(x)[/latex] is less than or equal to the degree of [latex]Q(x)[/latex]. In this case the degrees are equal at 1. When the degrees are equal, the horizontal asymptote is found by dividing the leading coefficients of [latex]P(x)[/latex] and [latex]Q(x)[/latex]. In this case, the horizontal asymptote is [latex]y=\dfrac{1}{1}=1[/latex].
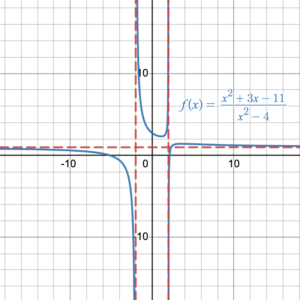
The domain for the function [latex]f(x)=\dfrac{1}{x^2-1}[/latex] is all real numbers except [latex]x=-1[/latex] and [latex]x=1[/latex]. It can be written in interval notation as [latex]x\in(-\infty,\,-1)\cup(-1,\,1)\cup(1,\,+\infty)[/latex] or in set notation as [latex]\{x\;|\;x \in \mathbb{R}, x\neq \pm1\}[/latex]. The points [latex]x=-1[/latex] and [latex]x=1[/latex] are excluded from the domain because at those points the function value is undefined. [latex]x=-1[/latex] and [latex]x=1[/latex] are restrictions on the domain. The lines [latex]x=-1[/latex] and [latex]x=1[/latex] are vertical asymptotes (Figure 1: top right).
The range for the function [latex]f(x)=\dfrac{1}{x^2-1}[/latex] can be seen from the graph to exclude the [latex]y[/latex]-values greater than –1 and less than or equal to 0. That means the domain is all real numbers except [latex]-1
RESTRICTIONS ON THE DOMAIN
The rational function [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] has restrictions on the domain when [latex]Q(x)=0[/latex].
Example 1
State the domain and range of the function [latex]f(x)=\dfrac{x^2+3x-11}{x^2-4}[/latex].
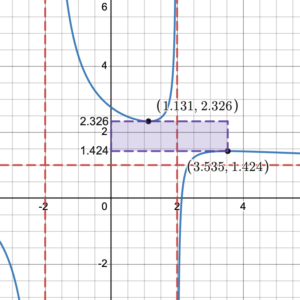
Zoomed in view of [latex]f(x)=\dfrac{x^{2}+3x-11}{x^2-4}[/latex]
Solution
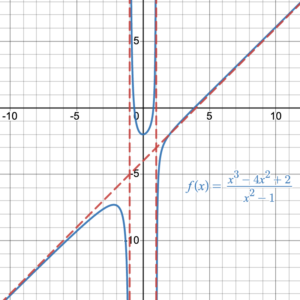
This function is graphed in figure 1 (bottom left). It has vertical asymptotes at [latex]x=\pm2[/latex], therefore [latex]x=\pm2[/latex] are restrictions on the domain.
In interval notation Domain = [latex](-\infty,\,-2)\cup(-2,\,2)\cup(2,\,+\infty)[/latex]
In set notation Domain = [latex]\{x\;|\;x \in \mathbb{R}, x\neq \pm2\}[/latex]
The graph has a horizontal asymptote at [latex]y=1[/latex] but this asymptote is crossed by the function just at [latex]x=2.333[/latex] so must be included in the range. There is however a gap in the range values from the highest point on the lower right part of the graph and the turning point on the upper part of the curve. We can use Desmos to determine the approximate value of these points by moving the curser over the graph. So, the range is [latex]y\in(-\infty,\,1.424]\cup[2.326,\,+\infty)[/latex] in interval notation, and [latex]\{y\;|\;y \in \mathbb{R}, y \not \in [1.424, 2.326]\}[/latex] in set notation.
Try It 1
- Use Desmos to graph the function [latex]f(x)=\dfrac{3x+4}{x-2}[/latex].
- What is the vertical asymptote?
- What is the horizontal asymptote?
- Determine the domain of the function. Write it in set notation.
- Determine the range of the function. Write it in interval notation.
Show Answer
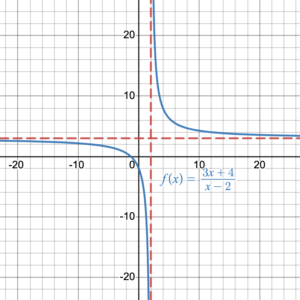
- [latex]x=2[/latex]
- [latex]y=3[/latex]
- Domain = [latex]\{x\;|\;x \in \mathbb{R}, x\neq \pm2\}[/latex]
- Range = [latex]y\in(-\infty,\,3)\cup(3,\,+\infty)[/latex]
Vertical Asymptotes
Have you noticed the relationship between the vertical asymptotes and the restrictions on the domain?
For example,
| Function |
Restriction on the domain |
Vertical asymptote |
| [latex]f(x)=\dfrac{x-1}{x+4}[/latex] |
[latex]x=-4[/latex] |
[latex]x=-4[/latex] |
| [latex]f(x)=\dfrac{1}{x^2-1}[/latex] |
[latex]x=\pm1[/latex] |
[latex]x=\pm1[/latex] |
| [latex]f(x)=\dfrac{x^2+3x-11}{x^2-4}[/latex] |
[latex]x=\pm2[/latex] |
[latex]x=\pm2[/latex] |
A vertical asymptote is a vertical line that passes through the restricted value of the domain. The vertical asymptote can never be crossed by the graph, since the graph is undefined at that value.
We can easily find any vertical asymptotes by determining the restrictions on the domain. For a rational function [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] the domain will be restricted when the denominator, [latex]Q(x)[/latex], is equal to zero. This is because division by zero is undefined.
VERTICAL ASYMPTOTES
The rational function [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] will have vertical asymptotes at [latex]Q(x)=0[/latex].
Example 2
Determine the vertical asymptote(s) of the function [latex]f(x)=\dfrac{3x}{x^2-3x-4}[/latex].
Solution
Vertical asymptotes occur at restrictions on the domain. The domain is restricted at [latex]x[/latex]-values that cause the denominator of the function to equal zero.
So we set the denominator to zero and solve for [latex]x[/latex]:
[latex]x^2-3x-4=0[/latex]
To solve for [latex]x[/latex], we can factor the quadratic then use the zero product property:
[latex]\begin{aligned}x^2-3x-4&=0\\\\(x-4)(x+1)&=0\\\\x=4,\,x&=-1\end{aligned}[/latex]
The vertical asymptotes are [latex]x=4[/latex] and [latex]x=-1[/latex].
Try It 2
Determine the vertical asymptote of the function [latex]f(x)=\dfrac{2x-5}{x^2-9}[/latex].
Show Answer
[latex]x=\pm3[/latex]
Horizontal Asymptotes
Horizontal asymptotes appear on the graph of a rational function [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] when the degree of [latex]P(x)[/latex] is less than or equal to the degree of [latex]Q(x)[/latex].
HORIZONTAL ASYMPTOTES
The rational function [latex]f(x)=\dfrac{P(x)}{Q(x)}[/latex] will have a horizontal asymptote when the degree of [latex]P(x)[/latex] is less than or equal to the degree of [latex]Q(x)[/latex].
If the degree [latex]P(x)[/latex] is less than the degree of [latex]Q(x)[/latex], the horizontal asymptote will be [latex]y=0[/latex].
If the degree [latex]P(x)[/latex] is equal to the degree of [latex]Q(x)[/latex], the horizontal asymptote will be [latex]y=\dfrac{\text{Leading coefficient of }P(x)}{\text{Leading coefficient of }Q(x)}[/latex].
Example 3
Determine the horizontal asymptotes of the graphs of the function:
- [latex]f(x)=\dfrac{4x-5}{2x+7}[/latex]
- [latex]f(x)=\dfrac{9x^2-1}{3x^2+2}[/latex]
- [latex]f(x)=\dfrac{x-3}{2x^2+6x-3}[/latex]
- [latex]f(x)=\dfrac{x^3-5}{x+7}[/latex]
Solution
- [latex]P(x)=4x-5[/latex] has degree 1. [latex]Q(x)=2x+7[/latex] has degree 1. Since the degrees are equal, the horizontal asymptote is found by dividing the leading coefficients: [latex]y=\dfrac{4}{2}=2[/latex].
- [latex]P(x)=9x-1[/latex] has degree 2. [latex]Q(x)=3x^2+2[/latex] has degree 2. Since the degrees are equal, the horizontal asymptote is found by dividing the leading coefficients: [latex]y=\dfrac{9}{3}=3[/latex].
- [latex]P(x)=x-3[/latex] has degree 1. [latex]Q(x)=2x^2+6x-3[/latex] has degree 2. Since the degree of [latex]P(x)[/latex] is less than the degree of [latex]Q(x)[/latex], the horizontal asymptote is [latex]y=0[/latex].
- [latex]P(x)=x^3-5[/latex] has degree 3. [latex]Q(x)=x+7[/latex] has degree 1. Since the degree of [latex]P(x)[/latex] is greater than the degree of [latex]Q(x)[/latex], there is no horizontal asymptote.
Try It 3
Determine the horizontal asymptotes of the graphs of the function:
- [latex]f(x)=\dfrac{14x-3}{7x+4}[/latex]
- [latex]f(x)=\dfrac{2x^2-1}{3x^3+2}[/latex]
- [latex]f(x)=\dfrac{x^3-3}{2x^2}[/latex]
- [latex]f(x)=\dfrac{x^2-5}{4x^2+7}[/latex]
Show Answer
- [latex]y=2[/latex]
- [latex]y=0[/latex]
- There is no horizontal asymptote
- [latex]y=\dfrac{1}{4}[/latex]
Candela Citations
CC licensed content, Original
- Rational Functions and Their Graphs. Authored by: Hazel McKenna . Provided by: Utah Valley University. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna. Provided by: Utah Valley University. Located at: http://www.desmos.com/calculator. License: CC BY: Attribution
- All examples and Try Its: hjm858; hjm607; hjm098; . Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution






