Learning Outcomes
- Evaluate exponential expressions
- Evaluate square root expressions
Key words
- Exponential expression: notation to write repeated multiplication
- Base: the number being raised to a power in an exponential expression
- Exponent: the power the base is being raised to in an exponential expression
- Radical: the sign used to indicate square root: [latex]\sqrt{}[/latex]
- Square root: a number when squared gives the number under the radical
Exponential Expressions
Just as multiplication is repeated addition, we use exponential notation to write repeated multiplication of the same quantity. For example, [latex]{2}^{4}[/latex] means to multiply [latex]2[/latex] by itself four times, So, [latex]{2}^{4}[/latex] means [latex]2\cdot 2\cdot 2\cdot 2[/latex]. Conversely, [latex]10\cdot10\cdot10[/latex] can be written more succinctly as [latex]10^{3}[/latex]. The [latex]10[/latex] in [latex]10^{3}[/latex] is called the base. The [latex]3[/latex] in [latex]10^{3}[/latex] is called the exponent. The expression [latex]10^{3}[/latex] is called the exponential expression. Knowing the names for the parts of an exponential expression will help you learn how to perform mathematical operations on them.
Exponential Notation
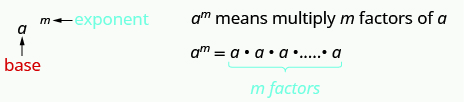
This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we multiply the base [latex]a[/latex] by itself.

[latex]10^{3}[/latex] is read as “[latex]10[/latex] to the third power” or “[latex]10[/latex] cubed.” It means [latex]10\cdot10\cdot10[/latex], or [latex]1,000[/latex].
[latex]8^{2}[/latex] is read as “[latex]8[/latex] to the second power” or “[latex]8[/latex] squared.” It means [latex]8\cdot8[/latex], or [latex]64[/latex].
[latex]5^{4}[/latex] is read as “[latex]5[/latex] to the fourth power.” It means [latex]5\cdot5\cdot5\cdot5[/latex], or [latex]625[/latex].
If the exponential expression is negative, such as [latex]−3^{4}[/latex], it means [latex]–\left(3\cdot3\cdot3\cdot3\right)[/latex] or [latex]−81[/latex].
If [latex]−3[/latex] is to be the base, it must be written as [latex]\left(−3\right)^{4}[/latex], which means [latex](−3)\cdot(−3)\cdot(−3)\cdot(−3)=81[/latex].
You can see that there is quite a difference, so you have to be very careful! The following examples show how to identify the base and the exponent, as well as how to identify the expanded and exponential format of writing repeated multiplication.
Example
Identify the exponent and the base in the following terms, then simplify:
- [latex]7^{2}[/latex]
- [latex]2^{3}[/latex]
- [latex]-5^{2}[/latex]
- [latex]\left(-5\right)^{2}[/latex]
example
Simplify:
1. [latex]{5}^{3}[/latex]
2. [latex]{9}^{1}[/latex]
Solution
| 1. | |
| [latex]{5}^{3}[/latex] | |
| Multiply [latex]3[/latex] factors of [latex]5[/latex]. | [latex]5\cdot 5\cdot 5[/latex] |
| Simplify. | [latex]125[/latex] |
| 2. | |
| [latex]{9}^{1}[/latex] | |
| Multiply [latex]1[/latex] factor of [latex]9[/latex]. | [latex]9[/latex] |
try it
example
Simplify:
1. [latex]{\left(-3\right)}^{4}[/latex]
2. [latex]{-3}^{4}[/latex]
try it
Simplify Expressions with Square Roots
Remember that when a number [latex]n[/latex] is multiplied by itself, we can write this as [latex]{n}^{2}[/latex], which we read aloud as “n squared”. For example, [latex]{8}^{2}[/latex] is read as “8 squared”.
We call [latex]64[/latex] the square of [latex]8[/latex] because [latex]{8}^{2}=64[/latex]. Similarly, [latex]121[/latex] is the square of [latex]11[/latex], because [latex]{11}^{2}=121[/latex].
Square of a Number
If [latex]{n}^{2}=m[/latex], then [latex]m[/latex] is the square of [latex]n[/latex].
Modeling Squares
Do you know why we use the word square? If we construct a square with three tiles on each side, the total number of tiles would be nine.
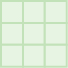
This is why we say that the square of three is nine.
[latex]{3}^{2}=9[/latex]
The number [latex]9[/latex] is called a perfect square because it is the square of a whole number.
The chart shows the squares of the natural numbers [latex]1[/latex] through [latex]15[/latex]. You can refer to it to help you identify the perfect squares.

Perfect Squares
A perfect square is the square of a rational number.
What happens when you square a negative number?
[latex]\begin{array}{cc}\hfill {\left(-8\right)}^{2}& =\left(-8\right)\left(-8\right)\\ & =64\hfill \end{array}[/latex]
When we multiply two negative numbers, the product is always positive. So, the square of a negative number is always positive.
The chart shows the squares of the negative integers from [latex]-1[/latex] to [latex]-15[/latex].

Did you notice that these squares are the same as the squares of the positive numbers?
Square Roots
Sometimes we will need to look at the relationship between numbers and their squares in reverse. Because [latex]{10}^{2}=100[/latex], we say [latex]100[/latex] is the square of [latex]10[/latex]. We can also say that [latex]10[/latex] is a square root of [latex]100[/latex].
Square Root of a Number
If [latex]{n}^{2}=m[/latex], then [latex]n[/latex] is a square root of [latex]m[/latex].
Notice [latex]{\left(-10\right)}^{2}=100[/latex] also, so [latex]-10[/latex] is also a square root of [latex]100[/latex]. Therefore, both [latex]10[/latex] and [latex]-10[/latex] are square roots of [latex]100[/latex].
So, every positive number has two square roots: one positive and one negative.
What if we only want the positive square root of a positive number? The radical sign, [latex]\sqrt{\phantom{0}}[/latex], stands for the positive square root. The positive square root is also called the principal square root.
Square Root Notation
[latex]\sqrt{m}[/latex] is read as “the square root of [latex]m\text{."}[/latex]
If [latex]m={n}^{2}[/latex] then [latex]\sqrt{m}=n[/latex] for [latex]{n}\ge 0[/latex].
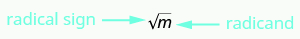
We can also use the radical sign for the square root of zero. Because [latex]{0}^{2}=0,\sqrt{0}=0[/latex]. Notice that zero has only one square root.
The chart shows the square roots of the first [latex]15[/latex] perfect square numbers.

example
Simplify: (a) [latex]\sqrt{25}[/latex] (b) [latex]\sqrt{121}[/latex]
Solution
(a) [latex]\sqrt{25}=5[/latex] since [latex]{5}^{2}=25[/latex]
(b) [latex]\sqrt{121}=11[/latex] since [latex]{11}^{2}=121[/latex]
try it
The following video shows several more examples of how to simplify the square root of a perfect square.
Every positive number has two square roots and the radical sign indicates the positive one. We write [latex]\sqrt{100}=10[/latex]. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, [latex]-\sqrt{100}=-10[/latex].
example
Simplify. (a) [latex]-\sqrt{9}[/latex] (b) [latex]-\sqrt{144}[/latex]
try it
Square Root of a Negative Number
Can we simplify [latex]\sqrt{-25}?[/latex] Is there a number whose square is [latex]-25?[/latex]
[latex]{\left(?\right)}^{2}=-25[/latex]
None of the numbers that we have dealt with so far have a square that is [latex]-25[/latex]. Why? Any positive number squared is positive, and any negative number squared is also positive. We say there is no real number equal to [latex]\sqrt{-25}[/latex]. If we are asked to find the square root of any negative number, we say that the solution is not a real number.
example
Simplify: (a) [latex]\sqrt{-169}[/latex] (b) [latex]-\sqrt{121}[/latex].
try it
Candela Citations
- Simplifying Square Roots (Perfect Squares). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/rDpIm_EepcE. License: CC BY: Attribution
- Adaption and Revision. Authored by: Roxanne Brinkerhoff. Provided by: Utah Valley University. License: CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. License: CC BY: Attribution
