Learning Objectives
- Write a linear equation in slope-intercept form.
- Identify the slope and [latex]y[/latex]-intercept given a linear equation.
- Write the linear equation of a graphed line.
- Graph a linear equation in slope-intercept form.
Key words
- Slope-intercept form: a linear equation in the form [latex]y=mx+b[/latex]
Slope-Intercept Form
When an equation is written in the form [latex]y = mx+b[/latex] it is said to be in slope-intercept form. Let’s see why it has that name. Consider the equation [latex]y=2x+3[/latex]. If we set [latex]x=0[/latex], then [latex]y=2(0)+3=3[/latex]. This means that the point [latex](0, 3)[/latex] is the [latex]y[/latex]-intercept of the line formed by the equation.
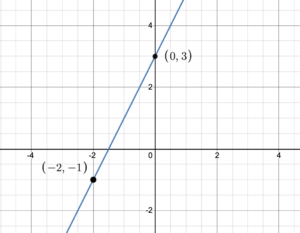
Figure 1. Graph of [latex]y=2x+3[/latex]
The graph in figure 1, also shows that the point [latex](-2 -1)[/latex] lies on the graph. Consequently, the slope of the line is [latex]m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-(-1)}{0-(-2)}=\frac{4}{2}=2[/latex]. This is the coefficient of [latex]x[/latex] in the equation [latex]y=2x+3[/latex]. So with slope = [latex]m[/latex] and the [latex]y[/latex]-intercept [latex]= (0, b)[/latex], the equation written in the form [latex]y=mx+b[/latex] immediately tells us the slope, [latex]m[/latex], and the [latex]y[/latex]-intercept, [latex](0, b)[/latex].
Slope-Intercept Form of a Linear Equation
In the equation [latex]y=mx+b[/latex],
- [latex]m[/latex] is the slope of the graph.
- [latex]b[/latex] is the [latex]y[/latex]-coordinate of the [latex]y[/latex]-intercept [latex](0, b)[/latex] of the graph.
Examples
Find the slope and [latex]y[/latex]-intercept of the line with the given equation:
1. [latex]y=-3x+7[/latex]
2. [latex]y=\frac{2}{3}x-\frac{1}{5}[/latex]
3. [latex]2x-3y=6[/latex]
Solution
1. [latex]m=-3\text{ and }b=7\text{ so the slope is }-3\text{ and the }y\text{-intercept is the point } (0, 7)[/latex]
2. [latex]m=\frac{2}{3}\text{ and }b=-\frac{1}{5}\text{ so the slope is }\frac{2}{3}\text{ and the }y\text{-intercept is the point } \left (0,-\frac{1}{5}\right )[/latex]
3. We first have to rearrange the equation to solve for [latex]y[/latex]:
[latex]\begin{equation}\begin{aligned}2x-3y & = 6 \\ -3y & = -2x+6 \\ y & = \frac{2}{3}x-2\end{aligned}\end{equation}[/latex]
[latex]\text{So, }m=\frac{2}{3}\text{ and }b=-2\text{ so the slope is }\frac{2}{3}\text{ and the }y\text{-intercept is the point } \left (0,2\right )[/latex]
Try It
Find the slope and [latex]y[/latex]-intercept of the line with the given equation:
1. [latex]y=6x-1[/latex]
2. [latex]y=\frac{4}{7}x-\frac{2}{3}[/latex]
3. [latex]5x-y=10[/latex]
We can also find the linear equation that represents te graph of a line If we know the slope and the [latex]y[/latex]-intercept.
Example
Write the equation of the line that has a slope of [latex]\displaystyle \frac{1}{2}[/latex] and a y-intercept of [latex](0, −5)[/latex].
Solution
Substitute the slope, [latex]m[/latex], into [latex]y=mx+b[/latex].
[latex]\displaystyle y=\frac{1}{2}x+b[/latex]
Substitute [latex]b[/latex], into the equation.
[latex]\displaystyle y=\frac{1}{2}x-5[/latex]
Answer
[latex]y=\frac{1}{2}x-5[/latex]
Example
Write the equation of the line in the graph by identifying the slope and [latex]y[/latex]-intercept.
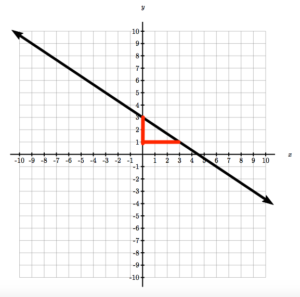Solution
Identify the point where the graph crosses the [latex]y[/latex]-axis [latex](0,3)[/latex]. This means that [latex]b=3[/latex]. Identify one other point and draw a slope triangle to find the slope.
Slope: [latex]m=\frac{-2}{3}[/latex].
Substitute [latex]m[/latex] and [latex]b[/latex] into the slope-intercept equation.
[latex]y=mx+b\\y=\frac{-2}{3}x+b\\y=\frac{-2}{3}x+3[/latex]
Answer
[latex]y=\frac{-2}{3}x+3[/latex]
When we are given an equation in the slope-intercept form of [latex]y=mx+b[/latex], we can identify the slope and y-intercept and use these to graph the equation. When we have an equation in slope-intercept form we can graph it by first plotting the [latex]y[/latex]-intercept, then using the slope to find a second point, and connecting the dots.
Example
Graph [latex]y=\frac{1}{2}x-4[/latex] using the slope-intercept equation.
Solution
First, plot the [latex]y[/latex]-intercept.
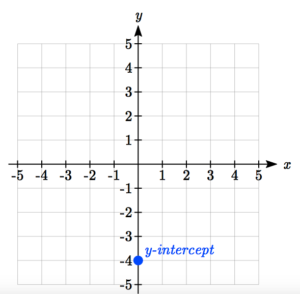
Now use the slope to count up or down and over left or right to the next point. This slope is [latex]\frac{1}{2}[/latex], so we can count up one and right two—both positive because both parts of the slope are positive.
Connect the dots.
NOTE: it is important for the equation to first be in slope-intercept form. If it is not, we have to solve it for [latex]y[/latex] so we can identify the slope and the [latex]y[/latex]-intercept.
Try It
Watch the video below for another example of how to write the equation of the line, when given a graph, by identifying the slope and y-intercept.
