Learning Outcomes
- Use the substitution method to solve systems of linear equations
- Express the solution of an inconsistent system of equations containing two variables
- Express the solution of a dependent system of equations containing two variables
Key words
- Contradiction: a statement that is always false
- Identity: a statement that is always true
The Substitution Method
In this section we will learn the substitution method for finding a solution to a system of linear equations in two variables. We have used substitution to verify the solution of an equation, when we substituted values in for the [latex]x[/latex] and [latex]y[/latex] variables. The idea is similar when applied to solving systems.
First we make the assumption that a system of equations has a solution. This means that the lines cross at a single point, which is turn means that at that point, the [latex]x[/latex]-values and the [latex]y[/latex]-values in each equation are the same. This allows us to substitute either an [latex]x[/latex]-value or a [latex]y[/latex]-value from one equation into the other equation. The goal of the substitution method is to rewrite one of the equations in terms of a single variable. Then that equation can be solved for one of the variables. The second variable is found by substituting its new found value into either of the original equations and solving for the second variable.
Let’s start with an example to see what this means.
Example
Find the solution of the system:
[latex]4x+3y=−14//y=2[/latex]
Solution
The second equation already gives us the value of [latex]y[/latex]: [latex]y=2[/latex]
We are going to substitute this value of [latex]y=2[/latex] into the first equation:
[latex]4x+3y=−14[/latex]
[latex]4x+3\left(\color{red}{2}\right)=−14[/latex]
No simplify and solve the equation for [latex]x[/latex].
[latex]\begin{array}{r}4x+6=−14\\4x=−20\\x=−5\,\,\,\end{array}[/latex]
Answer
[latex](-5,2)[/latex] is the solution of the system of equations.
We can substitute a variable even if it is written as an expression.
Example
Solve the system of equations:
[latex]y+x=3\\x=y+5[/latex]
Solution
The goal of the substitution method is to rewrite one of the equations in terms of a single variable. The second equation tells us that [latex]x=y+5[/latex], so we can substitute [latex]y+5[/latex] for [latex]x[/latex] in the first equation:
[latex]\begin{array}{r}y+\color{red}{x}=3\\y+\color{red}{\left(y+5\right)}=3\end{array}[/latex]
Simplify and solve the equation for [latex]y[/latex]:
[latex]\begin{array}{r}2y+5=\,\,\,\,3\\\underline{−5\,\,\,\,\,−5}\\2y=−2\\y=−1\end{array}[/latex]
Now find [latex]x[/latex] by substituting this value for [latex]y[/latex] into either equation and solving for [latex]x[/latex].
We will use the first equation:
[latex]\begin{array}{r}\color{red}{y}+x=3\\\color{red}{−1}+x=3\\\underline{+1\,\,\,\,\,\,\,\,\,+1}\\x=4\end{array}[/latex]
Finally, check the solution [latex]x=4[/latex], [latex]y=−1[/latex] by substituting these values into each of the original equations.
[latex]\begin{array}{r}y+x=3\\−1+4=3\\3=3\\\text{TRUE}\end{array}[/latex]
[latex]\begin{array}{l}x=y+5\\4=−1+5\\4=4\\\text{TRUE}\end{array}[/latex]
Answer
[latex]x=4[/latex] and [latex]y=−1[/latex]
The solution is [latex](4,−1)[/latex].
Remember, a solution to a system of equations must be a solution to each of the equations within the system. The ordered pair [latex](4,−1)[/latex] does work for both equations, so we know that it is a solution to the system as well.
Try It
Solve the system of equations: [latex]2x+3y=6\\x=-3[/latex]
Try It
Solve the system of equations: [latex]2x+3y=6\\y=3x+2[/latex]
In the examples above, one of the equations was already given to us in terms of the variable [latex]x[/latex] or [latex]y[/latex]. This allowed us to quickly substitute that value into the other equation and solve for one of the unknowns.
Sometimes we have to rewrite one of the equations in terms of one of the variables first before we can substitute.
Example
Solve the following system of equations by substitution.
Solution
Solve the first equation for [latex]y[/latex]:
Substitute the expression [latex]x - 5[/latex] for [latex]y[/latex] in the second equation:
Substitute [latex]x=8[/latex] into the first equation and solve for [latex]y[/latex]:
Our solution is [latex]\left(8,3\right)[/latex].
Check the solution by substituting [latex]\left(8,3\right)[/latex] into both equations.
[latex]\begin{equation}\begin{aligned}-x+y & =-5 \\ -(8)+(3) & =-5 \;\;\;\;\;\text{True}\\ \\2x - 5y & =1 \\ 2\left(8\right)-5\left(3\right) &=1 \;\;\;\;\;\text{True}\end{aligned}\end{equation}[/latex]
Answer
[latex]\left(8,3\right)[/latex]
The substitution method can be used to solve any linear system in two variables, but the method works best if one of the equations contains a coefficient of 1 or [latex]–1[/latex] so that we do not have to deal with fractions.
Here is a summary of the steps we use to solve systems of equations using the substitution method.
solvING A SYSTEM OF LINEAR EQUATIONS using the substitution method
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the unused equation, and then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the other variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Let’s look at some examples whose substitution involves the distributive property.
Example
Solve the system of equations.
[latex]\begin{array}{l}y = 3x + 6\\−2x + 4y = 4\end{array}[/latex]
Solution
The first equation is already solved for [latex]y[/latex] in terms of [latex]x[/latex], so it makes sense to substitute [latex]3x + 6[/latex] into the second equation for [latex]y[/latex]:
[latex]\begin{array}{r}−2x+4y=4\\−2x+4\left(3x+6\right)=4\end{array}[/latex]
Simplify and solve the equation for [latex]x[/latex]:
[latex]\begin{array}{r}−2x+12x+24=4\,\,\,\,\,\,\,\\10x+24=4\,\,\,\,\,\,\,\\\underline{−24\,\,−24\,\,\,\,}\\10x=−20\\x=−2\,\,\,\end{array}[/latex]
To find[latex]y[/latex], substitute this value for [latex]x[/latex] back into one of the original equations.
[latex]\begin{array}{l}y=3x+6\\y=3\left(−2\right)+6\\y =−6+6\\y=0\end{array}[/latex]
Check the solution [latex]x=−2[/latex], [latex]y=0[/latex] by substituting them into each of the original equations.
[latex]\begin{array}{l}y=3x+6\\0=3\left(−2\right)+6\\0=−6+6\\0=0\\\text{TRUE}\end{array}[/latex]
[latex]\begin{array}{r}−2x+4y=4\\−2\left(−2\right)+4\left(0\right)=4\\4+0=4\\4=4\\\text{TRUE}\end{array}[/latex]
Answer
[latex]x=−2[/latex] and [latex]y=0[/latex]
The solution is [latex](−2, 0)[/latex].
Example
Solve the system of equations.
[latex]\begin{array}{r}2x+3y=22\\3x+y=19\end{array}[/latex]
Solution
The second equation,[latex]3x+y=19[/latex], can easily be rewritten in terms of [latex]y[/latex]:
[latex]\begin{array}3x+y=19\\y=19–3x\end{array}[/latex]
Substitute [latex]19–3x[/latex] for [latex]y[/latex] in the other equation:
[latex]\begin{array}{r}2x+3y=22\\2x+3(19–3x)=22\end{array}[/latex]
Simplify and solve the equation for [latex]x[/latex]:
[latex]\begin{array}{r}2x+57–9x=22\,\,\,\,\\−7x+57=22\,\,\,\,\\−7x=−35\\x=5\,\,\,\,\,\,\,\end{array}[/latex]
Substitute [latex]x=5[/latex] back into one of the original equations to solve for [latex]y[/latex].
[latex]\begin{array}{r}3x+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\3\left(5\right)+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\15+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\y=19−15\\y=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Check both solutions by substituting them into each of the original equations.
[latex]\begin{array}{r}2x+3y=22\\2(5)+3\left(4\right)=22\\10+12=22\\22=22\\\text{TRUE}\\\\3x+y=19\\3\left(5\right)+4= 19\\19=19\\\text{TRUE}\end{array}[/latex]
Answer
[latex]x=5[/latex] and [latex]y=4[/latex]
The solution is [latex](5, 4)[/latex].
If we had chosen the other equation to start with in the previous examples, we would still be able to find the same solution. It is really a matter of preference because sometimes solving for a variable will result in having to work with fractions. Gaining experience with algebra, will help us to anticipate what choices will lead to more desirable outcomes.
Try It
Solve the system of equations.
[latex]\begin{array}{r}x+3y=6\\3y=x-6\end{array}[/latex]
The following video shows an example of solving a systems of two equations using the substitution method.
Try It
Inconsistent and Dependent Systems
Not all systems have a single solution. Inconsistent systems have no solution, and dependent systems have infinite solutions represented by an equation. When we started solving systems using substitution, we made the assumption that there is exactly one solution. That assumption will be shown to be false if we get either a contradiction (e.g., [latex]2=-6[/latex]) or an identity (e.g., [latex]4=4[/latex].
A contradiction implies there are no solutions to this equation. An identity implies that the system is dependent and has infinite solutions that are represented by either equation.
Example
Solve the system of equations.
[latex]\begin{array}{l}y=5x+4\\10x−2y=4\end{array}[/latex]
Solution
Since the first equation is [latex]y=5x+4[/latex], we can substitute [latex]5x+4[/latex] in for [latex]y[/latex] in the second equation:
[latex]\begin{array}{r}y=5x+4\\10x−2y=4\,\,\,\,\,\,\,\,\,\,\,\,\\10x–2\left(5x+4\right)=4\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Expand the expression on the left using the distributive property:
[latex]10x–10x–8=4[/latex]
Combine like terms on the left side of equation:
[latex]10x–10x=0[/latex], so you are left with [latex]−8=4[/latex]; a contradiction.
Answer
The statement [latex]−8=4[/latex] is false, so there is no solution.
We get the contradiction [latex]−8=4[/latex]. What does this mean? The graph of this system sheds some light on what is happening.
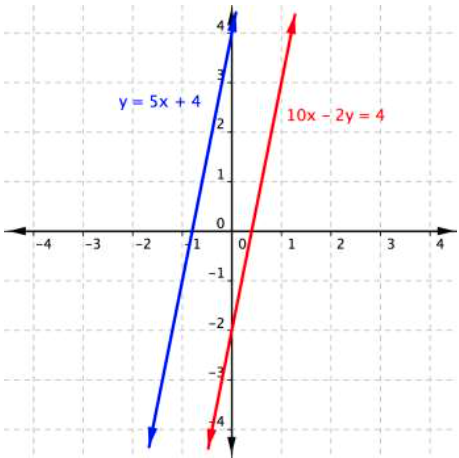
The lines are parallel, they never intersect and there is no solution to this system of linear equations. Note that the result [latex]−8=4[/latex] is not a solution. It is simply a contradiction which indicates that there is no solution.
Example
Solve the following system of equations.
[latex]\begin{array}{l}x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
Solution
The first equation is already solved for [latex]x[/latex], so can substitute the expression [latex]9-2y[/latex] for [latex]x[/latex] in the second equation:
[latex]\begin{array}{r}x+2y=13\hfill \\ \left(9 - 2y\right)+2y=13\hfill \\ 9+0y=13\hfill \\ 9=13\hfill \end{array}[/latex]
Clearly, this statement is a contradiction because [latex]9\ne 13[/latex]. Therefore, the system has no solution.
In the next video, we show another example of using substitution to solve a system that has no solution.
Try It
We have also seen linear equations in one variable and systems of equations in two variables that have an infinite number of solutions. In the next example, we will see what happens when you apply the substitution method to a system with an infinite number of solutions.
Example
Solve for [latex]x[/latex] and [latex]y[/latex].
[latex]\begin{array}{l}\,\,\,y=−0.5x\\9y=−4.5x\end{array}[/latex]
Solution
Substitute [latex]−0.5x[/latex] for [latex]y[/latex] in the second equation:
[latex]\begin{array}{r}9y=−4.5x\\9(−0.5x)=−4.5\,\,\,\\−4.5x=−4.5x\end{array}[/latex]
This is an identity, so there are an infinite number of solutions represented by [latex]y=-0.5x[/latex].
The solution can also be written as an ordered pair with [latex]y[/latex] written in terms of [latex]x[/latex]: [latex](x,-0.5x)[/latex].
Graphing can help us make sense of the system in the example above.
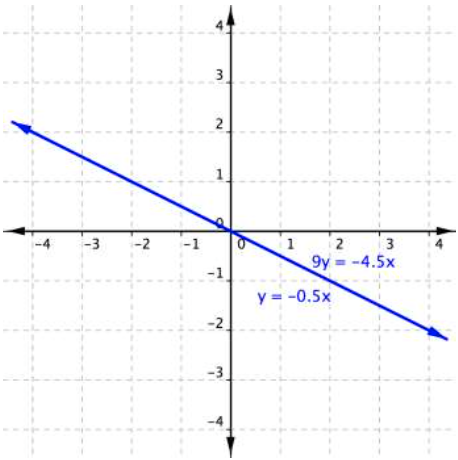
This system consists of two equations that both represent the same line; the two lines coincide. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions that lie on the line [latex]y=-0.5x[/latex].
Try It
The following video shows an example of solving a system that has an infinite number of solutions.
The following video shows an example of solving a system of equations that has no solutions.
Summary
The substitution method is one way of solving systems of equations. To use the substitution method, use one equation to find an expression for one of the variables in terms of the other variable. Then substitute that expression in place of that variable in the second equation. Then solve this equation as it will now have only one variable. Solving using the substitution method will yield one of three results: a single value for each variable within the system (indicating one solution), a contradiction (indicating no solutions), or an identity (indicating an infinite number of solutions that are represented by either equation).
