1.3.1: Factors and the Greatest Common Factor

Learning Outcomes

Determine which numbers are prime and composite
Find all the factors of a number
Find the prime factorization of a composite number
Find the greatest common factor of a composite number

Key words

Factor: A number that divides exactly into a natural number
Prime number: A number with exactly two factors, 1 and the number itself
Composite number: A number with more than two factors
Prime factorization: the product of prime numbers that equals a number
Greatest common factor: the largest number that divides exactly into two or more numbers

Factors

When we have the product of two numbers, we call the two numbers that are multiplied the factors of the number. We can see below that 8 and 9 are factors of 72: 8 and 9 divide exactly into 72.

The image shows the equation 8 times 9 equals 72. The 8 and 9 are labeled as factors and the 72 is labeled product.

Factors

If [latex]a\cdot b=m[/latex], then [latex]a\text{ and }b[/latex] are factors of [latex]m[/latex], and [latex]m[/latex] is the product of [latex]a\text{ and }b[/latex].

It can be useful to determine all of the factors of a number as it can help us solve many kinds of problems.

For example, suppose a choreographer is planning a dance for a ballet recital. There are [latex]24[/latex] dancers, and for a certain scene, the choreographer wants to arrange the dancers in groups of equal sizes on stage.

In how many ways can the dancers be put into groups of equal size? Answering this question is the same as identifying the factors of [latex]24[/latex]. The table below summarizes the different ways that the choreographer can arrange the dancers.

Number of Groups	Dancers per Group	Total Dancers
[latex]1[/latex]	[latex]24[/latex]	[latex]1\cdot 24=24[/latex]
[latex]2[/latex]	[latex]12[/latex]	[latex]2\cdot 12=24[/latex]
[latex]3[/latex]	[latex]8[/latex]	[latex]3\cdot 8=24[/latex]
[latex]4[/latex]	[latex]6[/latex]	[latex]4\cdot 6=24[/latex]
[latex]6[/latex]	[latex]4[/latex]	[latex]6\cdot 4=24[/latex]
[latex]8[/latex]	[latex]3[/latex]	[latex]8\cdot 3=24[/latex]
[latex]12[/latex]	[latex]2[/latex]	[latex]12\cdot 2=24[/latex]
[latex]24[/latex]	[latex]1[/latex]	[latex]24\cdot 1=24[/latex]

What patterns do you see in the table above? Did you notice that the number of groups times the number of dancers per group is always [latex]24?[/latex] This makes sense, since there are always [latex]24[/latex] dancers.

You may notice another pattern if you look carefully at the first two columns. These two columns contain the exact same set of numbers—but in reverse order. They are mirrors of one another, and in fact, both columns list all of the factors of [latex]24[/latex], which are:

[latex]1,2,3,4,6,8,12,24[/latex]

We can find all the factors of any natural number by systematically dividing the number by each natural number, starting with [latex]1[/latex]. If the quotient is also a natural number (meaning there is no remainder when you divide), then the divisor and the quotient are factors of the number. We can stop when the quotient becomes smaller than the divisor.

Find all the factors of a counting number

Divide the number by each of the natural numbers, in order, until the quotient is smaller than the divisor.
- If the quotient is a natural number, the divisor and quotient are a pair of factors.
- If the quotient is not a natural number, the divisor is not a factor.
List all the factor pairs.
Write all the factors in order from smallest to largest.

example

Find all the factors of [latex]72[/latex].

Solution:
Divide [latex]72[/latex] by each of the natural numbers starting with [latex]1[/latex]. If the quotient is a whole number, the divisor and quotient are a pair of factors.

The figure shows a table with ten rows and four columns. The first row is a header row and labels the rows
The next line would have a divisor of [latex]9[/latex] and a quotient of [latex]8[/latex]. The quotient would be smaller than the divisor, so we stop. If we continued, we would end up only listing the same factors again in reverse order. Listing all the factors from smallest to largest, we have [latex]1,2,3,4,6,8,9,12,18,24,36,\text{ and }72[/latex].

try it

In the following video we show how to find all the factors of [latex]30[/latex].

Prime and Composite Numbers

Some numbers, like [latex]72[/latex], have many factors. Other numbers, such as [latex]7[/latex], have only two factors: [latex]1[/latex] and the number. A number with only two factors is called a prime number. A number with more than two factors is called a composite number. The number [latex]1[/latex] is neither prime nor composite. It has only one factor, itself.

Prime Numbers and Composite Numbers

A prime number is a counting number greater than [latex]1[/latex] whose only factors are [latex]1[/latex] and itself.
A composite number is a counting number that is not prime.

The table below lists the counting numbers from [latex]2[/latex] through [latex]20[/latex] along with their factors. The highlighted numbers are prime, since each has only two factors.

Factors of the counting numbers from [latex]2[/latex] through [latex]20[/latex], with prime numbers highlighted

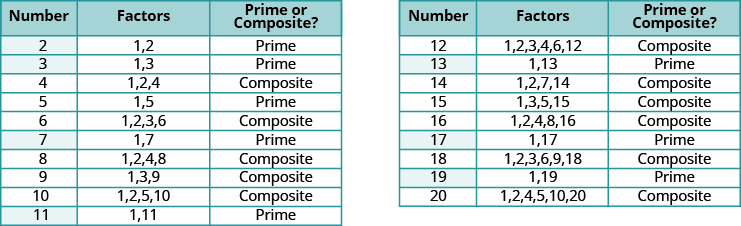
This figure shows a table with twenty rows and three columns. The first row is a header row. It labels the columns as
The prime numbers less than [latex]20[/latex] are [latex]2,3,5,7,11,13,17,\text{and }19[/latex]. There are many larger prime numbers too. In order to determine whether a number is prime or composite, we need to see if the number has any factors other than [latex]1[/latex] and itself. To do this, we can test each of the smaller prime numbers in order to see if it is a factor of the number. If none of the prime numbers are factors, then that number is also prime.

Determine if a number is prime

Test each of the primes, in order, to see if it is a factor of the number.
Start with [latex]2[/latex] and stop when the quotient is smaller than the divisor or when a prime factor is found.
If the number has a prime factor, then it is a composite number. If it has no prime factors, then the number is prime.

example

Identify each number as prime or composite:

[latex]83[/latex]
[latex]77[/latex]

Show Solution

Prime	Test	Factor of [latex]83?[/latex]
[latex]2[/latex]	Last digit of [latex]83[/latex] is not [latex]0,2,4,6,\text{or }8[/latex].	No.
[latex]3[/latex]	[latex]8+3=11[/latex], and [latex]11[/latex] is not divisible by [latex]3[/latex].	No.
[latex]5[/latex]	The last digit of [latex]83[/latex] is not [latex]5[/latex] or [latex]0[/latex].	No.
[latex]7[/latex]	[latex]83\div 7=(11.857\dots)[/latex]	No.
[latex]11[/latex]	[latex]83\div 11=(7.545\dots)[/latex]	No.

Prime	Test	Factor of [latex]77?[/latex]
[latex]2[/latex]	Last digit is not [latex]0,2,4,6,\text{or }8[/latex].	No.
[latex]3[/latex]	[latex]7+7=14[/latex], and [latex]14[/latex] is not divisible by [latex]3[/latex].	No.
[latex]5[/latex]	the last digit is not [latex]5[/latex] or [latex]0[/latex].	No.
[latex]7[/latex]	[latex]77\div 11=7[/latex]	Yes.

try it

In the following video we show more examples of how to determine whether a number is prime or composite.

Prime Factorization

Prime numbers have only two factors, the number [latex]1[/latex] and the prime number itself. Composite numbers have more than two factors, and every composite number can be written as a unique product of primes. This is called the prime factorization of a number. When we write the prime factorization of a number, we are rewriting the number as a product of primes. Finding the prime factorization of a composite number will help you later in this course.

Prime Factorization

The prime factorization of a number is the product of prime numbers that equals the number.

You may want to refer to the following list of prime numbers less than [latex]50[/latex] as you work through this section.

[latex]2,3,5,7,11,13,17,19,23,29,31,37,41,43,47[/latex]

Prime Factorization Using the Factor Tree Method

One way to find the prime factorization of a number is to make a factor tree. We start by writing the number, and then writing it as the product of two factors. We write the factors below the number and connect them to the number with a small line segment—a “branch” of the factor tree.

If a factor is prime, we circle it (like a bud on a tree), as we cannot factor that “branch” any further. If a factor is not prime, we repeat this process, writing it as the product of two factors and adding new branches to the tree.

We continue until all the branches end with a prime. When the factor tree is complete, the circled primes give us the prime factorization.

For example, let’s find the prime factorization of [latex]36[/latex]. We can start with any factor pair such as [latex]3[/latex] and [latex]12[/latex]. We write [latex]3[/latex] and [latex]12[/latex] below [latex]36[/latex] with branches connecting them.

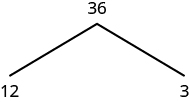
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end.
The factor [latex]3[/latex] is prime, so we circle it. The factor [latex]12[/latex] is composite, so we need to find its factors. Let’s use [latex]3[/latex] and [latex]4[/latex]. We write these factors on the tree under the [latex]12[/latex].

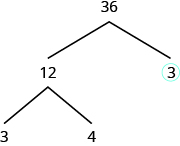
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end. Two more branches are splitting out from under 12. The right branch has the number 4 at the end and the left branch has the number 3 at the end.
The factor [latex]3[/latex] is prime, so we circle it. The factor [latex]4[/latex] is composite, and it factors into [latex]2\cdot 2[/latex]. We write these factors under the [latex]4[/latex]. Since [latex]2[/latex] is prime, we circle both [latex]2\text{s}[/latex].

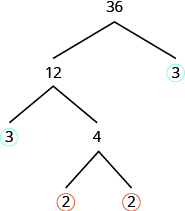
The prime factorization is the product of the circled primes. We generally write the prime factorization in order from least to greatest.

[latex]2\cdot 2\cdot 3\cdot 3[/latex]

In cases like this, where some of the prime factors are repeated, we can write prime factorization in exponential form.

[latex]\begin{array}{c}2\cdot 2\cdot 3\cdot 3\\ \\ {2}^{2}\cdot {3}^{2}\end{array}[/latex]

Note that we could have started our factor tree with any factor pair of [latex]36[/latex]. We chose [latex]12[/latex] and [latex]3[/latex], but the same result would have been the same if we had started with [latex]2[/latex] and [latex]18,4[/latex] and [latex]9,\text{or}6\text{and}6[/latex].

Find the prime factorization of a composite number using the tree method

Find any factor pair of the given number, and use these numbers to create two branches.
If a factor is prime, that branch is complete. Circle the prime.
If a factor is not prime, write it as the product of a factor pair and continue the process.
Write the composite number as the product of all the circled primes.

example

Find the prime factorization of [latex]48[/latex] using the factor tree method.

Solution:

We can start our tree using any factor pair of [latex]48[/latex]. Let’s use [latex]2\text{ and }24[/latex]. We circle the [latex]2[/latex] because it is prime and so that branch is complete.
Now we will factor [latex]24[/latex]. Let’s use [latex]4\text{ and }6[/latex].
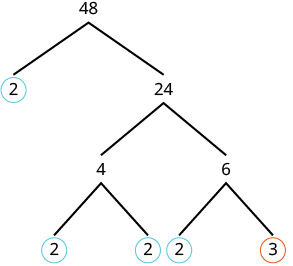Neither factor is prime, so we do not circle either.We factor the [latex]4[/latex], using [latex]2\text{ and }2[/latex]. We factor [latex]6\text{, using }2\text{ and }3[/latex]. We circle the [latex]2\text{s and the }3[/latex] since they are prime. Now all of the branches end in a prime.
Write the product of the circled numbers.	[latex]2\cdot 2\cdot 2\cdot 2\cdot 3[/latex]
Write in exponential form.	[latex]{2}^{4}\cdot 3[/latex]

Check this on your own by multiplying all the factors together. The result should be [latex]48[/latex].

try it

The following video shows how to find the prime factorization of [latex]60[/latex] using the factor tree method.

example

Find the prime factorization of [latex]84[/latex] using the factor tree method.

Show Solution

try it

Finding the Greatest Common Factor

The greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, [latex]4[/latex] is the GCF of [latex]16[/latex] and [latex]20[/latex] because it is the largest number that divides evenly into both [latex]16[/latex] and [latex]20[/latex].

Greatest Common Factor

The greatest common factor (GCF) of two or more natural numbers is the largest natural number that is a factor of all the numbers.

We will show how to find the greatest common factor of two numbers.

Let’s first find the greatest common factor (GCF) of two whole numbers. The GCF of two natural numbers is the greatest natural number that is a factor of both of the numbers. Take the numbers [latex]50[/latex] and [latex]30[/latex].

[latex]\begin{array}{l}50=10\cdot5\\30=10\cdot3\end{array}[/latex]

Their greatest common factor is [latex]10[/latex], since [latex]10[/latex] is the greatest factor that both numbers have in common.

To find the GCF of larger numbers, you can factor each number to find their prime factors, identify the prime factors they have in common, and then multiply those together.

example

Find the greatest common factor of [latex]24[/latex] and [latex]36[/latex].

Solution

Step 1: Factor each coefficient into primes. Write all variables with exponents in expanded form.	Factor [latex]24[/latex] and [latex]36[/latex].
Step 2: List all factors–matching common factors in a column.
In each column, circle the common factors.	Circle the [latex]2, 2[/latex], and [latex]3[/latex] that are shared by both numbers.
Step 3: Bring down the common factors that all expressions share.	Bring down the [latex]2, 2, 3[/latex] and then multiply.
Step 4: Multiply the factors.		The GCF of [latex]24[/latex] and [latex]36[/latex] is [latex]12[/latex].

Notice that since the GCF is a factor of both numbers, [latex]24[/latex] and [latex]36[/latex] can be written as multiples of [latex]12[/latex].

[latex]\begin{array}{c}24=12\cdot 2\\ 36=12\cdot 3\end{array}[/latex]

Example

Find the greatest common factor of [latex]210[/latex] and [latex]168[/latex].

Show Solution

Because the GCF is the product of the prime factors that these numbers have in common, we know that it is a factor of both numbers. (If you want to test this, go ahead and divide both [latex]210[/latex] and[latex]168[/latex] by [latex]42[/latex]—they are both exactly divisible by this number!)

The video that follows shows another example of finding the greatest common factor of two natural numbers.

try it

The Greatest Common Factor of More Than Two Numbers

The greatest common factor of more than two numbers is found in a similar way. The prime numbers used for the GCF must be factor triple, quadruples etc.

Example

Find the greatest common factor of [latex]48, 36, \text{and }30[/latex].

Solution

First write the prime factorization for each number:

[latex]48=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3[/latex]

[latex]36=2\cdot 2\cdot 3\cdot 3[/latex]

[latex]30=2\cdot 3\cdot 5[/latex]

Now line up the prime factorizations into columns of the same prime, determine which primes are common to all 3 numbers, multiply these primes to find the GFC.

Try It

Find the greatest common factor of [latex]77, 154, 63, \text{and }126[/latex].

Show Answer

Chapter 1: Real Numbers and Sets