Chapter 6: Linear Equations in Two Variables

6.3.2: Graphing Vertical and Horizontal Lines

Learning Objectives

Type your learning objectives here.

  • Graph a vertical line
  • Give the equation of a vertical line
  • Graph a horizontal line
  • Give the equation of a horizontal line

Key words

Type your key takeaways here.

  • vertical line: a line that runs in the same direction as the [latex]y[/latex]-axis
  • horizontal line: a line that runs in the same direction as the [latex]x[/latex]-axis

Vertical and Horizontal Lines

Consider the vertical line graphed in figure 1, and the solution table that goes with it.

 

x=2

[latex]x[/latex] [latex]y[/latex]
2 -3
2 -1
2 0
2 1
2  3

 

 

No matter the value of [latex]y[/latex], [latex]x=2[/latex]. So [latex]x=2[/latex] is the equation of the line.

Figure 1.

VERTICAL LINES

The equation of a vertical line is given as: [latex]x=c[/latex] where c is a constant.

To graph the equation on the coordinate plane, we need both [latex]x[/latex] and [latex]y[/latex] variables in the equation. Therefore, the equation of the vertical line in two variables is: [latex]x+0y=c[/latex] where c is a constant.

Consider the horizontal line graphed in figure 2, and the solution table that goes with it.

 

y=3

[latex]x[/latex] [latex]y[/latex]
-3 3
-1 3
0 3
2 3
4  3

 

 

No matter the [latex]x[/latex]-value, the [latex]y[/latex]-value is always 3. So the equation of the line is [latex]y=3[/latex].

Figure 2.

HORIZONTAL LINES

The equation of a horizontal line is given as: [latex]y=c[/latex] where c is a constant.

To graph the equation on the coordinate plane, we need both [latex]x[/latex] and [latex]y[/latex] variables in the equation. Therefore, the equation of the horizontal line in two variables is [latex]0x+y=c[/latex].

Suppose we want to graph a the lines with equations [latex]x+0y=-3[/latex] and [latex]0x+y=-2[/latex].

The following points satisfy the first equation: [latex]\left(-3,-5\right),\left(-3,1\right),\left(-3,3\right)[/latex], and [latex]\left(-3,5\right)[/latex]. We can plot the points. Notice that all of the [latex]x[/latex]–coordinates are the same and we find a vertical line through [latex]x=-3[/latex].

The following points satisfy the second equation: [latex]\left(-2,-2\right),\left(0,-2\right),\left(3,-2\right)[/latex], and [latex]\left(5,-2\right)[/latex]. The graph is a horizontal line through [latex]y=-2[/latex]. Notice that all of the [latex]y[/latex]–coordinates are the same.

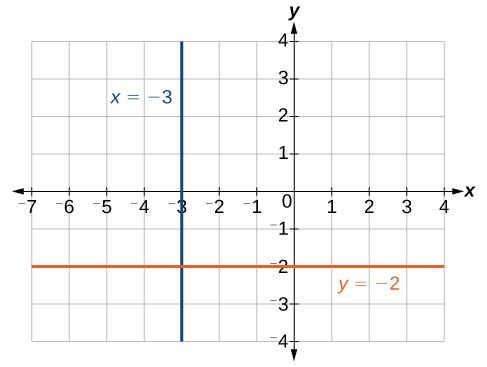Coordinate plane with the x-axis ranging from negative 7 to 4 and the y-axis ranging from negative 4 to 4. The function y = negative 2 and the line x = negative 3 are plotted.x = −3 is a vertical line.
y = −2 is a horizontal line.

try it

Use an online graphing tool to graph the following:

  1. A horizontal line that passes through the point (-5,2)
  2. A vertical line that passes through the point (3,3)


Example

Find the equation of the line passing through the given points: [latex]\left(1,-3\right)[/latex] and [latex]\left(1,4\right)[/latex].

Solution

The [latex]x[/latex]–coordinate of both points is 1. Therefore, we have a vertical line: [latex]x=1[/latex].

Try It

Find the equation of the line passing through [latex]\left(-5,2\right)[/latex] and [latex]\left(2,2\right)[/latex].

 

Privacy Policy