1.3.2: Multiples and the Least Common Multiple

Learning Objectives

Identify multiples of whole numbers
Find the least common multiple by listing multiples
Find the least common multiple of two numbers by prime factorization

Key words

Multiple: the product of a whole number and a natural number
Common multiple: a number that is a multiple of two or more numbers
Least common multiple: the smallest number that is a multiple of two or more numbers

Identifying Multiples of a Number

Annie is counting the shoes in her closet. The shoes are matched in pairs, so she doesn’t have to count each one. She counts by twos: $2,4,6,8,10,12$ . She has $12$ shoes in her closet.

The numbers $2,4,6,8,10,12$ are called multiples of $2$ . Multiples of $2$ can be written as the product of a natural number and $2$ . The first six multiples of $2$ are given below.

$\begin{array}{l}1\cdot 2=2\\ 2\cdot 2=4\\ 3\cdot 2=6\\ 4\cdot 2=8\\ 5\cdot 2=10\\ 6\cdot 2=12\end{array}$

A multiple of a number is the product of the number and a counting number. So a multiple of $3$ would be the product of a counting number and $3$ . Below are the first six multiples of $3$ .

$\begin{array}{l}1\cdot 3=3\\ 2\cdot 3=6\\ 3\cdot 3=9\\ 4\cdot 3=12\\ 5\cdot 3=15\\ 6\cdot 3=18\end{array}$

We can find the multiples of any number by continuing this process. The table below shows the multiples of $2$ through $9$ for the first twelve counting numbers.

Counting Number	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$12$
$\text{Multiples of }2$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	$16$	$18$	$20$	$22$	$24$
$\text{Multiples of }3$	$3$	$6$	$9$	$12$	$15$	$18$	$21$	$24$	$27$	$30$	$33$	$36$
$\text{Multiples of }4$	$4$	$8$	$12$	$16$	$20$	$24$	$28$	$32$	$36$	$40$	$44$	$48$
$\text{Multiples of }5$	$5$	$10$	$15$	$20$	$25$	$30$	$35$	$40$	$45$	$50$	$55$	$60$
$\text{Multiples of }6$	$6$	$12$	$18$	$24$	$30$	$36$	$42$	$48$	$54$	$60$	$66$	$72$
$\text{Multiples of }7$	$7$	$14$	$21$	$28$	$35$	$42$	$49$	$56$	$63$	$70$	$77$	$84$
$\text{Multiples of }8$	$8$	$16$	$24$	$32$	$40$	$48$	$56$	$64$	$72$	$80$	$88$	$96$
$\text{Multiples of }9$	$9$	$18$	$27$	$36$	$45$	$54$	$63$	$72$	$81$	$90$	$99$	$108$

Multiple of a Number

A number is a multiple of $n$ if it is the product of a natural number and $n$ .

Recognizing the patterns for multiples will be helpful to you as you continue in this course.

Finding the Least Common Multiple of Two Numbers

One of the reasons we find multiples and primes is to use them to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of $10$ and $25$ . We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.

$\begin{array}{c}10\text{ : }10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110\ldots \hfill \\ 25\text{ : }25, 50,75, 100, 125\ldots \hfill \end{array}$

We see that $50$ and $100$ appear in both lists. They are common multiples of $10$ and $25$ . We would find more common multiples if we continued the list of multiples for each.

The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of $10$ and $25$ is $50$ .

Find the least common multiple (LCM) of two numbers by listing multiples

List the first several multiples of each number.
Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
Look for the smallest number that is common to both lists.
This number is the LCM.

example

Find the LCM of $15$ and $20$ by listing multiples.

Solution:
List the first several multiples of $15$ and of $20$ . Identify the first common multiple.

$\begin{array}{l}\text{15: }15,30,45,60,75,90,105,120\hfill \\ \text{20: }20,40,60,80,100,120,140,160\hfill \end{array}$

The smallest number to appear on both lists is $60$ , so $60$ is the least common multiple of $15$ and $20$ .

Notice that $120$ is on both lists, too. It is a common multiple, but it is not the least common multiple.

try it

In the next video we show an example of how to find the Least Common Multiple by listing multiples of each number.

Prime Factors Method

Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of $12$ and $18$ .

We start by finding the prime factorization of each number.

$12=2\cdot 2\cdot 318=2\cdot 3\cdot 3$

Then we write each number as a product of primes, matching primes vertically when possible.

$\begin{array}{l}12=2\cdot 2\cdot 3\hfill \\ 18=2\cdot 3\cdot 3\end{array}$

Now we bring down a single prime from each column. The LCM is the product of these primes.

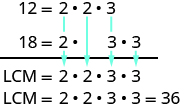
Notice that the prime factors of $12$ and the prime factors of $18$ are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that $36$ is the least common multiple.

Find the LCM using the prime factors method

Find the prime factorization of each number.
Write each number as a product of primes, matching primes vertically when possible.
Bring down a single prime from each column.
Multiply the factors to get the LCM.

example

Find the LCM of $15$ and $18$ using the prime factors method.

Show Solution

Solution:

Write each number as a product of primes.
Write each number as a product of primes, matching primes vertically when possible.
Bring down a single primes from each column.
Multiply the factors to get the LCM.	$\text{LCM}=2\cdot 3\cdot 3\cdot 5$ The LCM of $15\text{ and }18\text{ is } 90$ .

try it

example

Find the LCM of $50$ and $100$ using the prime factors method.

Show Solution

Solution:

Write the prime factorization of each number.	$50=2\cdot{5}\cdot{5}\quad\quad\quad{100=2\cdot{2}\cdot{5}\cdot{5}}$
Write each number as a product of primes, matching primes vertically when possible.	$50=\quad{2\cdot{5}\cdot{5}}$ $100=2\cdot{2}\cdot{5}\cdot{5}$
Bring down the primes in each column.
Multiply the factors to get the LCM.	$\text{LCM}=2\cdot 2\cdot 5\cdot 5$ The LCM of $50\text{ and } 100\text{ is } 100$ .

try it

In the next video we show how to find the Least Common Multiple by using prime factorization.

Finding the Least Common Multiple of More Than Two Numbers

The prime factorization method can be applied to more than two numbers.

Example

Find the least common multiple of $12, 20, \text{and }35.$

Solution

First write the prime factorization of each number:

$12=2\cdot 2\cdot 3$

$20=2\cdot 2\cdot 5$

$35=5\cdot 7$

Now line them up in matching columns, bring down a single prime from each, and multiply the prime factors:

LCM

Examples

Find the least common multiple of $42, 60, 14,\text{and }36$ .

Solution

First write the prime factorization of each number:

$42=2\cdot 3\cdot 7$

$60=2\cdot 2\cdot 3\cdot 5$

$14=2\cdot 7$

$36=2\cdot 2\cdot 3\cdot 3$

Now line them up in matching columns, bring down a single prime from each, and multiply the prime factors:

LCM example

Try It

Find the least common multiple of $14, 22, 48$ .

Show Answer

$14=2\cdot 7$

$22=2\cdot 11$

$48=2\cdot 2\cdot 2\cdot 2\cdot 3$

$\text{LCM }=3696$

Chapter 1: Real Numbers and Sets