Learning Objectives
- Identify a fraction as proper or improper
- Find equivalent fractions
- Simplify fractions
Key words
- Fraction: a rational number
- Numerator: the integer on top of a fraction
- Denominator: the integer on the bottom of a fraction
- Proper fraction: a fraction whose value lies between 0 and 1
- Improper fraction: a fraction whose value is greater than or equal to 1
- Equivalent fractions: two or more fractions with equal value
- Simplified fraction: a fraction that has no common factors (other than 1) in the numerator and denominator
Often in life, whole amounts are not exactly what we need. A baker must use a little more than a cup of milk or part of a teaspoon of salt. Similarly a carpenter might need less than a foot of wood and a painter might use part of a gallon of paint. In the next section, we will learn about numbers that describe parts of a whole. These numbers, called fractions, are very useful both in algebra and in everyday life. We have also seen these types of numbers in the real number system. They are called rational numbers. The set of rational numbers is the set of numbers that can be written as a fraction of two integers. [latex]\mathbb{Q}=\,\left\{\dfrac{m}{n}\normalsize \;\large\vert\;\normalsize\,m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex].
RATIONAL NUMBERS
A rational number (also called a fraction) is written [latex]\frac{a}{b}[/latex], where [latex]a[/latex] and [latex]b[/latex] are integers and [latex]b \neq 0[/latex]. In a fraction, [latex]a[/latex] is called the numerator and [latex]b[/latex] is called the denominator.
Rational numbers are also called fractions. The top number is referred to as the numerator of the fraction and the bottom number is the denominator. When the fraction is positive, and the numerator is smaller than the denominator, the fraction is a proper fraction. This means that the fraction is less than [latex]1[/latex] and represents part of a whole. For example, [latex]\frac{2}{3}[/latex] is a proper fraction since [latex]2 \lt 3[/latex]. [latex]\frac{2}{3}[/latex] is part of a whole. On the other hand, when the numerator is greater than or equal to the denominator, the fraction is said to be improper. The fractions [latex]\frac{7}{4}[/latex] and [latex]\frac{5}{5}[/latex] are examples of improper fractions because their numerators are greater than or equal to their denominators. Improper fractions represent numbers that are greater than or equal to 1; they are a whole or larger.
Example
Determine of the fraction is proper or improper:
- [latex]\frac{2}{5}[/latex] Proper since [latex]2\lt 5[/latex]
- [latex]\frac{3}{4}[/latex] Proper since [latex]3\lt 4[/latex]
- [latex]\frac{7}{2}[/latex] Improper since [latex]7\geq 2[/latex]
- [latex]\frac{9}{9}[/latex] Improper since [latex]9\geq 9[/latex]
Try It
Determine of the fraction is proper or improper:
- [latex]\frac{6}{5}[/latex]
- [latex]\frac{8}{9}[/latex]
- [latex]\frac{7}{7}[/latex]
- [latex]\frac{6}{9}[/latex]
Equivalent Fractions
If Anwar eats [latex]\frac{1}{2}[/latex] of a pizza and Bobby eats [latex]\frac{2}{4}[/latex] of the pizza, have they eaten the same amount of pizza? In other words, does [latex]\frac{1}{2}=\frac{2}{4}[/latex]? We can use fraction tiles to find out whether Anwar and Bobby have eaten equivalent parts of the pizza.
Equivalent Fractions
Equivalent fractions are fractions that have the same value.
Fraction tiles serve as a useful model of equivalent fractions. You may want to use fraction tiles to do the following activity. Or you might make a copy of the fraction tiles shown earlier and extend it to include eighths, tenths, and twelfths.
Start with a [latex]\frac{1}{2}[/latex] tile. How many fourths equal one-half? How many of the [latex]\frac{1}{4}[/latex] tiles exactly cover the [latex]\frac{1}{2}[/latex] tile?

Since two [latex]\frac{1}{4}[/latex] tiles cover the [latex]\frac{1}{2}[/latex] tile, we see that [latex]\frac{2}{4}[/latex] is the same as [latex]\frac{1}{2}[/latex], or [latex]\frac{2}{4}=\frac{1}{2}[/latex].
How many of the [latex]\frac{1}{6}[/latex] tiles cover the [latex]\frac{1}{2}[/latex] tile?

Since three [latex]\frac{1}{6}[/latex] tiles cover the [latex]\frac{1}{2}[/latex] tile, we see that [latex]\frac{3}{6}[/latex] is the same as [latex]\frac{1}{2}[/latex].
So, [latex]\frac{3}{6}=\frac{1}{2}[/latex]. The fractions are equivalent fractions.
Example
Use fraction tiles to find equivalent fractions. Show your result with a figure.
- How many eighths [latex]\left( \frac{1}{8} \right)[/latex] equal one-half [latex]\left( \frac{1}{2} \right)[/latex]?
- How many tenths [latex]\left( \frac{1}{10} \right)[/latex] equal one-half [latex]\left( \frac{1}{2} \right)[/latex]?
- How many twelfths [latex]\left( \frac{1}{12} \right)[/latex] equal one-half [latex]\left( \frac{1}{2}\right)[/latex]?
Solution
1. It takes four [latex]\frac{1}{8}[/latex] tiles to exactly cover the [latex]\frac{1}{2}[/latex] tile, so [latex]\frac{4}{8}=\frac{1}{2}[/latex].

2. It takes five [latex]\frac{1}{10}[/latex] tiles to exactly cover the [latex]\frac{1}{2}[/latex] tile, so [latex]\frac{5}{10}=\frac{1}{2}[/latex].

3. It takes six [latex]\frac{1}{12}[/latex] tiles to exactly cover the [latex]\frac{1}{2}[/latex] tile, so [latex]\frac{6}{12}=\frac{1}{2}[/latex].

Suppose you had tiles marked [latex]\frac{1}{20}[/latex]. How many of them would it take to equal [latex]\frac{1}{2}[/latex]? Are you thinking ten tiles? If you are, you’re right, because [latex]\frac{10}{20}=\frac{1}{2}[/latex].
We have shown that [latex]\frac{1}{2},\frac{2}{4},\frac{3}{6},\frac{4}{8},\frac{5}{10},\frac{6}{12}[/latex], and [latex]\frac{10}{20}[/latex] are all equivalent fractions.
Try it
Finding Equivalent Fractions
We used fraction tiles to show that there are many fractions equivalent to [latex]\frac{1}{2}[/latex]. For example, [latex]\frac{2}{4},\frac{3}{6}[/latex], and [latex]\frac{4}{8}[/latex] are all equivalent to [latex]\frac{1}{2}[/latex]. When we lined up the fraction tiles, it took four of the [latex]\frac{1}{8}[/latex] tiles to make the same length as a [latex]\frac{1}{2}[/latex] tile. This showed that [latex]\frac{4}{8}=\frac{1}{2}[/latex]. See the previous example.
We can show this with pizzas, too. Image (a) shows a single pizza, cut into two equal pieces with [latex]{\frac{1}{2}}[/latex] shaded. Image (b) shows a second pizza of the same size, cut into eight pieces with [latex]{\frac{4}{8}}[/latex] shaded.
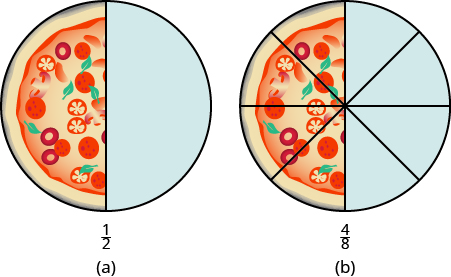
This is another way to show that [latex]\frac{1}{2}[/latex] is equivalent to [latex]\frac{4}{8}[/latex].
How can we use mathematics to change [latex]\frac{1}{2}[/latex] into [latex]\frac{4}{8}[/latex]? How could you take a pizza that is cut into two pieces and cut it into eight pieces? You could cut each of the two larger pieces into four smaller pieces! The whole pizza would then be cut into eight pieces instead of just two. Mathematically, what we’ve described could be written as:
[latex]\frac{1\cdot\color{blue}{4}}{2\cdot\color{blue}{4}}=\frac{4}{8}[/latex]
These models lead to the Equivalent Fractions Property, which states that if we multiply the numerator and denominator of a fraction by the same number, the value of the fraction does not change.
Equivalent Fractions Property
If [latex]a,b[/latex], and [latex]c[/latex] are numbers where [latex]b\ne 0[/latex] and [latex]c\ne 0[/latex], then
[latex]\frac{a}{b}=\frac{a\cdot c}{b\cdot c}[/latex]
When working with fractions, it is often necessary to express the same fraction in different forms. To find equivalent forms of a fraction, we can use the Equivalent Fractions Property. For example, consider the fraction one-half.
[latex]{\frac{1\cdot\color{blue}{3}}{2\cdot\color{blue}{3}}}={\frac{3}{6}}[/latex] so [latex]{\frac{1}{2}}={\frac{3}{6}}[/latex]
[latex]{\frac{1\cdot\color{blue}{2}}{2\cdot\color{blue}{2}}}={\frac{2}{4}}[/latex] so [latex]{\frac{1}{2}}={\frac{2}{4}}[/latex]
[latex]{\frac{1\cdot\color{blue}{10}}{2\cdot\color{blue}{10}}}={\frac{10}{20}}[/latex] so [latex]{\frac{1}{2}}={\frac{10}{20}}[/latex]
So, we say that [latex]\frac{1}{2},\frac{2}{4},\frac{3}{6}[/latex], and [latex]\frac{10}{20}[/latex] are equivalent fractions.
Example
Find three fractions equivalent to [latex]{\frac{2}{5}}[/latex].
Try it
Find three fractions equivalent to [latex]{\frac{3}{5}}[/latex].
Find three fractions equivalent to [latex]{\frac{4}{5}}[/latex].
When we add and subtract fractions, we often need to build fractions to create fractions with the same denominator. We build fractions by multiplying the numerator and denominator of the fraction by the same number (the equivalent fractions property).
Example
Find a fraction with a denominator of [latex]21[/latex] that is equivalent to [latex]{\frac{2}{7}}[/latex].
Try it
In the following video we show more examples of how to find an equivalent fraction given a specific denominator.
Positive and Negative Fractions
Rational numbers can be negative as well as positive. Being negative just means that they sit on the opposite side of zero from the positive version of the fraction.
For example, the fraction [latex]\frac{1}{2}[/latex] is located exactly half-way between [latex]0[/latex] and [latex]1[/latex] on the number line. The distance between [latex]0[/latex] and [latex]1[/latex] is split into two equal lengths and [latex]\frac{1}{2}[/latex] sits exactly one of the two equal lengths from zero.

[latex]-\frac{1}{2}[/latex] is the opposite of [latex]\frac{1}{2}[/latex] and lies on the opposite side of zero.
[latex]\frac{3}{2}[/latex] lies three half-units from zero, and [latex]-\frac{3}{2}[/latex] lies three half-units from zero on the negative side of the number line. Notice also, that [latex]\frac{1}{2}[/latex] lies between [latex]0[/latex] and [latex]1[/latex] so is a proper fraction, while [latex]\frac{3}{2}[/latex] is greater than or equal to [latex]1[/latex] so is an improper fraction.
Simplifying Fractions
In working with equivalent fractions, we saw that there are many ways to write fractions that have the same value, or represent the same part of the whole. How do we know which one to use? Most often, we’ll use the fraction that is in simplified form.
A fraction is considered simplified if there are no common factors, other than [latex]1[/latex], in the numerator and denominator. If a fraction does have common factors in the numerator and denominator, we can simplify the fraction to its simplified form by dividing the numerator and denominator by the common factors.
Simplified Fraction
A fraction is considered simplified if there are no common factors in the numerator and denominator.
For example,
- [latex]\frac{2}{3}[/latex] is simplified because, other than 1, there are no common factors of [latex]2[/latex] and [latex]3[/latex].
- [latex]\frac{10}{15}[/latex] is NOT simplified because [latex]5[/latex] is a common factor of [latex]10[/latex] and [latex]15[/latex].
We can use the Equivalent Fractions Property in reverse to simplify fractions. We rewrite the property to show both forms together.
Equivalent Fractions Property
If [latex]a,b,c[/latex] are integers where [latex]b\ne 0,c\ne 0[/latex], then
[latex]{\frac{a}{b}}={\frac{a\cdot c}{b\cdot c}}\text{ and }{\frac{a\cdot c}{b\cdot c}}={\frac{a}{b}}[/latex].
Notice that [latex]c[/latex] is a common factor in the numerator and denominator. Anytime we have a common factor in the numerator and denominator, we can divide the numerator and denominator by the common factor to remove it.
Simplifying a fraction.
- Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers.
- Simplify, using the equivalent fractions property, by dividing both the numerator and denominator by the common factor to remove it.
- Multiply any remaining factors.
Example
Simplify: [latex]\frac{10}{15}[/latex]
Solution:
To simplify the fraction, we look for any common factors in the numerator and the denominator.
| Notice that [latex]5[/latex] is a factor of both [latex]10[/latex] and [latex]15[/latex]. | [latex]\frac{10}{15}[/latex] |
| Factor the numerator and denominator. | [latex]\frac{2\cdot5}{3\cdot5}[/latex] |
| 5 is a common factor so divide the numerator and denominator by 5 to remove it. | [latex]\frac{2\cdot\color{red}{5}}{3\cdot\color{red}{5}}[/latex] |
| Simplify. | [latex]\frac{2}{3}[/latex] |
try it
Simplify the fractions:
1. [latex]\frac{14}{21}[/latex] 2. [latex]\frac{20}{50}[/latex] 3. [latex]\frac{12}{24}[/latex] 4. [latex]\frac{8}{28}[/latex] 5. [latex]\frac{17}{17}[/latex]
To simplify a negative fraction, we use the same process as in the previous example. Remember to keep the negative sign.
Example
Simplify: [latex]-\frac{18}{24}[/latex]
Try it
Simplify the fractions:
1. [latex]-\frac{14}{21}[/latex] 2. [latex]-\frac{40}{50}[/latex] 3. [latex]-\frac{48}{24}[/latex] 4. [latex]-\frac{21}{28}[/latex] 5. [latex]-\frac{23}{23}[/latex]
Watch the following video to see another example of how to simplify a fraction.
After simplifying a fraction, it is always important to check the result to make sure that the numerator and denominator do not have any more factors in common. Remember, the definition of a simplified fraction: a fraction is considered simplified if there are no common factors in the numerator and denominator.
Example
Simplify: [latex]-\frac{56}{32}[/latex]
Sometimes it may not be easy to find common factors of the numerator and denominator. A good idea, then, is to factor the numerator and the denominator into prime numbers. Then divide out the common factors using the Equivalent Fractions Property.
Example
Simplify: [latex]\frac{210}{385}[/latex]
Try it
Simplify [latex]\frac{315}{675}[/latex]
Candela Citations
- Question ID: 146014, 146015, 146017, 146018, 146019. Authored by: Alyson Day. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex 1: Simplifying Fractions. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/tLgfPeecGe0. License: CC BY: Attribution
- Prealgebra. Authored by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757

