Learning Outcomes
- Define [latex]i[/latex] as the square root of -1
- Take the square root of a negative number
- Express imaginary numbers as [latex]bi[/latex] and complex numbers as [latex]a+bi[/latex]
- Simplify complex numbers to standard form
Key WORDS
- Rational numbers: the set of numbers that can be written as the ratio of two integers
- Irrational numbers: the set of numbers that can not be written as the ratio of two integers
- Real numbers: the set of numbers formed by the union of the set of rational numbers with the set of irrational numbers
- Imaginary numbers: the set of numbers formed from the square root of a negative real number
- Complex numbers: the set of numbers formed from a union of the set of real numbers and the set of imaginary numbers
- Standard form of a complex number: [latex]a+bi[/latex] where [latex]a[/latex] and [latex]b[/latex] are realnumbers
Square Root of a Negative Number
We have seen that taking the square root of a negative number is not possible in the Real number system. The set of real numbers is the union of the set of rational numbers and the set of irrational numbers and can be shown on a real number line. In order to take the square root of a negative number, we have to consider a new number system. But, we really need only one new number to start working with the square roots of negative numbers. That number is the square root of negative one, [latex]\sqrt{-1}[/latex] which we define to be the imaginary number [latex]i[/latex].
Another way of saying this is that [latex]{{i}^{2}}=-1[/latex]. This is because [latex]\sqrt{i^2}=i[/latex] and [latex]i=\sqrt{-1}[/latex] imply that [latex]\sqrt{i^2}=\sqrt{-1}[/latex] and, consequently, [latex]i^2=-1[/latex].
definition
[latex]{i}=\sqrt{-1}[/latex]
[latex]{{i}^{2}}=-1[/latex]
The number [latex]−1[/latex] allows us to work with roots of negative Real numbers, not just [latex]\sqrt{-1}[/latex]. There are two important square root rules to remember: [latex]\sqrt{-1}=i[/latex], and [latex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] for. We will use the latter rule to rewrite the square root of a negative number as the square root of a positive number times [latex]\sqrt{-1}[/latex], then rewrite[latex]\sqrt{-1}[/latex] as [latex]i[/latex].
Example
Simplify. [latex]\sqrt{-4}[/latex]
Solution
Use the rule [latex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex]\sqrt{-1}[/latex]:
[latex]\sqrt{-4}=\sqrt{4\cdot -1}=\sqrt{4}\sqrt{-1}[/latex]
Since [latex]4[/latex] is a perfect square [latex](4=2^{2})[/latex], we can simplify the square root of [latex]4[/latex]:
[latex]\sqrt{4}\sqrt{-1}=2\sqrt{-1}[/latex]
Use the definition of [latex]i[/latex] to rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex]:
[latex]2\sqrt{-1}=2i[/latex]
The answer is: [latex]\sqrt{-4}=2i[/latex]
Notice that [latex]\sqrt{-4}=2i[/latex] and not [latex]\pm2i[/latex]. This is because the radical sign [latex]\sqrt{}[/latex] represents the principal square root, which is always ≥ 0.
Example
Simplify. [latex]\sqrt{-9}[/latex]
Use the rule [latex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex]\sqrt{-1}[/latex]:
[latex]\sqrt{-9}=\sqrt{9\cdot -1}=\sqrt{9}\cdot\sqrt{-1}[/latex]
Since [latex]9[/latex] is a perfect square [latex](9=3^{2})[/latex], we can simplify the square root of [latex]9[/latex]:
[latex]\sqrt{9}\cdot\sqrt{-1}=3\cdot\sqrt{-1}[/latex]
Use the definition of [latex]i[/latex] to rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex]:
[latex]3\cdot\sqrt{-1}=3i[/latex]
The answer is: [latex]\sqrt{-9}=3i[/latex].
The only way to end up with a negative answer is if there is a negative sign in front of the radical.
Example
Simplify. [latex]-\sqrt{-64}[/latex]
Use the rule [latex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex]\sqrt{-1}[/latex]:
[latex]-\sqrt{-64}=-\sqrt{64\cdot -1}=-\sqrt{64}\sqrt{-1}[/latex]
Since [latex]64[/latex] is a perfect square [latex](64=8^{2})[/latex], we can simplify the square root of [latex]64[/latex]:
[latex]-\sqrt{64}\cdot\sqrt{-1}=-8\cdot\sqrt{-1}[/latex]
Use the definition of [latex]i[/latex] to rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex]:
[latex]-8\cdot\sqrt{-1}==-8i[/latex]
The answer is [latex]-\sqrt{-64}=-8i[/latex]
Rewriting the Square Root of a Negative Number as an imaginary number
- Find perfect squares within the radical.
- Rewrite the radical using the rule [latex]\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
- Rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex].
Try It
Rewrite the square roots as imaginary numbers:
- [latex]\sqrt{-49}[/latex]
- [latex]\sqrt{-81}[/latex]
- [latex]-\sqrt{-100}[/latex]
Imaginary Numbers
The set of imaginary numbers is defined as the set of all numbers of the form [latex]ai[/latex], where [latex]a[/latex] is a real number. [latex]2i,\; -7i,\; 9658i,\; \frac{3}{4}i,\; -\frac{9}{5}i,\; \sqrt{3}\,i[/latex] are all imaginary numbers. When there is a square root in front of the [latex]i[/latex], it is best to write the [latex]i[/latex] in front of the radical: [latex]i\sqrt{3}[/latex] so that it is obvious that the [latex]i[/latex] is not under the radical. In set builder notation, the set of imaginary numbers is defined as [latex]\{ai\; \large | \normalsize \;\;a\;\in\mathbb{R}\}[/latex]. The set of imaginary numbers is NOT a subset of the set of real numbers.
imaginary numbers
The set of imaginary numbers is defined as the set of all numbers of the form [latex]ai[/latex], where [latex]a[/latex] is a real number.
Imaginary numbers = [latex]\mathbb{I}=\{ai\; \large | \normalsize \;\;a\;\in\mathbb{R}\}[/latex]
The following video, shows more examples of how to use the imaginary number [latex]i[/latex] to simplify a square root with a negative radicand.
Examples
Write the square roots as imaginary numbers.
- [latex]\sqrt{-36}[/latex]
- [latex]\sqrt{-8}[/latex]
- [latex]-\sqrt{-16}[/latex]
- [latex]-\sqrt{-45}[/latex]
Solution
- [latex]\sqrt{-36}=\sqrt{36\cdot (-1)}=\sqrt{36}\cdot\sqrt{-1}=6i=[/latex]
- [latex]\sqrt{-8}=\sqrt{-1}\cdot\sqrt{8}=i\cdot\sqrt{4\cdot 2}=i\cdot\sqrt{4}\cdot\sqrt{2}=2i\sqrt{2}[/latex]
- [latex]-\sqrt{-16}=-\sqrt{16}\cdot\sqrt{-1}=-4i[/latex]
- [latex]-\sqrt{-45}=-\sqrt{-1}\cdot\sqrt{9}\cdot\sqrt{5}=-3i\sqrt{5}[/latex]
Try It
Write the square roots as imaginary numbers.
- [latex]\sqrt{-9}[/latex]
- [latex]\sqrt{-20}[/latex]
- [latex]-\sqrt{-100}[/latex]
- [latex]-\sqrt{-63}[/latex]
For example, [latex]\sqrt{-4}\cdot\sqrt{-9}\neq\sqrt{-4\cdot (-9)}[/latex], because [latex]\sqrt{-4}\cdot\sqrt{-9}=2i\cdot 3i=6i^2=6\cdot (-1)=-6[/latex] and [latex]\sqrt{-4\cdot (-9)}=\sqrt{36}=6[/latex].
Examples
Simplify:
- [latex]\sqrt{-4}\cdot\sqrt{-25}[/latex]
- [latex]\sqrt{-4\cdot-25}[/latex]
Solution
- [latex]\sqrt{-4}\cdot\sqrt{-25}=2i\cdot 5i=10i^2=10\cdot(-1)=-10[/latex]
- [latex]\sqrt{-4\cdot-25}=\sqrt{100}=10[/latex]
Try It
Simplify:
- [latex]\sqrt{-9}\cdot\sqrt{-36}[/latex]
- [latex]\sqrt{-9\cdot-36}[/latex]
- [latex]\sqrt{9\cdot-36}[/latex]
- [latex]-\sqrt{-9\cdot 36}[/latex]
Complex Numbers
The set of real numbers and the set of imaginary numbers have only one number in common: zero. Zero can be written as [latex]0[/latex] in the set of real numbers and [latex]0i[/latex] in the set of imaginary numbers. [latex]0i=0[/latex]. When we union the set of real numbers with the set of imaginary numbers, we get a new set of numbers called the complex numbers.
A complex number is expressed in standard form when written [latex]a+bi[/latex] where [latex]a[/latex] is the real part and [latex]bi[/latex] is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4i\sqrt{3}[/latex].
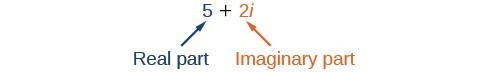
complex numbers
The set of complex numbers, [latex]\mathbb{C}[/latex], is the union of the set of real numbers and the set of imaginary numbers.
A complex number is in standard form when it is written in the form [latex]a+bi[/latex] where [latex]a[/latex] and [latex]b[/latex] are real numbers.
[latex]\mathbb{C}=\{a+bi\; \large | \normalsize \;\;a,b\;\in\mathbb{R}\}[/latex]
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number, while the square of a real number (either positive or negative) is a positive real number. Complex numbers are a combination of real and imaginary numbers.
| Complex Number | Real Part | Imaginary Part |
|---|---|---|
| [latex]3+7i[/latex] | [latex]3[/latex] | [latex]7i[/latex] |
| [latex]18–32i[/latex] | [latex]18[/latex] | [latex]−32i[/latex] |
| [latex]-\frac{3}{5}+i\sqrt{2}[/latex] | [latex]-\frac{3}{5}[/latex] | [latex]i\sqrt{2}[/latex] |
| [latex]\frac{\sqrt{2}}{2}-\frac{1}{2}i[/latex] | [latex]\frac{\sqrt{2}}{2}[/latex] | [latex]-\frac{1}{2}i[/latex] |
In a number with a radical as part of b, such as [latex]-\frac{3}{5}+i\sqrt{2}[/latex], [latex]i[/latex] should be written in front of the radical. Although writing this number as [latex]-\frac{3}{5}+\sqrt{2}i[/latex] is technically correct, it makes it much more difficult to tell whether [latex]i[/latex] is inside or outside of the radical. Putting it before the radical, as in [latex]-\frac{3}{5}+i\sqrt{2}[/latex], clears up any confusion.
By making [latex]b=0[/latex], any real number can be expressed as a complex number. The real number [latex]a[/latex] is written as [latex]a+0i[/latex] in complex form. Similarly, any imaginary number can be expressed as a complex number. By making [latex]a=0[/latex], any imaginary number [latex]bi[/latex] can be written as [latex]0+bi[/latex] in complex form.
| Number | Complex Form: [latex]a+bi[/latex] |
Real Part | Imaginary Part |
|---|---|---|---|
| [latex]17[/latex] | [latex]17+0i[/latex] | [latex]17[/latex] | [latex]0i[/latex] |
| [latex]−3i[/latex] | [latex]0–3i[/latex] | [latex]0[/latex] | [latex]−3i[/latex] |
These examples show that the set of real numbers is a subset of the complex numbers and the set of imaginary numbers is a subset of the complex numbers.
[latex]\mathbb{R}\subset\mathbb{C}\text{ and }\mathbb{I}\subset\mathbb{C}[/latex]
Example
Write [latex]83.6[/latex] as a complex number.
A complex number has the form [latex]a+bi[/latex].
Since [latex]83.6[/latex] is a real number, it is the real part (a) of the complex number [latex]a+bi[/latex].
A real number does not contain any imaginary parts, so the value of [latex]b[/latex] is [latex]0[/latex].
The answer is [latex]83.6+0i[/latex].
Example
Write [latex]−3i[/latex] as a complex number.
A complex number has the form [latex]a+bi[/latex].
Since [latex]−3i[/latex] is an imaginary number, it is the imaginary part [latex]bi[/latex] of the complex number [latex]a+bi[/latex].
This imaginary number has no real parts, so the value of [latex]a[/latex] is [latex]0[/latex].
The answer is [latex]0–3i[/latex].
Try It
Write the numbers as complex numbers in standard form:
- [latex]17[/latex]
- [latex]-\frac{7}{9}[/latex]
- [latex]-3i[/latex]
- [latex]\frac{\sqrt{2}}{5}i[/latex]
The video, shows more examples of how to write complex numbers.
Standard Form
The standard form of a complex number is [latex]a+bi[/latex]. So, [latex]\frac{5}{2}+\frac{3}{2}i[/latex] is a complex number written in standard form. However, if we used the common denominator to add the fractions, [latex]\frac{5+3i}{2}[/latex] is NOT in standard form. If a complex number is the numerator of a fraction, we can simplify the fraction to write the answer in standard form by splitting up the fractions.
Example
Simplify. [latex]\frac{5+3i}{2}[/latex]
Separate the fractions into a real part and an imaginary part:
[latex]\frac{5+3i}{2}=\frac{5}{2}+\frac{3i}{2}[/latex]
Simplify each fraction, if possible:
[latex]\frac{5}{2}+\frac{3i}{2}[/latex]
The answer is [latex]\frac{5+3i}{2}=\frac{5}{2}+\frac{3i}{2}[/latex].
Example
Simplify. [latex]\frac{2+3i}{4}[/latex]
Separate the fractions into a real part and an imaginary part:
[latex]\frac{2+3i}{4}=\frac{2}{4}+\frac{3i}{4}[/latex]
Simplify each fraction:
[latex]\frac{1}{2}+\frac{3i}{4}[/latex]
The answer is [latex]\frac{2+3i}{4}=\frac{1}{2}+\frac{3i}{4}[/latex].
Try It
Write in standard form:
- [latex]\frac{4+9i}{3}[/latex]
- [latex]\frac{-8+4i}{4}[/latex]
- [latex]\frac{7+3i}{9}[/latex]
The same technique can be used when there are radicals involved.
Examples
Simplify to standard form.
- [latex]\frac{6+i\sqrt{3}}{4}[/latex]
- [latex]\frac{12-4i\sqrt{5}}{2}[/latex]
- [latex]\frac{-24+\sqrt{-16}}{-8}[/latex]
- [latex]\frac{\sqrt{81}-\sqrt{-27}}{3}[/latex]
Candela Citations
- Write Number in the Form of Complex Numbers.. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning.. Provided by: Lumen Learning. Located at: https://youtu.be/mfoOYdDkuyY.. License: CC BY: Attribution
- Simplify Square Roots to Imaginary Numbers. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/LSp7yNP6Xxc. License: CC BY: Attribution
- Write Number in the form of a complex number. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/mfoOYdDkuyY. License: CC BY: Attribution
- 2.3: Complex Numbers. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
