Solving Linear Equations
Learning Objectives
- Determine whether or not an equation in one variable is defined as a linear equation
- Use the addition and subtraction property to solve a linear equation
- Use the multiplication and division property to solve a linear equation
KEY WORDS
- Equality: The state of two or more entities having the same value.
- Equation: a statement that two expressions are equal.
- Solution: a number or numbers that make an equation true.
- Equivalent equations: two or more equations that have identical solutions.
Linear Equations
An equation with just one variable is said to be linear when the highest power on the variable is [latex]1[/latex]. Remember that [latex]{x}^{1}[/latex] is equivalent to [latex]x[/latex], so any equation that can be simplified to [latex]ax+b=c[/latex] (where [latex]a,b,c[/latex] are real numbers) is a linear equation in one variable. For example, the equation [latex]2x+3=7, \;5x=7,\; -\frac{3}{4}x+\frac{7}{3}=\frac{6}{5}[/latex] are all linear equations because the highest power of [latex]x[/latex] is [latex]1[/latex]. On the other hand, the equation [latex]{x}^3+2{x}^2=4x-2[/latex] is NOT linear because the highest power of [latex]x[/latex] is [latex]3[/latex], not [latex]1[/latex].
EXAMPLE
Determine whether the equation is linear:
a) [latex]3x-7=6x+2[/latex]
b) [latex]{x}^{3}-5{x}^{2}=5x+6[/latex]
c) [latex]x(x+6)=8[/latex]
d) [latex]x-\frac{3}{8} =\frac{1}{2}[/latex]
Solution:
| a) [latex]3x-7=6x+2[/latex] | Yes, it is linear since the highest power of [latex]x[/latex] is [latex]1[/latex] |
| b) [latex]{x}^{3}-5{x}^{2}=5x+6[/latex] | No, it is NOT linear since the highest power of [latex]x[/latex] is [latex]3[/latex], not [latex]1[/latex] |
| c) [latex]x(x+6)=8[/latex] | Use the distributive property to simplify the left side of the equation: [latex]{x}^{2}+6x=8[/latex]. Now we can see that the equation is NOT linear since the highest power of [latex]x[/latex] is [latex]2[/latex], not [latex]1[/latex] |
| d) [latex]x-\frac{3}{8} =\frac{1}{2}[/latex] | Yes, it is linear since the highest power of [latex]x[/latex] is [latex]1[/latex] |
TRY IT
Determine whether the equation [latex]6x-7=8{x}^{2}+5[/latex] is linear.
TRY IT
Determine whether the equation [latex]\frac{4}{5}x+6=\frac{-7}{3}x[/latex] is linear.
The Addition and Subtraction Property of Equality
When an equation contains a variable such as [latex]x[/latex], this variable is considered an unknown value. In many cases, we can find the possible values for [latex]x[/latex] that would make the equation true. We can solve the equation for [latex]x[/latex].
For some equations like [latex]x + 3 =5[/latex] it is easy to guess the solution: the only possible value of [latex]x[/latex] is [latex]2[/latex], because [latex]2 + 3 = 5[/latex]. However, it becomes useful to have a process for finding solutions for unknowns as problems become more complex.
In order to solve an equation, we need to isolate the variable. Isolating the variable means rewriting an equivalent equation in which the variable is on one side of the equation and everything else is on the other side of the equation. The variable is an unknown quantity whose value we are trying to find. We have a solution when we reorganize the equation into the form [latex]x[/latex] = a constant.
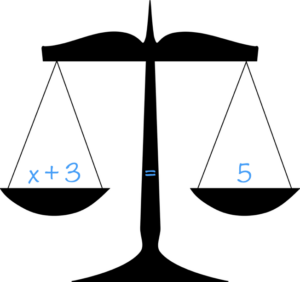
The second we add or subtract a “weight” to one side of the scale, it will become unbalanced. In order to right that balance, we must add or subtract the same “weight” to the other side of the sale.
To solve this equation for [latex]x[/latex], we need to isolate [latex]x[/latex] by removing the [latex]+3[/latex] from the left side of the equation. We do this this by “undoing” the addition of [latex]+3[/latex] by subtracting [latex]3[/latex]. In other words we use the inverse operation of addition, which is subtraction. But if we subtract [latex]3[/latex] from the left side of the equation, we must also subtract [latex]3[/latex] from the right side to keep the equation balanced.
[latex]x+3\;\;\;\;\;\;=5 \\ x+3\color{blue}{-3}=5\color{blue}{-3} \\ x\;\;\;\;\;\;\;\;\;\;\;\;\,=2[/latex]
We can verify that [latex]x=2[/latex] is indeed the solution by substituting [latex]2[/latex] in for [latex]x[/latex] in the original equation: [latex]x+3=5 \\ 2+3=5 \\ 5=5[/latex] Since this is true, [latex]x=2[/latex] is the solution of [latex]x+3=5[/latex].
If the equation is [latex]x-5=9[/latex], we isolate the variable by adding [latex]5[/latex] to both sides of the equation. This is because, to isolate [latex]x[/latex] we must “undo” subtract [latex]5[/latex] by adding [latex]5[/latex]:
[latex]x-5=9 \\ x-5\color{blue}{+5}=9\color{blue}{+5} \\ x\;\;\;\;\;\;\;\;\;\;\;\;\,=14[/latex]
Again, we can verify the solution: [latex]x-5\;\;\;\;\;\;=9 \\ 14 - 5 = 9 \\ 9=9[/latex] True.
When we add or subtract the same term to both sides of an equation, we get an equivalent equation. Equivalent equations are two or more equations that have identical solutions. This leads us to the the Addition and Subtraction Property of Equality.
Addition & subtraction Property of Equality
For all real numbers [latex]a,b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a+c=b+c[/latex] and [latex]a-c=b-c[/latex].
Adding or subtracting the same term to both sides of an equation will result in an equivalent equation.
EXAMPLE
Solve: [latex]x+11=-3[/latex]
Solution:
To isolate [latex]x[/latex], we undo the addition of [latex]11[/latex] by using the Subtraction Property of Equality.
| [latex]x+11=-3[/latex] | ||
| Subtract 11 from each side to “undo” the addition. | [latex]x+11\color{red}{-11}=-3\color{red}{-11}[/latex] | |
| Simplify. | [latex]x=-14[/latex] | |
| Check: | [latex]x+11=-3[/latex] | |
| Substitute [latex]x=-14[/latex] . | [latex]\color{red}{-14}+11\stackrel{\text{?}}{=}-3[/latex] | |
| [latex]-3=-3\quad\checkmark[/latex] | ||
Since [latex]x=-14[/latex] makes [latex]x+11=-3[/latex] a true statement, we know that it is a solution to the equation.
TRY IT
EXAMPLE
Solve: [latex]m - 4=-5[/latex]
Solution:
| [latex]m-4=-5[/latex] | ||
| Add 4 to each side to “undo” the subtraction. | [latex]m-4\color{red}{+4}=-5\color{red}{+4}[/latex] | |
| Simplify. | [latex]m=-1[/latex] | |
| Check: | [latex]m-4=-5[/latex] | |
| Substitute [latex]m=-1[/latex] . | [latex]\color{red}{-1}+4\stackrel{\text{?}}{=}-5[/latex] | |
| [latex]-5=-5\quad\checkmark[/latex] | ||
| The solution to [latex]m - 4=-5[/latex] is [latex]m=-1[/latex] | ||
TRY IT
Linear Equations Containing Fractions
It is not uncommon to encounter equations that contain fractions; therefore, in the following examples, we will demonstrate how to use the addition property of equality to solve an equation with fractions.
EXAMPLE
Solve: [latex]n-\frac{3}{8} =\frac{1}{2}[/latex]
Solution
| [latex]n-\frac{3}{8} =\frac{1}{2}[/latex] | ||
| Use the Addition Property of Equality. | [latex]n-\frac{3}{8}\color{red}{+\frac{3}{8}} =\frac{1}{2}\color{red}{+\frac{3}{8}}[/latex] | |
| Find the LCD to add the fractions on the right. | [latex]n\frac{3}{8} +\frac{3}{8} =\frac{4}{8} +\frac{3}{8}[/latex] | |
| Simplify. | [latex]n=\frac{7}{8}[/latex] | |
| Check: | [latex]n-\frac{3}{8} =\frac{1}{2}[/latex] | |
| Substitute [latex]n=\color{red}{\frac{7}{8}}[/latex] | [latex]\color{red}{\frac{7}{8}} -\frac{3}{8}\stackrel{\text{?}}{=}\frac{1}{2}[/latex] | |
| Subtract. | [latex]\frac{4}{8}\stackrel{\text{?}}{=}\frac{1}{2}[/latex] | |
| Simplify. | [latex]\frac{1}{2}\normalsize =\frac{1}{2}\normalsize\quad\checkmark[/latex] | |
| The solution checks. | ||
TRY IT
Watch this video for more examples of solving equations that include fractions and require addition or subtraction.
Linear Equations Containing Decimals
Decimals will be encountered any time money or metric measurements are used.
eXAMPLE
Solve [latex]a - 3.7=4.3[/latex]
Solution
| [latex]a-3.7=4.3[/latex] | ||
| Use the Addition Property of Equality. | [latex]a-3.7\color{red}{+3.7}=4.3\color{red}{+3.7}[/latex] | |
| Add. | [latex]a=8[/latex] | |
| Check: | [latex]a-3.7=4.3[/latex] | |
| Substitute [latex]a=8[/latex] . | [latex]\color{red}{8}-3.7\stackrel{\text{?}}{=}4.3[/latex] | |
| Simplify. | [latex]4.3=4.3\quad\checkmark[/latex] | |
| The solution checks. | ||
TRY IT
The Multiplication and Division Properties of Equality
Just as we can add or subtract the same exact quantity on both sides of an equation, we can also multiply or divide both sides of an equation by the same quantity to write an equivalent equation. This makes sense because multiplication is just repeated addition and division is multiplication by a reciprocal.
For example, to solve the equation [latex]3x=15[/latex] we need to isolate the variable [latex]x[/latex] which is multiplied by [latex]3[/latex]. To “undo” this multiplication, we divide both sides of the equation by [latex]3[/latex]: [latex]\frac{3x}\color{blue}{{3}}=\frac{15}\color{blue}{{3}}[/latex]. Since [latex]\frac{3}{3}=1[/latex] and [latex]1x=x[/latex], this simplifies to [latex]x=5[/latex] and we have our solution.
On the other hand, in the equation [latex]\frac{1}{2}x=-5[/latex] the variable [latex]x[/latex] is multiplied by [latex]\frac{1}{2}[/latex]. To isolate the variable we need to turn [latex]\frac{1}{2}[/latex] into [latex]1[/latex] by multiplying by the reciprocal [latex]2[/latex]: [latex]\color{blue}{2}\left(\frac{1}{2}x\right)=\color{blue}{2}(-5)[/latex]. This simplifies to [latex]x=-10[/latex] and we have our solution.
This characteristic of equations is generalized in the Multiplication & Division Property of Equality.
multiplication & Division Property of Equality
For all real numbers [latex]a,b,c[/latex], and [latex]c\ne 0[/latex], if [latex]a=b[/latex], then [latex]ac=bc[/latex] and [latex]\Large\frac{a}{c}\normalsize =\Large\frac{b}{c}[/latex].
Multiplying or dividing the same non-zero* term to both sides of an equation will result in an equivalent equation.
*Technically we could multiply both sides of an equation by zero but that would wipe out our entire equation to [latex]0=0[/latex]. However, we can never divide by zero as that is undefined.
When the equation involves multiplication or division, we can “undo” these operations by using the inverse operation to isolate the variable.
Example
Solve [latex]3x=24[/latex]. When you are done, check your solution.
Solution
Divide both sides of the equation by [latex]3[/latex] to isolate the variable (this is will give you a coefficient of [latex]1[/latex]). Dividing by [latex]3[/latex] is the same as multiplying by [latex]\frac{1}{3}[/latex].
[latex]\begin{array}{r}\underline{3x}=\underline{24}\\3\,\,\,\,\,\,\,\,\,\,\,\,3\,\\x=8\,\,\,\end{array}[/latex]
Check by substituting your solution, [latex]8[/latex], for the variable in the original equation.
[latex]\begin{array}{r}3x=24 \\ 3\cdot8=24 \\ 24=24\end{array}[/latex]
The solution is correct!
Answer
[latex]x=8[/latex]
example
Solve: [latex]\frac{a}{-7} =-42[/latex]
Solution
Here [latex]a[/latex] is divided by [latex]-7[/latex]. We can multiply both sides by [latex]-7[/latex] to isolate [latex]a[/latex].
| [latex]\Large\frac{a}{-7}\normalsize =-42[/latex] | |
| Multiply both sides by [latex]-7[/latex] . | [latex]\color{red}{-7}(\frac{a}{-7})=\color{red}{-7}(-42)[/latex]
[latex] \frac{-7a}{-7}=294[/latex] |
| Simplify. | [latex]a=294[/latex] |
| Check your answer. | [latex]\frac{a}{-7}=-42[/latex] |
| Let [latex]a=294[/latex] . | [latex]\frac{\color{red}{294}}{-7}\stackrel{\text{?}}{=}-42[/latex] |
| [latex]-42=-42\quad\checkmark[/latex] |
try it
Another way to think about solving an equation when the operation is multiplication or division is that we want to multiply the coefficient by the multiplicative inverse (reciprocal) in order to change the coefficient to [latex]1[/latex].
In the following example, we change the coefficient to [latex]1[/latex] by multiplying by the multiplicative inverse of [latex]\frac{1}{2}[/latex].
Example
Solve [latex]\frac{1}{2}x=8[/latex] for [latex]x[/latex].
Solution
We can multiply both sides by the reciprocal of [latex]\frac{1}{2}[/latex], which is [latex]\frac{2}{1}[/latex].
[latex]\begin{array}{r}\color{blue}{\left(\frac{2}{1}\right)}\frac{1}{2 }{ x }=\color{blue}{\left(\frac{2}{1}\right)}8\\(1)x= 16\,\,\,\,\\{ x }=16\,\,\,\,\,\end{array}[/latex]
The video shows examples of how to use the Multiplication and Division Property of Equality to solve one-step equations with integers and fractions.
example
Solve: [latex]4x=-28[/latex]
Solution:
To solve this equation, we use the Division Property of Equality to divide both sides by [latex]4[/latex].
| [latex]4x=-28[/latex] | |
| Divide both sides by 4 to undo the multiplication. | [latex]\Large\frac{4x}{\color{red}4}\normalsize =\Large\frac{-28}{\color{red}4}[/latex] |
| Simplify. | [latex]x =-7[/latex] |
| Check your answer. | [latex]4x=-28[/latex] |
| Let [latex]x=-7[/latex]. Substitute [latex]-7[/latex] for x. | [latex]4(\color{red}{-7})\stackrel{\text{?}}{=}-28[/latex] |
| [latex]-28=-28[/latex] |
Since this is a true statement, [latex]x=-7[/latex] is a solution to [latex]4x=-28[/latex].
try it
As we solve equations that require several steps, it is not unusual to end up with an equation that looks like the one in the next example, with a negative sign in front of the variable.
example
Solve: [latex]-r=2[/latex]
Solution:
Remember [latex]-r[/latex] is equivalent to [latex]-1r[/latex].
| [latex]-r=2[/latex] | |
| Rewrite [latex]-r[/latex] as [latex]-1r[/latex] . | [latex]-1r=2[/latex] |
| Divide both sides by [latex]-1[/latex] . | [latex]\Large\frac{-1r}{\color{red}{-1}}\normalsize =\Large\frac{2}{\color{red}{-1}}[/latex] |
| Simplify. | [latex]r=-2[/latex] |
| Check. | [latex]-r=2[/latex] |
| Substitute [latex]r=-2[/latex] | [latex]-(\color{red}{-2})\stackrel{\text{?}}{=}2[/latex] |
| Simplify. | [latex]2=2\quad\checkmark[/latex] |
try it
The equations [latex]x=4[/latex] and [latex]4=x[/latex] are equivalent. Both say that [latex]x[/latex] is equal to [latex]4[/latex]. This is an example of The Reflection Property of Equality.
The Reflection Property of Equality
If [latex]a=b[/latex], then [latex]b=a[/latex], for all real numbers [latex]a[/latex] and [latex]b[/latex].
This implies that it does not matter which side of the equation the variable term ends up on.
The next video includes examples of using the division and multiplication properties to solve equations with the variable on the right side of the equal sign.
Two-Step Linear Equations
If the equation is in the form [latex]ax+b=c[/latex], where [latex]x[/latex] is the variable, we can solve the equation as before. First we must isolate the [latex]x-[/latex]term by “undoing” the addition or subtraction. Then we isolate the variable by “undoing” the multiplication or division.
Example
1. Solve: [latex]4x+6=-14[/latex]
Solution:
In this equation, the variable is only on the left side. It makes sense to call the left side the variable side. Therefore, the right side will be the constant side.
| Since the left side is the variable side, the 6 is out of place. We must “undo” adding [latex]6[/latex] by subtracting [latex]6[/latex], and to keep the equality we must subtract [latex]6[/latex] from both sides. Use the Subtraction Property of Equality. | [latex]4x+6\color{red}{-6}=-14\color{red}{-6}[/latex] | |
| Simplify. | [latex]4x=-20[/latex] | |
| Now all the [latex]x[/latex] s are on the left and the constant on the right. | ||
| Use the Division Property of Equality. | [latex]\Large\frac{4x}{\color{red}{4}}\normalsize =\Large\frac{-20}{\color{red}{4}}[/latex] | |
| Simplify. | [latex]x=-5[/latex] | |
| Check: | [latex]4x+6=-14[/latex] | |
| Let [latex]x=-5[/latex] . | [latex]4(\color{red}{-5})+6=-14[/latex] | |
| [latex]-20+6=-14[/latex] | ||
| [latex]-14=-14\quad\checkmark[/latex] | ||
2. Solve: [latex]2y - 7=15[/latex]
Solution:
Notice that the variable is only on the left side of the equation, so this will be the variable side, and the right side will be the constant side. Since the left side is the variable side, the [latex]7[/latex] is out of place. It is subtracted from the [latex]2y[/latex], so to “undo” subtraction, add [latex]7[/latex] to both sides.
| [latex]2y-7[/latex] is the side containing a variable.[latex]15[/latex] is the side containing only a constant. | ||
| Add [latex]7[/latex] to both sides. | [latex]2y-7\color{red}{+7}=15\color{red}{+7}[/latex] | |
| Simplify. | [latex]2y=22[/latex] | |
| The variables are now on one side and the constants on the other. | ||
| Divide both sides by [latex]2[/latex]. | [latex]\Large\frac{2y}{\color{red}{2}}\normalsize =\Large\frac{22}{\color{red}{2}}[/latex] | |
| Simplify. | [latex]y=11[/latex] | |
| Check: | [latex]2y-7=15[/latex] | |
| Let [latex]y=11[/latex] . | [latex]2\cdot\color{red}{11}-7\stackrel{\text{?}}{=}15[/latex] | |
| [latex]22-7\stackrel{\text{?}}{=}15[/latex] | ||
| [latex]15=15\quad\checkmark[/latex] | ||
Example
Solve [latex]3y+2=11[/latex]
Solution
Subtract [latex]2[/latex] from both sides of the equation to get the term with the variable by itself.
[latex]\displaystyle \begin{array}{r}3y+2\,\,\,=\,\,11\\\underline{\,\,\,\,\,\,\,\color{blue}{-2}\,\,\,\,\,\,\,\,\color{blue}{-2}}\\3y\,\,\,\,=\,\,\,\,\,9\end{array}[/latex]
Divide both sides of the equation by [latex]3[/latex] to get a coefficient of [latex]1[/latex] for the variable.
[latex]\begin{array}{r}\,\,\,\,\,\,\underline{3y}\,\,\,\,=\,\,\,\,\,\underline{9}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9\\\,\,\,\,\,\,\,\,\,\,y\,\,\,\,=\,\,\,\,3\end{array}[/latex]
Answer
[latex]y=3[/latex]
Try It
In the following video, we show examples of solving two step linear equations.
Remember to check the solution of an algebraic equation by substituting the value of the variable into the original equation.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. . Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Linear Equations with No Solutions of Infinite Solutions.. Authored by: James Sousa . Provided by: (Mathispower4u.com) for Lumen Learning.. Located at: https://youtu.be/EU_NEo1QBJ0.. License: CC BY: Attribution
- Definition of a Linear Equation. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Beginning and Intermediate Algebra.. Authored by: Tyler Wallace.. Located at: http://wallace.ccfaculty.org/book/book.html.. License: CC BY: Attribution
- Unit 10: Solving Equations and Inequalities, from Developmental Math: An Open Program. . Provided by: Monterey Institute of Technology and Education.. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/.. License: CC BY: Attribution
