Learning Objectives
- Solve a system of linear equation using the elimination method
The Elimination Method
In the last section, we solved systems of linear equations using the elimination method. In this method, we add equations where one of the variables has opposite coefficients in the equations, so that the sum is zero. This eliminates that variable and results in a linear equation in one variable which can be solved, a contradiction that implies no solution, or an identity which implies infinite solutions constrained by either equation. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.
the ELIMINATION method
- Write both equations with [latex]x[/latex]– and [latex]y[/latex]-variables on the left side of the equals sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by nonzero numbers so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable. If a contradiction occurs, there is no solution. If an identity occurs, there are infinite solutions constrained by either equation.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Example
Solve the system of equations:
[latex]\begin{align}x+2y&=-1 \\ -x+\;y&=3 \end{align}[/latex]
Solution
Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, –1, is the opposite of the coefficient of [latex]x[/latex] in the first equation, 1. We can add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant:
[latex]\begin{align} x+2y&=-1 \\ -x+y&=3 \\ \hline 0x+3y&=2\end{align}[/latex]
Now that we have eliminated [latex]x[/latex], we can solve the resulting equation for [latex]y[/latex]:
[latex]\begin{align}3y&=2 \\ y&=\dfrac{2}{3} \end{align}[/latex]
Now substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex]:
[latex]\begin{align}-x+y&=3 \\ -x+\frac{2}{3}&=3 \\ -x&=3-\frac{2}{3} \\ -x&=\frac{7}{3} \\ x&=-\frac{7}{3} \end{align}[/latex]
The solution to this system is [latex]\left(-\frac{7}{3},\frac{2}{3}\right)[/latex].
Check the solution in the other equation:
[latex]\begin{align}x+2y&=-1 \\ \left(-\frac{7}{3}\right)+2\left(\frac{2}{3}\right)&= \\ -\frac{7}{3}+\frac{4}{3}&= \\ -\frac{3}{3}&= \\ -1&=-1&& \text{True} \end{align}[/latex]
Solution
The solution is [latex]\left(-\frac{7}{3},\frac{2}{3}\right)[/latex].
Analysis of the Solution
We gain an important perspective on systems of equations by looking at the graphical representation. See the graph below to find that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.
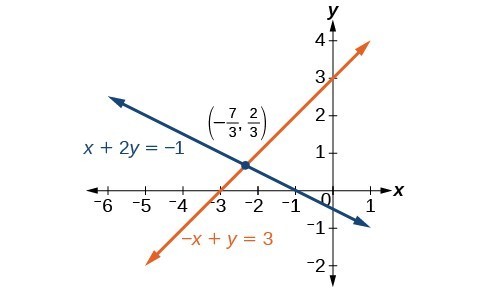
Try It
Example
Solve the given system of equations:
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Solution
Adding these equations as presented will not eliminate a variable. However, the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the [latex]x[/latex]-terms will add to zero:
[latex]\begin{align}x - 2y&=11 \\\color{red}{-3}\left(x - 2y\right)&=\color{red}{-3}\left(11\right) && \text{Multiply both sides by }-3 \\ -3x+6y&=-33 && \text{Use the distributive property}. \end{align}[/latex]
Now, let’s add them:
[latex]\begin{align}3x+5y&=−11 \\ −3x+6y&=−33 \\ \hline 0x+11y&=−44 \\ y&=−4 \end{align}[/latex]
Next, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex]:
[latex]\begin{align}3x+5y&=-11\\ 3x+5\left(-4\right)&=-11\\ 3x - 20&=-11\\ 3x&=9\\ x&=3\end{align}[/latex]
Our solution is [latex]\left(3,-4\right)[/latex]. Check the solution in the other original equation:
[latex]\begin{align}x - 2y&=11 \\ \left(3\right)-2\left(-4\right)&=3+8 \\ &=11 && \text{True} \end{align}[/latex]
Answer
The solution is [latex]\left(3,-4\right)[/latex].
Analysis of the solution
Graphically, the two lines represented by the equations cross at the single point [latex]\left(3,-4\right)[/latex].
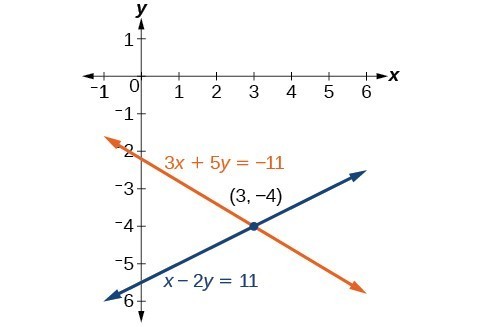
Notice that we go back to the original equations to check our solution. This will catch any arithmetical error we may have made when multiplying or adding the equations, as well as guaranteeing that our answer is the actual solution of the system.
Try It
Try It
Solve the system of equations:
[latex]\begin{equation}\begin{aligned}5x+4y&=12\\3x-2y&=-6\end{aligned}\end{equation}[/latex]
Sometimes, it is not enough to multiply just one of the equations by a non-zero number to attain opposite coefficients of a variable. The next example shows how to get opposite coefficients of a variable by multiplying both equations.
Example
Solve the given system of equations in two variables by addition.
[latex]\begin{align}2x+3y&=-16 \\ 5x - 10y&=30\end{align}[/latex]
Solution
One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. Both of the coefficients divide exactly into 10, so we can multiply the equations by [latex]5[/latex] and [latex]2[/latex], respectively, to get equal coefficients of [latex]10[/latex]. However, to eliminate [latex]x[/latex] one of the coefficients must be [latex]-10[/latex], so we will multiply the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex]:
[latex]\begin{align} \color{red}{-5}\left(2x+3y\right)&=\color{red}{-5}\left(-16\right) \\ -10x - 15y&=80 \\[3mm]\color{red}{2}\left(5x - 10y\right)&=\color{red}{2}\left(30\right) \\ 10x - 20y&=60 \end{align}[/latex]
Then, we add the two equations together to eliminate [latex]x[/latex]:
[latex]\begin{align} −10x−15y&=80 \\ 10x−20y&=60 \\ \hline 0x−35y&=140 \\ y&=−4 \end{align}[/latex]
Substitute [latex]y=-4[/latex] into the original first equation:
[latex]\begin{align}2x+3\left(-4\right)&=-16\\ 2x - 12&=-16\\ 2x&=-4\\ x&=-2\end{align}[/latex]
The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the other equation:
[latex]\begin{align} 5x - 10y&=30\\ 5\left(-2\right)-10\left(-4\right)&=30\\ -10+40&=30\\ 30&=30\;\;\;\text{True}\end{align}[/latex]
Answer
The solution is [latex]\left(-2,-4\right)[/latex].
Analysis
Graphically, the two lines represented by the equations cross at a single point [latex]\left(-2,-4\right)[/latex].
It is possible for a system of equations contains fractions. Fortunately, we can write equivalent equations that do not contain fractions by multiplying by a common denominator.
Example
Solve the given system of equations in two variables by addition.
[latex]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1mm] \frac{x}{2}-\frac{y}{4}&=1 \end{align}[/latex]
Solution
First clear each equation of fractions by multiplying both sides of the equation by the least common denominator. The LCD for the first equation is [latex]6[/latex] so we multiply the entire equation by [latex][/latex]:
[latex]\begin{align}\color{red}{6}\left(\frac{x}{3}+\frac{y}{6}\right)&=\color{red}{6}\left(3\right) \\[1mm] 2x+y&=18 \end{align}[/latex]
The LCD for the second equation is [latex]4[/latex] so we multiply the entire equation by [latex]4[/latex]:
[latex]\begin{align}2x+y&=18 \\[3mm]\color{red}{4}\left(\frac{x}{2}-\frac{y}{4}\right)&=\color{red}{4}\left(1\right) \\[1mm] 2x-y&=4 \end{align}[/latex]
Now multiply the second equation by [latex]-1[/latex] so that we can eliminate [latex]x[/latex]:
[latex]\begin{align}-1\left(2x-y\right)&=-1\left(4\right) \\[1mm] -2x+y&=-4 \end{align}[/latex]
Add the two equations to eliminate [latex]x[/latex] and solve the resulting equation for [latex]y[/latex]:
[latex]\begin{align} 2x+y&=18 \\ −2x+y&=−4 \\ \hline 2y&=14 \\ y&=7 \end{align}[/latex]
Substitute [latex]y=7[/latex] into the first equation and solve for [latex]x[/latex]:
[latex]\begin{align}2x+\left(7\right)&=18 \\ 2x&=11 \\ x&=\frac{11}{2} \\ &=7.5 \end{align}[/latex]
The solution is [latex]\left(\frac{11}{2},7\right)[/latex]. Check it in the other equation:
[latex]\begin{align}\frac{x}{2}-\frac{y}{4}&=1\\[1mm] \frac{\frac{11}{2}}{2}-\frac{7}{4}&=1\\[1mm] \frac{11}{4}-\frac{7}{4}&=1\\[1mm] \frac{4}{4}&=1\end{align}[/latex]
Answer
The solution is [latex]\left(\frac{11}{2},7\right)[/latex].
TRY IT
TRY IT
Solve the system of equations:
[latex]\begin{equation}\begin{aligned}\frac{3}{4}x-y=2\\3x-4y=8\end{aligned}\end{equation}[/latex]
The following video presents more examples of how to use the elimination method to solve a system of two linear equations.
