Learning Outcomes
- Define a polynomial
- Determine the degree of a polynomial
- Classify a polynomial as a monomial, binomial or trinomial
- Determine the leading term and leading coefficient of a polynomial
- Write a polynomial in standard form (descending order)
Key WORDS
- Term: a number, variable, or product or quotient of numbers and variables
- Coefficient: a number multiplied onto a variable; the number in a term
- Algebraic expression: terms that are combined using operations like [latex]+,\;-,\;\times,\;\div[/latex]. etc.
- Polynomial: an algebraic expression of the form [latex]a_{n}x^n+a_{n-1}x^{n-1}+ ... + a_{1}x+a_{0}[/latex]
- Monomial:a polynomial with one terms
- Binomial: a polynomial with two terms
- Trinomial: a polynomial with three terms
- Degree: the largest exponent
- Descending order: written from highest to lowest terms based on degree
- Standard Form: a polynomial written in descending order
- Leading term: the monomial with the highest degree
- Leading coefficient: the coefficient of the leading term
Polynomials in One Variable
We previously defined a term to be a number, a variable, or the product or quotient of numbers and variables. For example, [latex]6x,\; \frac{4x^2}{5y^3},\; -4x^3y^2[/latex] are all terms. The coefficient of a term is the number in the term. So, for the list of examples just given, the coefficients are, [latex]6,\;\frac{4}{5},\;-4[/latex]. When algebraic terms are combined using operations like [latex]+,\;-,\;\times,\;\div[/latex]. etc., they form an algebraic expression. For example, [latex]5x^3-\frac{3}{4x^2}+6[/latex] is an algebraic expression containing three terms.
A polynomial in one variable is a special algebraic expression that consists of a term or a sum (or difference) of terms in which each term is a real number, a variable, or the product of a real number and a variable with a whole number exponent.
For example,
[latex]5x^2+7x-3[/latex] is a polynomial with three terms: [latex]5x^2,\;7x,\;-3[/latex]. The coefficient of [latex]x^2[/latex] is [latex]5[/latex]; the coefficient of [latex]x[/latex] is [latex]7[/latex]; and [latex]-3[/latex] is the constant term.
[latex]-\frac{4}{3}x^9+8x^4-\frac{3}{5}x^2-9[/latex] is a polynomial with four terms: [latex]-\frac{4}{3}x^9,\;8x^4,\;-\frac{3}{5}x^2,\;-9[/latex]. The coefficient of [latex]x^9[/latex] is [latex]-\frac{4}{3}[/latex]; the coefficient of [latex]x^4[/latex] is [latex]8[/latex]; the coefficient of [latex]x^2[/latex] is [latex]\frac{3}{5}[/latex]; the constant term [latex]-9[/latex].
[latex]\sqrt{5}x^3[/latex] and [latex]4.563[/latex] are polynomials with just one term.
However, [latex]\frac{3}{x},\;\;x^{\frac{1}{2}},\;\;\frac{4}{y^2}-4x^3[/latex] are NOT polynomials because the exponents on the variables are not whole numbers. Whole number exponents exclude radicals (fractional exponents) and variables on the denominator of a fraction (negative exponents).
The following table is intended to help us tell the difference between what is a polynomial and what is not.
| IS a Polynomial | Is NOT a Polynomial | Because |
| [latex]2x^2-\frac{1}{2}x -9[/latex] | [latex]\frac{2}{x^{2}}+x[/latex] | Polynomials only have variables in the numerator |
| [latex]\frac{y}{4}-y^3[/latex] | [latex]\frac{2}{y}+4[/latex] | Polynomials only have variables in the numerator |
| [latex]\sqrt{12}\left(a\right)+9[/latex] | [latex]\sqrt{a}+7[/latex] | Variables under a root are not allowed in polynomials |
The basic building block of a polynomial is a monomial. A monomial is a term of the form [latex]a{x}^{n}[/latex], where [latex]a[/latex] is a constant and [latex]n[/latex] is a whole number. A monomial can be a number, a variable, or the product of a number and variable with an exponent. The number part of the term is called the coefficient.
Examples of monomials:
- constant: [latex]{6}[/latex]
- variable with a coefficient of [latex]1[/latex]: [latex]{x}[/latex]
- product of a coefficient and a variable: [latex]{6x}[/latex]
- product of a coefficient and a variable with a whole number exponent: [latex]6{x}^{3}[/latex]

The coefficient can be any real number, including [latex]0[/latex]. The exponent of the variable must be a whole number (i.e., [latex]0, 1, 2, 3,...[/latex]). The value of the exponent is the degree of the monomial. Remember that a variable, such as [latex]x[/latex], that appears to have no exponent really has an exponent of [latex]1[/latex]: [latex]x=x^1[/latex]. A monomial with no variable has a degree of [latex]0[/latex]. A number such as [latex]3[/latex] can be written as [latex]3x^{0}[/latex], since [latex]x^{0}=1[/latex] if [latex]x\neq0[/latex]. A monomial cannot have a variable in the denominator as that would have a negative exponent, nor can it have a variable under a radical as that would have a fractional exponent.
Example
Identify the coefficient, variable, and degree of the monomial:
1) [latex]9[/latex]
2) [latex]x[/latex]
3) [latex]\displaystyle \frac{3}{5}{{k}^{8}}[/latex]
Solution
1) [latex]9[/latex] is a constant so there is no variable. Since [latex]9=9x^0[/latex], the degree is [latex]0[/latex] and the coefficient is [latex]9[/latex]. [latex]9[/latex] is called a constant term.
2) The variable is [latex]x[/latex].
The degree of [latex]x[/latex] is [latex]1[/latex], because [latex]x=x^{1}[/latex].
The coefficient of [latex]x[/latex] is [latex]1[/latex], because [latex]x=1x[/latex].
3) The variable is [latex]k[/latex].
The degree of[latex]\displaystyle \frac{3}{5}{{k}^{8}}[/latex] is [latex]8[/latex].
The coefficient of [latex]k^{8}[/latex] is [latex]\displaystyle \frac{3}{5}[/latex].
Try It
Identify the coefficient, variable, and degree of the monomial:
1. [latex]6x^7[/latex]
2. [latex]-9x[/latex]
3. [latex]\frac{4}{7}[/latex]
Classifying Polynomials
The word polynomial joins two diverse roots: the Greek poly, meaning “many”, and the Latin nomen, meaning “name.” Consequently, polynomial means many names, or in math, many terms. In this section, we will look at different ways that we classify polynomials. First, we will classify polynomials by the number of terms in the polynomial and then we will classify them by the largest exponent.
By Number of Terms
A polynomial is defined as a monomial or the sum (or difference) of monomials. This means that a polynomial that contains just one term is called a monomial. A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. After three terms we tend to simply refer to them as polynomials.
Polynomials
polynomial—A monomial; or two or more monomials, combined by addition (or subtraction)
monomial—A polynomial with exactly one term (“mono” means one)
binomial— A polynomial with exactly two terms (“bi” means two)
trinomial—A polynomial with exactly three terms (“tri” means three)
Here are some examples of polynomials classified by the number of terms.
| Polynomial | [latex]b+1[/latex] | [latex]4{y}^{2}-7y+2[/latex] | [latex]5{x}^{5}-4{x}^{4}+{x}^{3}+8{x}^{2}-9x+1[/latex] |
| Monomial | [latex]5[/latex] | [latex]4{b}^{2}[/latex] | [latex]-9{x}^{3}[/latex] |
| Binomial | [latex]3a - 7[/latex] | [latex]{y}^{2}-9[/latex] | [latex]17{x}^{3}+14{x}^{2}[/latex] |
| Trinomial | [latex]{x}^{2}-5x+6[/latex] | [latex]4{y}^{2}-7y+2[/latex] | [latex]5{a}^{4}-3{a}^{3}+a[/latex] |
Notice that every monomial, binomial, and trinomial is also a polynomial. in other words:
{monomials} [latex]\subset[/latex] {binomials} [latex]\subset[/latex] {trinomials} [latex]\subset[/latex] {polynomials}
example
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial:
1. [latex]8{x}^{2}-7x - 9[/latex]
2. [latex]-5{a}^{4}[/latex]
3. [latex]{x}^{4}-7{x}^{3}-6{x}^{2}+5x+2[/latex]
4. [latex]11 - 4{y}^{3}[/latex]
5. [latex]n[/latex]
Solution
| Polynomial | Number of terms | Type | |
|---|---|---|---|
| 1. | [latex]8{x}^{2}-7x - 9[/latex] | [latex]3[/latex] | Trinomial |
| 2. | [latex]-5{a}^{4}[/latex] | [latex]1[/latex] | Monomial |
| 3. | [latex]{x}^{4}-7{x}^{3}-6{x}^{2}+5x+2[/latex] | [latex]5[/latex] | Polynomial |
| 4. | [latex]11 - 4{y}^{3}[/latex] | [latex]2[/latex] | Binomial |
| 5. | [latex]n[/latex] | [latex]1[/latex] | Monomial |
Example
For the following expressions, determine whether they are a polynomial. If so, categorize them as a monomial, binomial, or trinomial.
- [latex]\frac{x-3}{1-x}+x^2[/latex]
- [latex]t^2+2t-3[/latex]
- [latex]x^3+\frac{x}{8}[/latex]
- [latex]\frac{\sqrt{y}}{2}-y-1[/latex]
Solution
- [latex]\frac{x-3}{1-x}+x^2[/latex] is not a polynomial because it violates the rule that polynomials cannot have variables in the denominator of a fraction (negative exponent).
- [latex]t^2+2t-3[/latex] is a polynomial because it is an expression whose monomial terms are connected by addition and subtraction. There are three terms in this polynomial so it is a trinomial.
- [latex]x^3+\frac{x}{8}[/latex]is a polynomial because it is an expression whose monomial terms are connected by addition and subtraction. There are two terms in this polynomial so it is a binomial.
- [latex]\frac{\sqrt{y}}{2}-y-1[/latex] is not a polynomial because it violates the rule that polynomials cannot have variables under a root (fractional exponent).
try it
The following video shows more examples of how to identify and categorize polynomials.
By Degree
We can find the degree of a one variable polynomial by identifying the highest power of the variable that occurs in the polynomial. Polynomials can be classified by the degree of the polynomial. The degree of a polynomial is the degree of its highest degree monomial term. So the degree of [latex]2x^{3}+3x^{2}+8x+5[/latex] is [latex]3[/latex].
A one variable polynomial is said to be written in standard form when the terms are arranged from the highest degree to the lowest degree. This is referred to as descending order. When it is written in standard form it is easy to determine the degree of the polynomial. The term with the highest degree is called the leading term because it is written first in standard form. The coefficient of the leading term is called the leading coefficient.
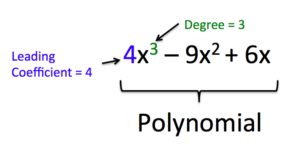
Degree of a ONE VARIABLE Polynomial
The degree of a term is the exponent of its variable.
The degree of a constant is [latex]0[/latex].
The degree of a polynomial is the highest degree of all its terms.
When the coefficient of a polynomial term is [latex]0[/latex], e.g., [latex]0x^2[/latex], we usually do not write the term at all because [latex]0x^n=0[/latex], and adding [latex]0[/latex] does not change the value of the polynomial. However, we will see later, that occasionally, it is necessary to include all terms of the polynomial, including terms with zero coefficients.
A term without a variable is called a constant term, and the degree of that term is [latex]0[/latex]. This is because any constant [latex]a[/latex] can be written as [latex]ax^0[/latex], since [latex]x^0=1[/latex]. For example, we can write the polynomial [latex]3x+13[/latex] as [latex]3x^{1}+13x^{0}[/latex]. Although this is not how we would normally write this, it allows us to see that [latex]13[/latex] is the constant term because its degree is 0, and the degree of [latex]3x[/latex] is 1. Consequently, the degree of the binomial[latex]3x+13[/latex] is 1.
If a polynomial does not have a constant term, like the polynomial [latex]14x^{3}+3x[/latex] we say that the constant term is [latex]0[/latex].
Let’s see how this works by looking at several polynomials. We’ll take it step by step, starting with monomials, and then progressing to polynomials with more terms.
Remember: Any variable base written without an exponent has an implied exponent of [latex]1[/latex], and any constant term has an implied exponent of zero.
| Monomials | [latex]5[/latex] | [latex]4b^2[/latex] | [latex]-9x^3[/latex] | [latex]-18[/latex] |
| Degree | 0 | 2 | 3 | 0 |
| Binomials | [latex]b+\frac{1}{7}[/latex] | [latex]3a-7[/latex] | [latex]y^2-9[/latex] | [latex]17x^3+14x^2[/latex] |
| Degree of each term | 1 0 | 1 0 | 2 0 | 3 2 |
| Degree of polynomial | 1 | 1 | 2 | 3 |
| Trinomial | [latex]x^2-5x+6[/latex] | [latex]4y^2-7y+2[/latex] | [latex]5a^12-3a^9+a[/latex] | [latex]\frac{1}{2}x^4+2x^2-5[/latex] |
| Degree of each term | 2 1 0 | 2 1 0 | 12 9 1 | 4 2 0 |
| Degree of polynomial | 2 | 2 | 12 | 4 |
| Polynomial | [latex]-7x^8+9x^6-7x^4+x^2-8[/latex] | [latex]\frac{3}{5}x^7-8x^6+\frac{7}{8}x+9[/latex] | [latex]5.4x^{17}-8.1x^{13}+2.8x^{10}-6.5x^5[/latex] | [latex]7+6y-9y^2+6y^3-3y^4+y^5[/latex] |
| Degree of each term | 8 6 4 2 0 | 7 6 1 0 | 17 13 10 5 | 0 1 2 3 4 5 |
| Degree of polynomial | 8 | 7 | 17 | 5 |
example
Find the degree of the following polynomials:
1. [latex]4x[/latex]
2. [latex]3{x}^{3}-5x+7[/latex]
3. [latex]-11[/latex]
4. [latex]-6{x}^{2}+9x - 3[/latex]
5. [latex]8x+2[/latex]
Solution
| 1. | [latex]4x[/latex] |
| The exponent of [latex]x[/latex] is one. [latex]x={x}^{1}[/latex] | The degree is [latex]1[/latex]. |
| 2. | [latex]3{x}^{3}-5x+7[/latex] |
| The highest degree of all the terms is [latex]3[/latex]. | The degree is [latex]3[/latex] |
| 3. | [latex]-11[/latex] |
| The degree of a constant is [latex]0[/latex]. | The degree is [latex]0[/latex]. |
| 4. | [latex]-6{x}^{2}+9x - 3[/latex] |
| The highest degree of all the terms is [latex]2[/latex]. | The degree is [latex]2[/latex]. |
| 5. | [latex]8x+2[/latex] |
| The highest degree of all the terms is [latex]1[/latex]. | The degree is [latex]1[/latex]. |
Working with polynomials is easier when we list the terms in descending order of degrees. When a polynomial is written this way, it is said to be in standard form. Look back at the polynomials in the previous example. Notice that they are all written in standard form. Get in the habit of writing polynomials in standard form
try it
Example
For the following polynomials, write them in standard form (descending order), identify the degree, the leading term, and the leading coefficient.
- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}+7t-2{t}^{3}[/latex]
- [latex]6p-{p}^{3}-2[/latex]
Solution
- Standard form: [latex]-4x^32x^2+3[/latex]. The highest power of [latex]x[/latex] is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
- Standard form: [latex]5t^5-2t^3+7t[/latex]. The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
- Standard form:[latex]-p^3+6p-2[/latex]. The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].
The following video shows how to identify the terms, leading coefficient, and degree of a polynomial.
Try It
For the following polynomials, write them in standard form (descending order), identify the degree, the leading term, and the leading coefficient.
- [latex]9+2{x}^{2}-5{x}^{5}[/latex]
- [latex]-5{t}^{5}+7+8t-4{t}^{3}[/latex]
- [latex]4p^4-{p}^{7}-2p[/latex]
Candela Citations
- Determine if an Expression is a Polynomial. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning.. Located at: https://youtu.be/nPAqfuoSbPI. License: CC BY: Attribution
- Revision and Adaption. Authored by: Hazel McKenna and Roxanne Brinkerhoff. Provided by: Utah Valley University. License: CC BY: Attribution
- Ex: Intro to Polynomials in One Variable. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/3u16B2PN9zk. License: CC BY: Attribution
- Try It hjm334; hjm847. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Authored by: Monterey Institute of Technology and Education. License: CC BY: Attribution
