7.1.1 The Rectangular Coordinate System

Learning Outcomes

  • Identify quadrants on the Cartesian plane
  • Identify axes on the Cartesian plane
  • Identify points on the Cartesian plane as ordered pairs
  • Plot ordered pairs as points on a rectangular coordinate system

KEY words

  • Coordinates: an ordered pair written in the form [latex](x,y)[/latex]
  • Origin: the point (0, 0) where the axes cross
  • Perpendicular: sitting at right angles
  • Quadrant: A quarter of the coordinate plane separated by the axes

The Rectangular Coordinate System

The rectangular coordinate system was developed in 1637 and refined by the French mathematician René Descartes. The rectangular coordinate system is often referred to as the Cartesian plane (in honor of Descartes). This system allows us to describe algebraic relationships in a visual sense, and also helps us create and interpret algebraic concepts.

You have likely used a coordinate system before. Many maps use a grid system to identify locations. The map in figure 1 uses a horizontal and vertical grid to convey information about an object’s location. The numbers [latex]1,2,3[/latex], and [latex]4[/latex] across the bottom of the map and the letters A, B, C, and D along the left side identify the columns and rows of the grid, respectively. Every location on the map can be identified by a number and a letter that identifies the cell in the grid.

The general location of any item on this map can be found by using the letter and number of its grid cell. For example, the Student Center is in section 2B. It is located in the grid section above the number [latex]2[/latex] and next to the letter B. The Stadium is in section 4D, and the library is in 2C.

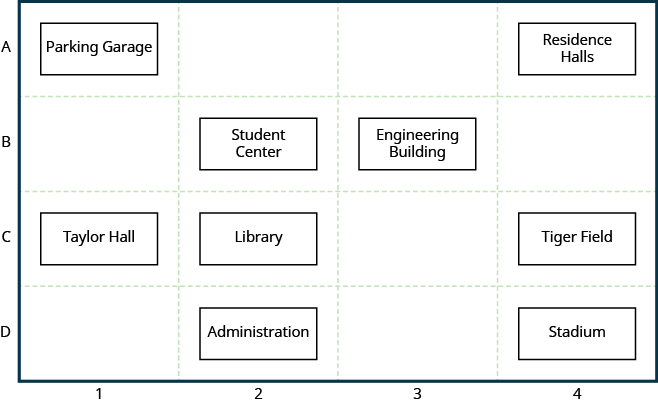
The figure shows a labeled grid representing the Campus Map. The columns are labeled 1 through 4 and the rows are labeled A through D. At position A-1 is the title Parking Garage. At position A-4 is a rectangle labeled Residence Halls. At position B-2 is a rectangle labeled Student Center. At position B-3 is a rectangle labeled Engineering Building. At position C-1 is a rectangle labeled Taylor Hall. At position C-2 is a rectangle labeled Library. At position C-4 is a rectangle labeled Tiger Field. At position D-4 is a rectangle labeled Stadium.

Figure 1. A campus map.

example

Use the map in figure 1.

  1. Find the grid section of the Residence Halls.
  2. What is located in grid section 3B?

Solution

  1. Read the number below the Residence Halls, [latex]4[/latex], and the letter to the side, A. So the Residence Halls are in grid section 4A.
  2. Find [latex]3[/latex] across the bottom of the map and B along the side. Look below the [latex]3[/latex] and next to the B. The engineering building is in grid section 3B.

 

The rectangular coordinate system consists of two basic elements: the rectangular coordinate plane and ordered pairs plotted as points on the plane.  Figure 2 shows the rectangular coordinate plane. It consists of a horizontal axis and a vertical axis. Each axis is a number line and the number lines intersect at right angles forming a two-dimensional plane. The axes are perpendicular to each other and intersect where zero lies on both axes.

The horizontal axis in the coordinate plane is called the [latex]x-axis[/latex]. The vertical axis is called the [latex]y-axis[/latex]. The point at which the two axes intersect is called the origin. The origin is at [latex]0[/latex] on the [latex]x-axis[/latex] and [latex]0[/latex] on the [latex]y-axis[/latex].

The intersecting [latex]x[/latex]– and [latex]y[/latex]–axes of the coordinate plane divide it into four sections. These four sections are called quadrants. Quadrants are named using the Roman numerals I, II, III, and IV beginning with the top right quadrant and moving counter clockwise.

The rectangular coordinate PLANE

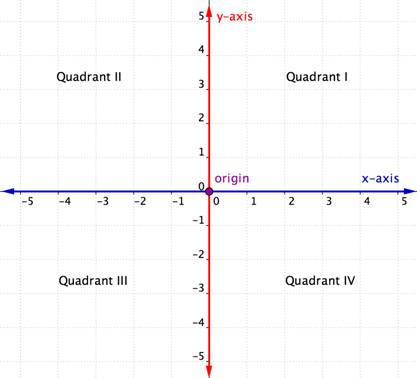
A graph with an x-axis running horizontally and a y-axis running vertically. The location where these axes cross is labeled the origin, and is the point zero, zero. The axes also divide the graph into four equal quadrants. The top right area is quadrant one. The top left area is quadrant two. The bottom left area is quadrant three. The bottom right area is quadrant four.

Figure 2. The rectangular coordinate plane.

Locations on the coordinate plane are described as ordered pairs. An ordered pair tells you the location of a point by relating the point’s location along the [latex]x[/latex]–axis (the first value of the ordered pair) and along the [latex]y[/latex]-axis (the second value of the ordered pair).

In an ordered pair, such as [latex](x, y)[/latex], the first value is called the [latex]x[/latex]–coordinate and the second value is the [latex]y[/latex]-coordinate. Note that the [latex]x[/latex]–coordinate is listed before the [latex]y[/latex]–coordinate. Since the origin has an [latex]x[/latex]–coordinate of [latex]0[/latex] and a [latex]y[/latex]–coordinate of [latex]0[/latex], its ordered pair is written [latex](0, 0)[/latex].

Ordered Pair

An ordered pair, [latex]\left(x,y\right)[/latex] gives the coordinates of a point in a rectangular coordinate system.

[latex]\begin{array}{c}\text{The first number is the }x\text{-coordinate}.\hfill \\ \text{The second number is the }y\text{-coordinate}.\hfill \end{array}[/latex]

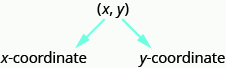
The ordered pair x y is labeled with the first coordinate x labeled as

Plotting Points

Points can be plotted on the rectangular coordinate plane by first locating the [latex]x[/latex] value then locating the [latex]y[/latex] value.

For example, to plot the point [latex]\left(2,5\right)[/latex], first locate [latex]2[/latex] on the [latex]x[/latex]-axis then move vertically to the level of [latex]5[/latex] on the [latex]y[/latex]-axis. We plot the point directly above [latex]2[/latex] on the  [latex]x[/latex]-axis and at the level of [latex]5[/latex] on the [latex]y[/latex]-axis, as shown in figure 3.

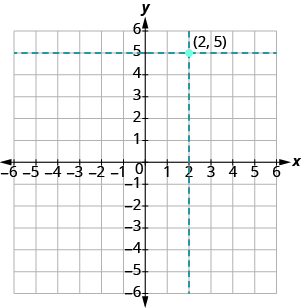
The graph shows the x y-coordinate plane. The x and y-axis each run from -6 to 6. An arrow starts at the origin and extends right to the number 2 on the x-axis. An arrow starts at the end of the first arrow at 2 on the x-axis and goes vertically 5 units to a point labeled

Figure 3. Plotting the point (2, 5).

 

example

Plot [latex]\left(1,3\right)[/latex] and [latex]\left(3,1\right)[/latex] in the same rectangular coordinate system.

try it

 

When one (or both) of the coordinates of an ordered pair is negative, we move in the negative direction along one or both axes.

Example

Plot the point [latex](−4,−2)[/latex].

Graph with blue arrow pointing from origin to four units to the left. A red arrow points down 2 spaces to the point negative 4, negative 2.

The [latex]x-[/latex]coordinate is [latex]−4[/latex] because it comes first in the ordered pair. Start at the origin and move [latex]4[/latex] units in a negative direction (left) along the x-axis.

The [latex]y-[/latex]coordinate is [latex]−2[/latex] because it comes second in the ordered pair. Now move [latex]2[/latex] units in a negative direction (down). If you look over to the y-axis, you should be lined up with [latex]−2[/latex] on that axis.

Now draw a point at that location and label it.

NOTE: A point on the coordinate plane represents a single location. The point has no dimension (no length nor width); although it is physically impossible to draw a dot without dimension.

example

How do the signs affect the location of the points?

Plot each point:

1. [latex]\left(-5,2\right)[/latex]
2. [latex]\left(-5,-2\right)[/latex]
3. [latex]\left(5,2\right)[/latex]
4. [latex]\left(5,-2\right)[/latex]

As we locate the [latex]x\text{-coordinate}[/latex] and the [latex]y\text{-coordinate}[/latex], we must be careful with the signs.

The graph shows the x y-coordinate plane. The x and y-axis each run from -7 to 7. The point

try it

 

Watch the video below for more examples of how to plot ordered pairs.

Identify quadrants and use them to plot points

When we described the rectangular coordinate plane, we mentioned the four quadrants, I, II, III, and IV.  These quadrants can be useful for locating points because ordered pairs within any particular quadrant share certain characteristics. Consider the points in each quadrant in figure 4.

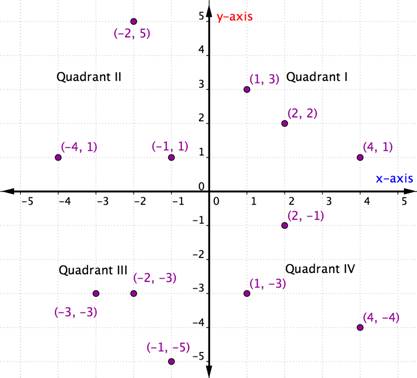
A graph with many plotted points in different quadrants. Quadrant 1 has the point (1,3); the point (2,2); and the point (4,1). Quadrant 2 has the point negative 1, one; the point negative 2, 5; and the point negative 4, one. Quadrant 3 has the point negative 2, negative 3; the point negative 3, negative 3; and the point negative 1, negative 5. Quadrant 4 has the point 2, negative 1; the point 1, negative 3; and the point 4, negative 4.

Figure 4. Points within quadrants.

Within each quadrant, the signs of the [latex]x-[/latex]coordinates and [latex]y-[/latex]coordinates of each ordered pair are the same. They follow a pattern, shown in figure 5.

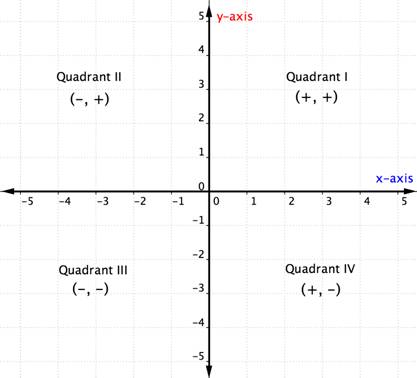
Graph with quadrants. Quadrant 1 is positive, positive. Quadrant 2 is negative, positive. Quadrant 3 is negative, negative. Quadrant 4 is positive, negative.

Figure 5. Patterns of ordered pars within quadrants.

The example below details how to determine the quadrant location of a point just by thinking about the signs of its coordinates. Thinking about the quadrant location before plotting a point can help us prevent mistakes. It is also useful knowledge for checking that we have plotted a point correctly.

Example

In which quadrant is the point [latex](−7,10)[/latex] located?

Example

In which quadrant is the point [latex](−10,−5)[/latex] located?

Solution

Look at the signs of the x- and y-coordinates. For this ordered pair, the signs are [latex](−,−)[/latex].

[latex](−10,−5)[/latex]

Points with the pattern [latex](−,−)[/latex] are in Quadrant III.

Using the table or grid above, locate the pattern [latex](−,−)[/latex].

Answer

The point [latex](−10,−5)[/latex] is in Quadrant III.

Exercises

Plot each point in the rectangular coordinate plane and identify the quadrant in which the point is located:

1. [latex]\left(-1,3\right)[/latex]
2. [latex]\left(-3,-4\right)[/latex]
3. [latex]\left(2,-3\right)[/latex]
4. [latex]\left(3,{\dfrac{5}{2}}\right)[/latex]

Solution

The first number of the coordinate pair is the [latex]x\text{-coordinate}[/latex], and the second number is the [latex]y\text{-coordinate}[/latex].
1. Since [latex]x=-1,y=3[/latex], the point [latex]\left(-1,3\right)[/latex] is in Quadrant II.
2. Since [latex]x=-3,y=-4[/latex], the point [latex]\left(-3,-4\right)[/latex] is in Quadrant III.
3. Since [latex]x=2,y=-1[/latex], the point [latex]\left(2,-1\right)[/latex] is in Quadrant lV.
4. Since [latex]x=3,y={\dfrac{5}{2}}[/latex], the point [latex]\left(3,{\dfrac{5}{2}}\right)[/latex] is in Quadrant I. It may be helpful to write [latex]{\dfrac{5}{2}}[/latex] as the mixed number, [latex]2{\dfrac{1}{2}}[/latex], or decimal, [latex]2.5[/latex]. Then we know that the point is halfway between [latex]2[/latex] and [latex]3[/latex] on the [latex]y\text{-axis}[/latex].

The graph shows the x y-coordinate plane. The x and y-axis each run from -7 to 7. The point

try it

 

Watch the video below to see more examples of how to identify the quadrant that a point is located in.

 Points on the Axes

When a point is plotted on one of the axes, one of the coordinates must be zero. Figure 6 shows the graph of the ordered pair [latex](0,4)[/latex] located on the [latex]y[/latex]-axis.

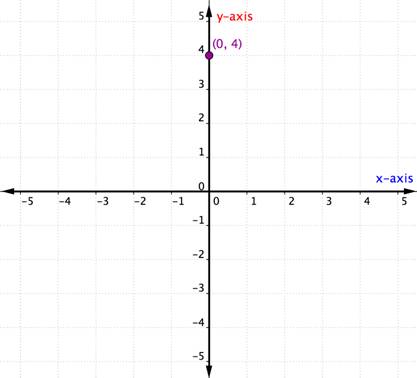
Graph of the point (0,4). The point is on the y-axis.

Figure 6. Plotting a point on the [latex]y[/latex]-axis.

A point located on one of the axes is not considered to be in a quadrant. It is simply on one of the axes. Whenever the [latex]x[/latex]–coordinate is [latex]0[/latex], the point is located on the [latex]y[/latex]–axis. Similarly, any point that has a [latex]y[/latex]–coordinate of [latex]0[/latex] is located on the [latex]x[/latex]–axis.

Points on the Axes

Points with a [latex]y\text{-coordinate}[/latex] equal to [latex]0[/latex] are on the [latex]x\text{-axis}[/latex], and have coordinates [latex]\left(a,0\right)[/latex].

Points with an [latex]x\text{-coordinate}[/latex] equal to [latex]0[/latex] are on the [latex]y\text{-axis}[/latex], and have coordinates [latex]\left(0,b\right)[/latex].

When the point falls on both axes, both coordinates are zero. Therefore, its ordered pair is [latex]\left(0,0\right)[/latex] . This point is called the origin.

The Origin

The point [latex]\left(0,0\right)[/latex] is called the origin. It is the point where the [latex]x[/latex]-axis and [latex]y[/latex]-axis intersect.

ExAMPLE

Plot each point on a coordinate plane:

1. [latex]\left(0,5\right)[/latex]
2. [latex]\left(4,0\right)[/latex]
3. [latex]\left(-3,0\right)[/latex]
4. [latex]\left(0,0\right)[/latex]
5. [latex]\left(0,-1\right)[/latex]

Solution

  1. Since [latex]x=0[/latex], the point whose coordinates are [latex]\left(0,5\right)[/latex] is on the [latex]y\text{-axis}[/latex].
  2. Since [latex]y=0[/latex], the point whose coordinates are [latex]\left(4,0\right)[/latex] is on the [latex]x\text{-axis}[/latex].
  3. Since [latex]y=0[/latex], the point whose coordinates are [latex]\left(-3,0\right)[/latex] is on the [latex]x\text{-axis}[/latex].
  4. Since [latex]x=0[/latex] and [latex]y=0[/latex], the point whose coordinates are [latex]\left(0,0\right)[/latex] is the origin.
  5. Since [latex]x=0[/latex], the point whose coordinates are [latex]\left(0,-1\right)[/latex] is on the [latex]y\text{-axis}[/latex].
    The graph shows the x y-coordinate plane. The x and y-axis each run from -7 to 7. The point

TRY IT

In algebra, being able to identify the coordinates of a point shown on a graph is just as important as being able to plot points. To identify the [latex]x[/latex]-coordinate of a point on a graph, read the number on the [latex]x[/latex]-axis directly above or below the point. To identify the [latex]y[/latex]-coordinate of a point, read the number on the [latex]y[/latex]-axis directly to the left or right of the point. Remember, to write the ordered pair using the correct order [latex]\left(x,y\right)[/latex].

Example

Describe the point shown as an ordered pair.

A point that is 2 spaces above the x-axis and 5 spaces to the right of the y-axis.

Solution

Begin at the origin and move along the [latex]x[/latex]–axis. This is the [latex]x[/latex]–coordinate and is written first in the ordered pair.

[latex]\left(5, y\right)[/latex]

Move from 5 up to the ordered pair and read the number on the [latex]y[/latex]–axis. This is the [latex]y[/latex]–coordinate and is written second in the ordered pair.

[latex](5,2)[/latex]

Answer

The point shown as an ordered pair is [latex](5,2)[/latex].

Describing a point shown as an ordered pair

 

example

Name the ordered pair of each point shown:

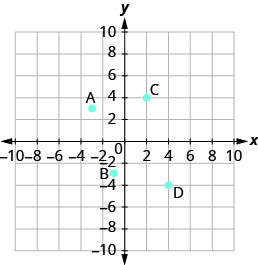
The graph shows the x y-coordinate plane. The x and y-axis each run from -7 to 7. The point

Solution

Point A is above [latex]-3[/latex] on the [latex]x\text{-axis}[/latex], so the [latex]x\text{-coordinate}[/latex] of the point is [latex]-3[/latex]. The point is to the left of [latex]3[/latex] on the [latex]y\text{-axis}[/latex], so the [latex]y\text{-coordinate}[/latex] of the point is [latex]3[/latex]. The coordinates of the point are [latex]\left(-3,3\right)[/latex].

Point B is below [latex]-1[/latex] on the [latex]x\text{-axis}[/latex], so the [latex]x\text{-coordinate}[/latex] of the point is [latex]-1[/latex]. The point is to the left of [latex]-3[/latex] on the [latex]y\text{-axis}[/latex], so the [latex]y\text{-coordinate}[/latex] of the point is [latex]-3[/latex]. The coordinates of the point are [latex]\left(-1,-3\right)[/latex].

Point C is above [latex]2[/latex] on the [latex]x\text{-axis}[/latex], so the [latex]x\text{-coordinate}[/latex] of the point is [latex]2[/latex]. The point is to the right of [latex]4[/latex] on the [latex]y\text{-axis}[/latex], so the [latex]y\text{-coordinate}[/latex] of the point is [latex]4[/latex]. The coordinates of the point are [latex]\left(2,4\right)[/latex].

Point D is below [latex]4[/latex] on the [latex]x-\text{axis}[/latex], so the [latex]x\text{-coordinate}[/latex] of the point is [latex]4[/latex]. The point is to the right of [latex]-4[/latex] on the [latex]y\text{-axis}[/latex], so the [latex]y\text{-coordinate}[/latex] of the point is [latex]-4[/latex]. The coordinates of the point are [latex]\left(4,-4\right)[/latex].

try it

try it

 

Watch the following video for another example of how to determine the ordered pair for points on the coordinate plane.