Distance in the Coordinate Plane

Learning Outcomes

Use the distance formula to find the distance between two points in the plane.
Use the midpoint formula to find the midpoint between two points.

Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. The Pythagorean Theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], is based on a right triangle where a and b are the lengths of the legs adjacent to the right angle, and c is the length of the hypotenuse.

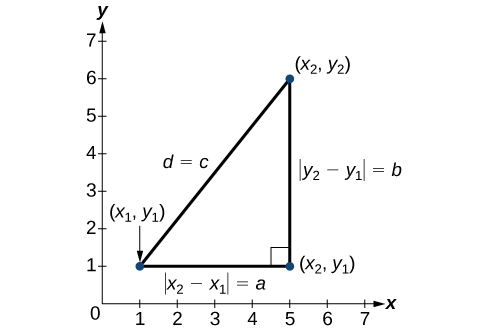
The relationship of sides [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] to side d is the same as that of sides a and b to side c. We use the absolute value symbol to indicate that the length is a positive number because the absolute value of any number is positive. (For example, [latex]|-3|=3[/latex]. ) The symbols [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] indicate that the lengths of the sides of the triangle are positive. To find the length c, take the square root of both sides of the Pythagorean Theorem.

[latex]{c}^{2}={a}^{2}+{b}^{2}\rightarrow c=\sqrt{{a}^{2}+{b}^{2}}[/latex]

It follows that the distance formula is given as

[latex]{d}^{2}={\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}\to d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]

We do not have to use the absolute value symbols in this definition because any number squared is positive.

A General Note: The Distance Formula

Given endpoints [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the distance between two points is given by

[latex]d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]

Example: Finding the Distance between Two Points

Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].

Show Solution

Try It

Find the distance between two points: [latex]\left(1,4\right)[/latex] and [latex]\left(11,9\right)[/latex].

Show Show Solution

In the following video, we present more worked examples of how to use the distance formula to find the distance between two points in the coordinate plane.

Example: Finding the Distance between Two Locations

Let’s return to the situation introduced at the beginning of this section.

Tracie set out from Elmhurst, IL to go to Franklin Park. On the way, she made a few stops to do errands. Each stop is indicated by a red dot. Find the total distance that Tracie traveled. Compare this with the distance between her starting and final positions.

Show Solution

The first thing we should do is identify ordered pairs to describe each position. If we set the starting position at the origin, we can identify each of the other points by counting units east (right) and north (up) on the grid. For example, the first stop is 1 block east and 1 block north, so it is at [latex]\left(1,1\right)[/latex]. The next stop is 5 blocks to the east so it is at [latex]\left(5,1\right)[/latex]. After that, she traveled 3 blocks east and 2 blocks north to [latex]\left(8,3\right)[/latex]. Lastly, she traveled 4 blocks north to [latex]\left(8,7\right)[/latex]. We can label these points on the grid.

This is an image of a road map of a city. The point (1, 1) is on North Avenue and Bertau Avenue. The point (5, 1) is on North Avenue and Wolf Road. The point (8, 3) is on Mannheim Road and McLean Street. The point (8, 7) is on Mannheim Road and Schiller Avenue.

Next, we can calculate the distance. Note that each grid unit represents 1,000 feet.

From her starting location to her first stop at [latex]\left(1,1\right)[/latex], Tracie might have driven north 1,000 feet and then east 1,000 feet, or vice versa. Either way, she drove 2,000 feet to her first stop.
Her second stop is at [latex]\left(5,1\right)[/latex]. So from [latex]\left(1,1\right)[/latex] to [latex]\left(5,1\right)[/latex], Tracie drove east 4,000 feet.
Her third stop is at [latex]\left(8,3\right)[/latex]. There are a number of routes from [latex]\left(5,1\right)[/latex] to [latex]\left(8,3\right)[/latex]. Whatever route Tracie decided to use, the distance is the same, as there are no angular streets between the two points. Let’s say she drove east 3,000 feet and then north 2,000 feet for a total of 5,000 feet.
Tracie’s final stop is at [latex]\left(8,7\right)[/latex]. This is a straight drive north from [latex]\left(8,3\right)[/latex] for a total of 4,000 feet.

Next, we will add the distances listed in the table.

From/To	Number of Feet Driven
[latex]\left(0,0\right)[/latex] to [latex]\left(1,1\right)[/latex]	2,000
[latex]\left(1,1\right)[/latex] to [latex]\left(5,1\right)[/latex]	4,000
[latex]\left(5,1\right)[/latex] to [latex]\left(8,3\right)[/latex]	5,000
[latex]\left(8,3\right)[/latex] to [latex]\left(8,7\right)[/latex]	4,000
Total	15,000

The total distance Tracie drove is 15,000 feet or 2.84 miles. This is not, however, the actual distance between her starting and ending positions. To find this distance, we can use the distance formula between the points [latex]\left(0,0\right)[/latex] and [latex]\left(8,7\right)[/latex].

[latex]\begin{array}{l}d=\sqrt{{\left(8 - 0\right)}^{2}+{\left(7 - 0\right)}^{2}}\hfill \\ =\sqrt{64+49}\hfill \\ =\sqrt{113}\hfill \\ =10.63\text{ units}\hfill \end{array}[/latex]

At 1,000 feet per grid unit, the distance between Elmhurst, IL to Franklin Park is 10,630.14 feet, or 2.01 miles. The distance formula results in a shorter calculation because it is based on the hypotenuse of a right triangle, a straight diagonal from the origin to the point [latex]\left(8,7\right)[/latex]. Perhaps you have heard the saying “as the crow flies,” which means the shortest distance between two points because a crow can fly in a straight line even though a person on the ground has to travel a longer distance on existing roadways.

Using the Midpoint Formula

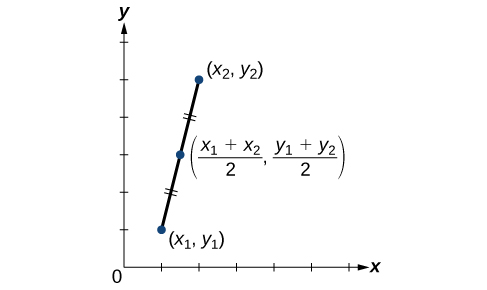
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula. Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint formula states how to find the coordinates of the midpoint [latex]M[/latex].

[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]

A graphical view of a midpoint is shown below. Notice that the line segments on either side of the midpoint are congruent.

This is a line graph on an x, y coordinate plane with the x and y axes ranging from 0 to 6. The points (x sub 1, y sub 1), (x sub 2, y sub 2), and (x sub 1 plus x sub 2 all over 2, y sub 1 plus y sub 2 all over 2) are plotted. A straight line runs through these three points. Pairs of short parallel lines bisect the two sections of the line to note that they are equivalent.

Example: Finding the Midpoint of the Line Segment

Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].

Show Solution

Try It

Find the midpoint of the line segment with endpoints [latex]\left(-2,-1\right)[/latex] and [latex]\left(-8,6\right)[/latex].

Show Solution

Example: Finding the Center of a Circle

The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.

Show Solution

Try It

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this page Learn More

Module 3: The Rectangular Coordinate System and Equations of Lines