Learning Outcomes
- Draw the graph of a polynomial function using end behavior, turning points, intercepts, and the Intermediate Value Theorem.
We can use what we have learned about multiplicities, end behavior, and turning points to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.
How To: Given a polynomial function, sketch the graph
- Find the intercepts.
- Check for symmetry. If the function is an even function, its graph is symmetric with respect to the y-axis, that is, f(–x) = f(x).
If a function is an odd function, its graph is symmetric with respect to the origin, that is, f(–x) = –f(x). - Use the multiplicities of the zeros to determine the behavior of the polynomial at the x-intercepts.
- Determine the end behavior by examining the leading term.
- Use the end behavior and the behavior at the intercepts to sketch the graph.
- Ensure that the number of turning points does not exceed one less than the degree of the polynomial.
- Optionally, use technology to check the graph.
Example: Sketching the Graph of a Polynomial Function
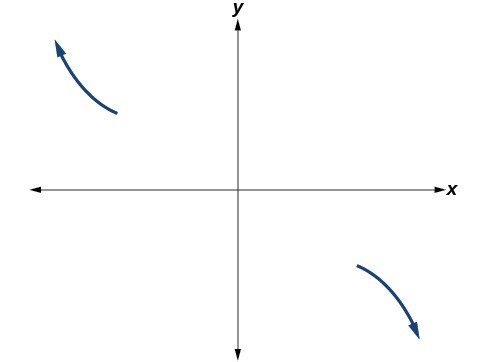
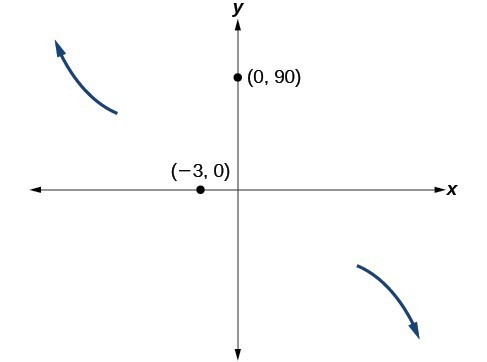
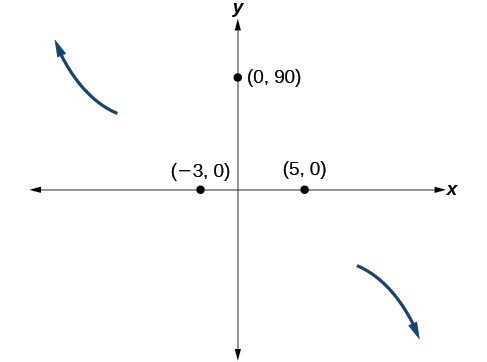
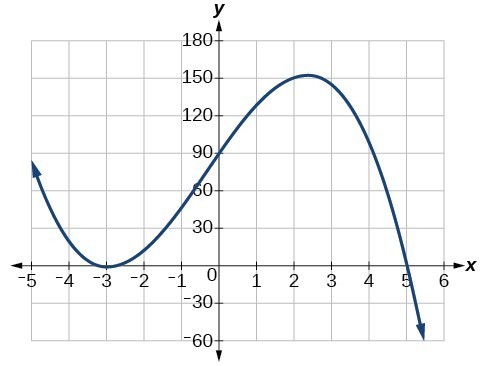
Sketch a possible graph for [latex]f\left(x\right)=-2{\left(x+3\right)}^{2}\left(x - 5\right)[/latex].
Try It
Sketch a possible graph for [latex]f\left(x\right)=\frac{1}{4}x{\left(x - 1\right)}^{4}{\left(x+3\right)}^{3}[/latex].
Check yourself with an online graphing tool when you are done.
Try it
Use an online graphing tool to find an odd degree function with one zero at (-3,0) whose multiplicity is 3 and another zero at (2,0) with multiplicity 2. The end behavior of the graph is:
as [latex]x\rightarrow-\infty, f(x) \rightarrow\infty[/latex] and as [latex]x\rightarrow \infty, f(x)\rightarrow -\infty[/latex]
The Intermediate Value Theorem
In some situations, we may know two points on a graph but not the zeros. If those two points are on opposite sides of the x-axis, we can confirm that there is a zero between them. Consider a polynomial function f whose graph is smooth and continuous. The Intermediate Value Theorem states that for two numbers a and b in the domain of f, if a < b and [latex]f\left(a\right)\ne f\left(b\right)[/latex], then the function f takes on every value between [latex]f\left(a\right)[/latex] and [latex]f\left(b\right)[/latex].
We can apply this theorem to a special case that is useful for graphing polynomial functions. If a point on the graph of a continuous function f at [latex]x=a[/latex] lies above the x-axis and another point at [latex]x=b[/latex] lies below the x-axis, there must exist a third point between [latex]x=a[/latex] and [latex]x=b[/latex] where the graph crosses the x-axis. Call this point [latex]\left(c,\text{ }f\left(c\right)\right)[/latex]. This means that we are assured there is a value c where [latex]f\left(c\right)=0[/latex].
In other words, the Intermediate Value Theorem tells us that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis. The figure below shows that there is a zero between a and b.
The Intermediate Value Theorem can be used to show there exists a zero.
A General Note: Intermediate Value Theorem
Let f be a polynomial function. The Intermediate Value Theorem states that if [latex]f\left(a\right)[/latex] and [latex]f\left(b\right)[/latex] have opposite signs, then there exists at least one value c between a and b for which [latex]f\left(c\right)=0[/latex].
Example: Using the Intermediate Value Theorem
Show that the function [latex]f\left(x\right)={x}^{3}-5{x}^{2}+3x+6[/latex] has at least two real zeros between [latex]x=1[/latex] and [latex]x=4[/latex].
Try It
Show that the function [latex]f\left(x\right)=7{x}^{5}-9{x}^{4}-{x}^{2}[/latex] has at least one real zero between [latex]x=1[/latex] and [latex]x=2[/latex].
