Learning Outcomes
- Graph a rational function using intercepts, asymptotes, and end behavior.
- Write a rational function given intercepts and asymptotes.
Previously we saw that the numerator of a rational function reveals the [latex]x[/latex]-intercepts of the graph, whereas the denominator reveals the vertical asymptotes of the graph. As with polynomials, factors of the numerator may have integer powers greater than one. Fortunately, the effect on the shape of the graph at those intercepts is the same as we saw with polynomials.
The vertical asymptotes associated with the factors of the denominator will mirror one of the two toolkit reciprocal functions. When the degree of the factor in the denominator is odd, the distinguishing characteristic is that on one side of the vertical asymptote the graph heads towards positive infinity, and on the other side the graph heads towards negative infinity.
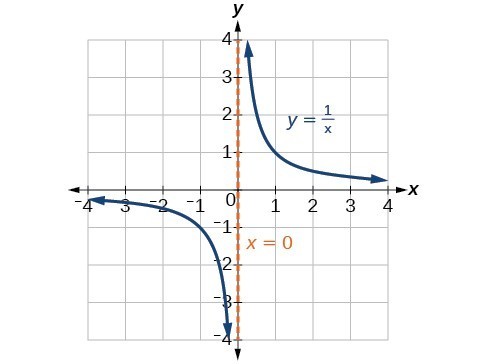
When the degree of the factor in the denominator is even, the distinguishing characteristic is that the graph either heads toward positive infinity on both sides of the vertical asymptote or heads toward negative infinity on both sides.
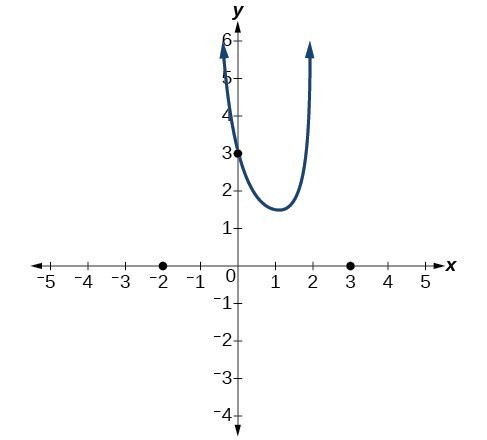
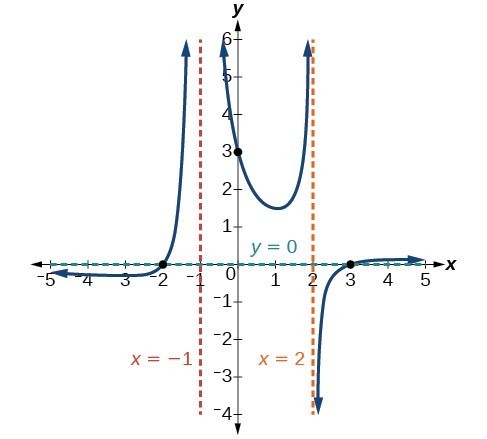
For example the graph of [latex]f\left(x\right)=\dfrac{{\left(x+1\right)}^{2}\left(x - 3\right)}{{\left(x+3\right)}^{2}\left(x - 2\right)}[/latex].
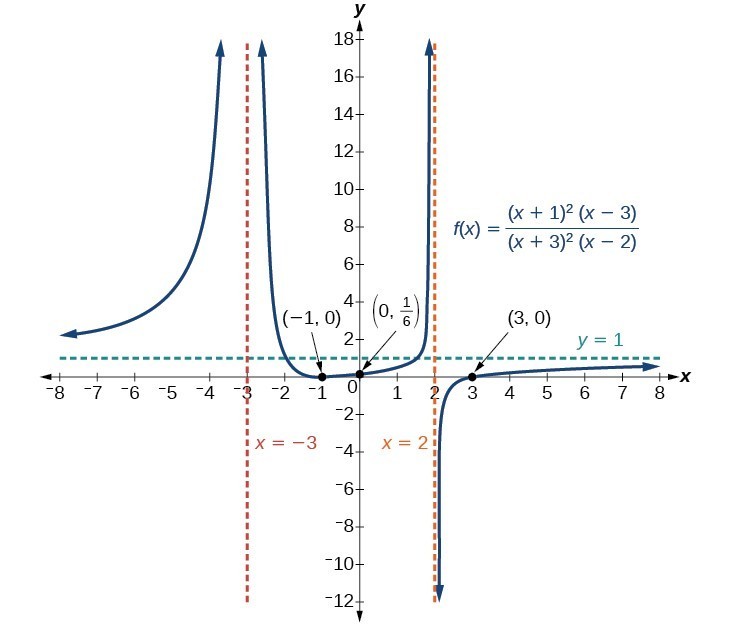
- At the [latex]x[/latex]-intercept [latex]x=-1[/latex] corresponding to the [latex]{\left(x+1\right)}^{2}[/latex] factor of the numerator, the graph bounces, consistent with the quadratic nature of the factor.
- At the [latex]x[/latex]-intercept [latex]x=3[/latex] corresponding to the [latex]\left(x - 3\right)[/latex] factor of the numerator, the graph passes through the axis as we would expect from a linear factor.
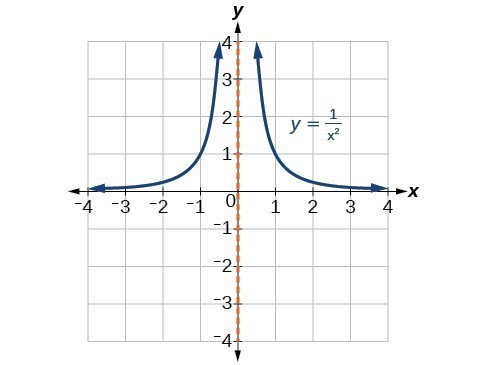
- At the vertical asymptote [latex]x=-3[/latex] corresponding to the [latex]{\left(x+3\right)}^{2}[/latex] factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex].
- At the vertical asymptote [latex]x=2[/latex], corresponding to the [latex]\left(x - 2\right)[/latex] factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side, consistent with the behavior of the function [latex]f\left(x\right)=\frac{1}{x}[/latex].
How To: Given a rational function, sketch a graph.
- Evaluate the function at 0 to find the y-intercept.
- Factor the numerator and denominator.
- For factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the [latex]x[/latex]-intercepts.
- Find the multiplicities of the [latex]x[/latex]-intercepts to determine the behavior of the graph at those points.
- For factors in the denominator, note the multiplicities of the zeros to determine the local behavior. For those factors not common to the numerator, find the vertical asymptotes by setting those factors equal to zero and then solve.
- For factors in the denominator common to factors in the numerator, find the removable discontinuities by setting those factors equal to 0 and then solve.
- Compare the degrees of the numerator and the denominator to determine the horizontal or slant asymptotes.
- Sketch the graph.
Example: Graphing a Rational Function
Sketch a graph of [latex]f\left(x\right)=\dfrac{\left(x+2\right)\left(x - 3\right)}{{\left(x+1\right)}^{2}\left(x - 2\right)}[/latex].
Try It
Given the function [latex]f\left(x\right)=\dfrac{{\left(x+2\right)}^{2}\left(x - 2\right)}{2{\left(x - 1\right)}^{2}\left(x - 3\right)}[/latex], use the characteristics of polynomials and rational functions to describe its behavior and sketch the function.
![]()
Watch the following video to see another worked example of how to match different kinds of rational functions with their graphs.
Writing Rational Functions
Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an [latex]x[/latex]-intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of [latex]x[/latex]-intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.
A General Note: Writing Rational Functions from Intercepts and Asymptotes
If a rational function has [latex]x[/latex]-intercepts at [latex]x={x}_{1}, {x}_{2}, ..., {x}_{n}[/latex], vertical asymptotes at [latex]x={v}_{1},{v}_{2},\dots ,{v}_{m}[/latex], and no [latex]{x}_{i}=\text{any }{v}_{j}[/latex], then the function can be written in the form:
[latex]f\left(x\right)=a\frac{{\left(x-{x}_{1}\right)}^{{p}_{1}}{\left(x-{x}_{2}\right)}^{{p}_{2}}\cdots {\left(x-{x}_{n}\right)}^{{p}_{n}}}{{\left(x-{v}_{1}\right)}^{{q}_{1}}{\left(x-{v}_{2}\right)}^{{q}_{2}}\cdots {\left(x-{v}_{m}\right)}^{{q}_{n}}}[/latex]
where the powers [latex]{p}_{i}[/latex] or [latex]{q}_{i}[/latex] on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor [latex]a[/latex] can be determined given a value of the function other than the [latex]x[/latex]-intercept or by the horizontal asymptote if it is nonzero.
How To: Given a graph of a rational function, write the function.
- Determine the factors of the numerator. Examine the behavior of the graph at the x-intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the “simplest” function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
- Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
- Use any clear point on the graph to find the stretch factor.
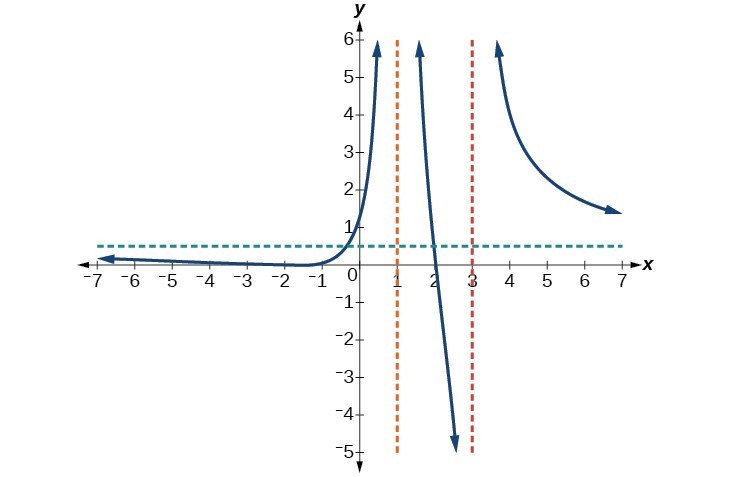
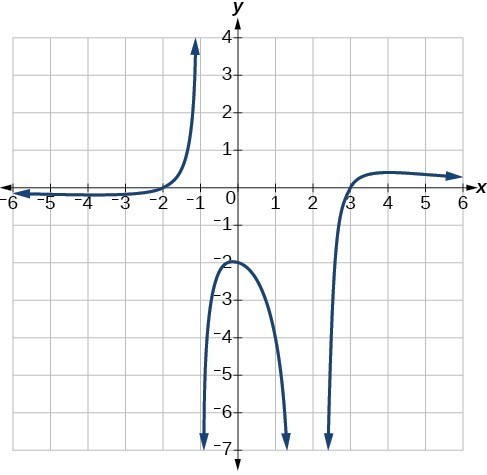
Example: Writing a Rational Function from Intercepts and Asymptotes
Write an equation for the rational function below.
Contribute!
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 1802. Authored by: Lippman,David. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 129075. Authored by: Day, Alyson. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex: Match Equations of Rational Functions to Graphs . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/vMVYaFptvkk. License: CC BY: Attribution