Introduction to Polynomial Basics

What you’ll learn to do: Create and evaluate expressions involving polynomials

Earl is building a doghouse whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which the dog can enter and exit the house. Earl wants to find the area of the front of the doghouse so that he can purchase the correct amount of paint. Using the measurements of the front of the house shown below, we can create an expression that combines several variable terms which allows us to solve this problem and others like it.

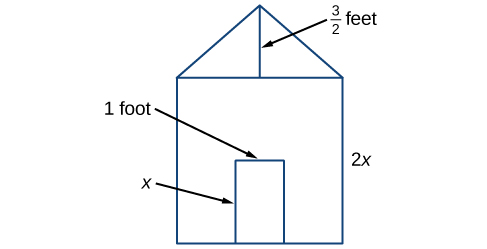
Sketch of a house formed by a square and a triangle based on the top of the square. A rectangle is placed at the bottom center of the square to mark a doorway. The height of the door is labeled: x and the width of the door is labeled: 1 foot. The side of the square is labeled: 2x. The height of the triangle is labeled: 3/2 feet.

Measurements of the front of the doghouse Earl is building.

First, find the area of the square in square feet.

[latex]\begin{array}{ccc}\hfill A& =& {s}^{2}\hfill \\ & =& {\left(2x\right)}^{2}\hfill \\ & =& 4{x}^{2}\hfill \end{array}[/latex]

Then, find the area of the triangle in square feet.

[latex]\begin{array}{ccc}\hfill A& =& \frac{1}{2}bh\hfill \\ & =& \text{}\frac{1}{2}\left(2x\right)\left(\frac{3}{2}\right)\hfill \\ & =& \text{}\frac{3}{2}x\hfill \end{array}[/latex]

Next, find the area of the rectangular door in square feet.

[latex]\begin{array}{ccc}\hfill A& =& lw\hfill \\ & =& x\cdot 1\hfill \\ \hfill & =& x\hfill \end{array}[/latex]

The area of the front of the doghouse can be found by adding the areas of the square and the triangle and then subtracting the area of the rectangle. When we do this, we get [latex]4{x}^{2}+\frac{3}{2}x-x[/latex] ft2, or [latex]4{x}^{2}+\frac{1}{2}x[/latex] ft2.

In this module, we will examine expressions such as this one which combine several variable terms.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this pageLearn More