Stretching, Compressing, or Reflecting an Exponential Function

Learning Outcomes

  • Graph a stretched or compressed exponential function.
  • Graph a reflected exponential function.
  • Write the equation of an exponential function that has been transformed.

While horizontal and vertical shifts involve adding constants to the input or to the function itself, a stretch or compression occurs when we multiply the parent function [latex]f\left(x\right)={b}^{x}[/latex] by a constant [latex]|a|>0[/latex]. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph the stretch, using [latex]a=3[/latex], to get [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] and the compression, using [latex]a=\frac{1}{3}[/latex], to get [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex].

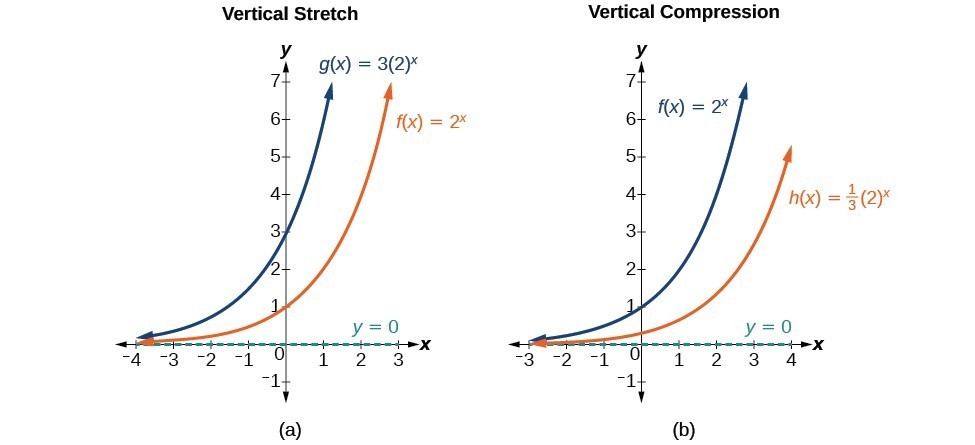
Two graphs where graph a is an example of vertical stretch and graph b is an example of vertical compression.

(a) [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] stretches the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of 3. (b) [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex] compresses the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of [latex]\frac{1}{3}[/latex].

A General Note: Stretches and Compressions of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]

The function [latex]f\left(x\right)=a{b}^{x}[/latex]

  • is stretched vertically by a factor of a if [latex]|a|>1[/latex].
  • is compressed vertically by a factor of a if [latex]|a|<1[/latex].
  • has a y-intercept is [latex]\left(0,a\right)[/latex].
  • has a horizontal asymptote of [latex]y=0[/latex], range of [latex]\left(0,\infty \right)[/latex], and domain of [latex]\left(-\infty ,\infty \right)[/latex] which are all unchanged from the parent function.

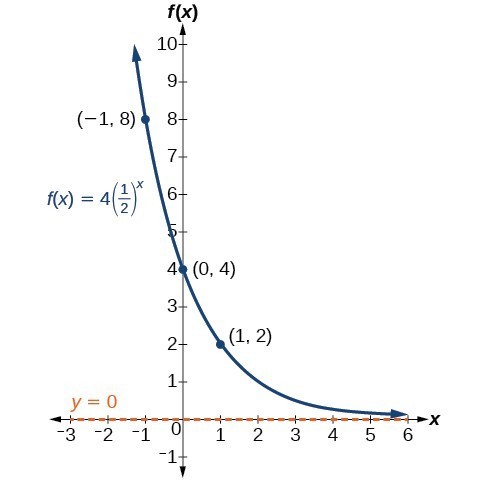
Example: Graphing the Stretch of an Exponential Function

Sketch a graph of [latex]f\left(x\right)=4{\left(\frac{1}{2}\right)}^{x}[/latex]. State the domain, range, and asymptote.

Try It

Graphing Reflections

In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x-axis or the y-axis. When we multiply the parent function [latex]f\left(x\right)={b}^{x}[/latex] by –1, we get a reflection about the x-axis. When we multiply the input by –1, we get a reflection about the y-axis. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph the two reflections alongside it. The reflection about the x-axis, [latex]g\left(x\right)={-2}^{x}[/latex], and the reflection about the y-axis, [latex]h\left(x\right)={2}^{-x}[/latex], are both shown below.

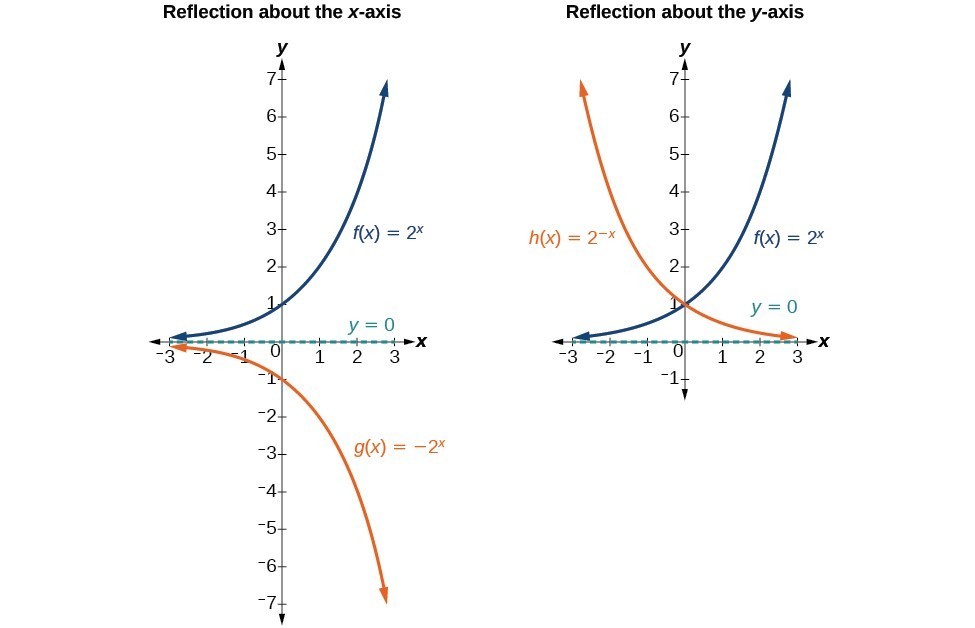
Two graphs where graph a is an example of a reflection about the x-axis and graph b is an example of a reflection about the y-axis.

(a) [latex]g\left(x\right)=-{2}^{x}[/latex] reflects the graph of [latex]f\left(x\right)={2}^{x}[/latex] about the x-axis. (b) [latex]h\left(x\right)={2}^{-x}[/latex] reflects the graph of [latex]f\left(x\right)={2}^{x}[/latex] about the y-axis.

A General Note: Reflecting the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]

The function [latex]f\left(x\right)=-{b}^{x}[/latex]

  • reflects the parent function [latex]f\left(x\right)={b}^{x}[/latex] about the x-axis.
  • has a y-intercept of [latex]\left(0,-1\right)[/latex].
  • has a range of [latex]\left(-\infty ,0\right)[/latex].
  • has a horizontal asymptote of [latex]y=0[/latex] and domain of [latex]\left(-\infty ,\infty \right)[/latex] which are unchanged from the parent function.

The function [latex]f\left(x\right)={b}^{-x}[/latex]

  • reflects the parent function [latex]f\left(x\right)={b}^{x}[/latex] about the y-axis.
  • has a y-intercept of [latex]\left(0,1\right)[/latex], a horizontal asymptote at [latex]y=0[/latex], a range of [latex]\left(0,\infty \right)[/latex], and a domain of [latex]\left(-\infty ,\infty \right)[/latex] which are unchanged from the parent function.

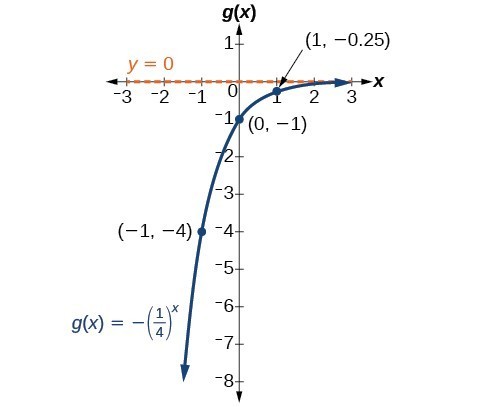
Example: Writing and Graphing the Reflection of an Exponential Function

Find and graph the equation for a function, [latex]g\left(x\right)[/latex], that reflects [latex]f\left(x\right)={\left(\frac{1}{4}\right)}^{x}[/latex] about the x-axis. State its domain, range, and asymptote.

Summarizing Transformations of the Exponential Function

Now that we have worked with each type of translation for the exponential function, we can summarize them to arrive at the general equation for transforming exponential functions.

Transformations of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]
Translation Form
Shift

  • Horizontally c units to the left
  • Vertically d units up
 [latex]f\left(x\right)={b}^{x+c}+d[/latex]
Stretch and Compress

  • Stretch if |a|>1
  • Compression if 0<|a|<1
 [latex]f\left(x\right)=a{b}^{x}[/latex]
Reflect about the x-axis [latex]f\left(x\right)=-{b}^{x}[/latex]
Reflect about the y-axis [latex]f\left(x\right)={b}^{-x}={\left(\frac{1}{b}\right)}^{x}[/latex]
General equation for all transformations [latex]f\left(x\right)=a{b}^{x+c}+d[/latex]

A General Note: Transformations of Exponential Functions

A transformation of an exponential function has the form

[latex]f\left(x\right)=a{b}^{x+c}+d[/latex], where the parent function, [latex]y={b}^{x}[/latex], [latex]b>1[/latex], is

  • shifted horizontally c units to the left.
  • stretched vertically by a factor of |a| if |a| > 0.
  • compressed vertically by a factor of |a| if 0 < |a| < 1.
  • shifted vertically d units.
  • reflected about the x-axis when a < 0.

Note the order of the shifts, transformations, and reflections follow the order of operations.

Example: Writing a Function from a Description

Write the equation for the function described below. Give the horizontal asymptote, domain, and range.

  • [latex]f\left(x\right)={e}^{x}[/latex] is vertically stretched by a factor of 2, reflected across the y-axis, and then shifted up 4 units.

Try It

Write the equation for the function described below. Give the horizontal asymptote, the domain, and the range.

  • [latex]f\left(x\right)={e}^{x}[/latex] is compressed vertically by a factor of [latex]\frac{1}{3}[/latex], reflected across the x-axis, and then shifted down 2 units.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this pageLearn More